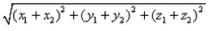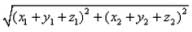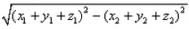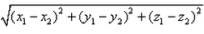All Exams >
Commerce >
Mathematics (Maths) Class 11 >
All Questions
All questions of Introduction to Three Dimensional Geometry for Commerce Exam
The point (1, – 2, – 3) lies in
- a)7th octant
- b)5th octant
- c)6th octant
- d)8th octant
Correct answer is option 'D'. Can you explain this answer?
The point (1, – 2, – 3) lies in
a)
7th octant
b)
5th octant
c)
6th octant
d)
8th octant
|
Poonam Reddy answered |
The eight octants can be divided into 2 parts.
Positive direction of Z-axis and negative direction of Z-axis.
Thus we have 2 sets of co-ordinates:
(+, +, +) ; (+, -, +) ; (-, +, +) ; (-, -, +)
(+, +, -) ; (+, -, -) ; (-, +, -) ; (-, -, -)
Therefore, the points (1,-2,-3) lies in 8th octant.
Positive direction of Z-axis and negative direction of Z-axis.
Thus we have 2 sets of co-ordinates:
(+, +, +) ; (+, -, +) ; (-, +, +) ; (-, -, +)
(+, +, -) ; (+, -, -) ; (-, +, -) ; (-, -, -)
Therefore, the points (1,-2,-3) lies in 8th octant.
The image of (–2, 3, 4) in the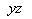 
-plane is:- a)(0, 3, 4)
- b)(2, 3, 4)
- c)(2, 0, 0)
- d)(– 2, 0, 0)
Correct answer is option 'B'. Can you explain this answer?
The image of (–2, 3, 4) in the 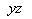-plane is:
-plane is:a)
(0, 3, 4)
b)
(2, 3, 4)
c)
(2, 0, 0)
d)
(– 2, 0, 0)
|
Raghav Bansal answered |
The image of(-2,3,4) reflects in the 1st quadrant. As we know that in 1st quadrant all the x,y and z are positive
So the resultant will be : (2,3,4)
So the resultant will be : (2,3,4)
The image of point (5, 2, – 7) in XY plane is:
- a) (- 5, 2, -7)
- b) (- 5, – 2, 7)
- c) (5, 2, 7)
- d) (5, 2, – 7)
Correct answer is option 'C'. Can you explain this answer?
The image of point (5, 2, – 7) in XY plane is:
a)
(- 5, 2, -7)b)
(- 5, – 2, 7)c)
(5, 2, 7)d)
(5, 2, – 7)|
|
Poonam Reddy answered |
Given: Point is (5, 2, -7)
To find: the image of the point in xy-plane
To find: the image of the point in xy-plane
Since we need to find its image in xy-plane, a sign of its z-coordinate will change
So, Image of point (5, 2, -7) is (5, 2, 7)
So, Image of point (5, 2, -7) is (5, 2, 7)
If the origin is the centroid of the triangle ABC with vertices A (2a, 14, 6), B (8, 3b, -10) and C(-4, 2, 2c), then the values of a and c are.- a)2 and -2
- b)-2 and 2
- c)1/2 and 1/2
- d)
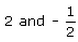
Correct answer is option 'B'. Can you explain this answer?
If the origin is the centroid of the triangle ABC with vertices A (2a, 14, 6), B (8, 3b, -10) and C(-4, 2, 2c), then the values of a and c are.
a)
2 and -2
b)
-2 and 2
c)
1/2 and 1/2
d)
|
Aryan Khanna answered |
The coordinates of the centroid of △ABC
=[(2a−8+4)/3 , (3b+14+2)0/3 , (6−10+2c)/3]
=[(2a-4)/3 , (3b+16)/3 , (2c−4)/3]
It is given that origin is the centroid of △ABC
∴ (0,0,0)=[(2a+4)/3 , (3b+16)/3 , (2c−4)/3]
(2a+4)/3 = 0 , (3b+16)/3 = 0and (2c−4)/3 = 0
⇒ a=−2 and c=2
=[(2a−8+4)/3 , (3b+14+2)0/3 , (6−10+2c)/3]
=[(2a-4)/3 , (3b+16)/3 , (2c−4)/3]
It is given that origin is the centroid of △ABC
∴ (0,0,0)=[(2a+4)/3 , (3b+16)/3 , (2c−4)/3]
(2a+4)/3 = 0 , (3b+16)/3 = 0and (2c−4)/3 = 0
⇒ a=−2 and c=2
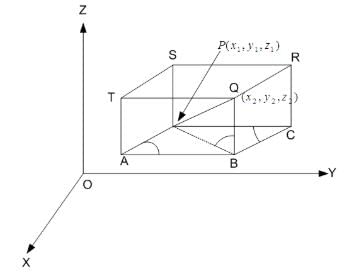
The coordinates of the point R which divides the line segment joining two points P (x1, y1, z1) and Q (x2, y2, z2) externally in the ratio m : n are given by- a)
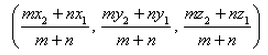
- b)
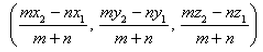
- c)
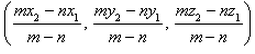
- d)
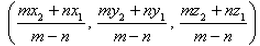
Correct answer is option 'C'. Can you explain this answer?
The coordinates of the point R which divides the line segment joining two points P (x1, y1, z1) and Q (x2, y2, z2) externally in the ratio m : n are given by
a)
b)
c)
d)
|
Pioneer Academy answered |
Using section formula
The coordinates of point R that divides the line segment joining points P (x1, y1, z1) and Q (x2, y2, z2) externally in the ratio m: n are .
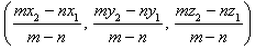
The coordinates of point R that divides the line segment joining points P (x1, y1, z1) and Q (x2, y2, z2) externally in the ratio m: n are .
A and B be the points (3, 4, 5) and (-1, -3, -7), respectively, the equation of the set of points P such that PA2 + PB2 = k2, where k is a constant will- a)Have a term of k to the power 1 only
- b)Have a term of k to the power 2 only
- c)Have a term of k to the power 1 and another with k to the power 2
- d)Be independent of k
Correct answer is option 'B'. Can you explain this answer?
A and B be the points (3, 4, 5) and (-1, -3, -7), respectively, the equation of the set of points P such that PA2 + PB2 = k2, where k is a constant will
a)
Have a term of k to the power 1 only
b)
Have a term of k to the power 2 only
c)
Have a term of k to the power 1 and another with k to the power 2
d)
Be independent of k
|
|
Ravanlein Sekho answered |
D
The point (2, – 2, 3) lies in- a)7th octant
- b)6th octant
- c)4th octant
- d)3rd octant
Correct answer is option 'C'. Can you explain this answer?
The point (2, – 2, 3) lies in
a)
7th octant
b)
6th octant
c)
4th octant
d)
3rd octant
|
|
Aryan Khanna answered |
In the 3D, fourth quadrant has x positive, y negative and z positive.
The distance of the point (3, 4, 5) from X-axis is:- a)√41
- b)7
- c)2√11
- d)5√2
Correct answer is option 'A'. Can you explain this answer?
The distance of the point (3, 4, 5) from X-axis is:
a)
√41
b)
7
c)
2√11
d)
5√2
|
|
Sounak Yadav answered |
The distance of a point from the X-axis can be found by calculating the absolute value of its y-coordinate and z-coordinate.
In this case, the y-coordinate of the point is 4 and the z-coordinate is 5.
So, the distance of the point (3, 4, 5) from the X-axis is |4| + |5| = 4 + 5 = 9.
In this case, the y-coordinate of the point is 4 and the z-coordinate is 5.
So, the distance of the point (3, 4, 5) from the X-axis is |4| + |5| = 4 + 5 = 9.
The coordinates of the centroid of a triangle whose vertices are (2, –1, 6), (3, 3, –2) and (–2, 1, –1) are:- a)(1, 1, 1)
- b)
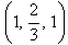
- c)
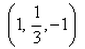
- d)
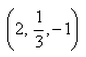
Correct answer is option 'A'. Can you explain this answer?
The coordinates of the centroid of a triangle whose vertices are (2, –1, 6), (3, 3, –2) and (–2, 1, –1) are:
a)
(1, 1, 1)
b)
c)
d)
|
Reena Dhanesh Kumar answered |
Eqn for finding centroid is (x1+x2+x2 ,y1+y2+y3, z1+z2+z3)
apply this formula you'll get the answer
apply this formula you'll get the answer
In which plane does the point (-3, -6, 0) lie?- a)XY and YZ planes
- b)XZ plane
- c)XY plane
- d)YZ plane
Correct answer is option 'C'. Can you explain this answer?
In which plane does the point (-3, -6, 0) lie?
a)
XY and YZ planes
b)
XZ plane
c)
XY plane
d)
YZ plane
|
|
Aryan Khanna answered |
In this question, the ��-coordinate is negative three, the ��-coordinate is negative six, and the ��-coordinate is zero. As �� is equal to zero, the point will not move in the direction of the ��-axis. We can therefore conclude that as �� is equal to zero, the point will lie on the ����-plane. If our ��-coordinate was equal to zero but �� and �� had a positive or negative value, the point would lie in the ����-plane.
If the origin is the centroid of the triangle PQR with vertices P(2a, 2, 6), Q(-4, 3b, -10) and (8, 14, 2c), then the values of a, b and c are:
- a)
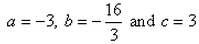
- b)
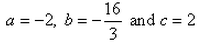
- c)
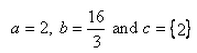
- d)
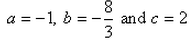
Correct answer is option 'B'. Can you explain this answer?
If the origin is the centroid of the triangle PQR with vertices P(2a, 2, 6), Q(-4, 3b, -10) and (8, 14, 2c), then the values of a, b and c are:
a)
b)
c)
d)
|
Lavanya Menon answered |
The coordinates of the centroid of △PQR
=[(2a−4+8)/3 , (2+3b+14)/3 , (6−10+2c)/3] =((2a+4)/3, (3b+16)/3 ,(2c−4)/3)
It is given that origin is the centroid of △PQR
∴ (0,0,0)=((2a+4)/3, (3b+16)/3, (2c−4)/3)
⇒ (2a+4)/3 =0, (3b+16)/3 = 0 and (2c−4)/3=0
⇒ a =−2,b =−16/3 and c = 2
=[(2a−4+8)/3 , (2+3b+14)/3 , (6−10+2c)/3] =((2a+4)/3, (3b+16)/3 ,(2c−4)/3)
It is given that origin is the centroid of △PQR
∴ (0,0,0)=((2a+4)/3, (3b+16)/3, (2c−4)/3)
⇒ (2a+4)/3 =0, (3b+16)/3 = 0 and (2c−4)/3=0
⇒ a =−2,b =−16/3 and c = 2
Find the points on z-axis which are at a distance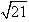 
from the point (1, 2, 3).- a)(0, 0, 7), (0, 0, –1)
- b)(2, 7, 0), (–3, 2, 0)
- c)(1, 7, 0), (4, 3, 0)
- d)(0, 0, –7), (0, 0, 1)
Correct answer is option 'A'. Can you explain this answer?
Find the points on z-axis which are at a distance 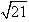from the point (1, 2, 3).
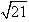from the point (1, 2, 3).a)
(0, 0, 7), (0, 0, –1)
b)
(2, 7, 0), (–3, 2, 0)
c)
(1, 7, 0), (4, 3, 0)
d)
(0, 0, –7), (0, 0, 1)
|
Yash Patel answered |
Let the point on Z axis be given as (0,0,z). The distance between (1,2,3) and (0,0,z) is given as [(1)2 + (2)2 + (3-z)2]½ = (21)1/2
5+(3−z)2=21
z2−6z−7=0
z=7,z = −1
Hence points are (0,0,7),(0,0,−1)
5+(3−z)2=21
z2−6z−7=0
z=7,z = −1
Hence points are (0,0,7),(0,0,−1)
A point has coordinates (0,-3,0), So it lies on the- a)z axis
- b)intersection of x and y axes
- c)y axis
- d)x axis
Correct answer is option 'C'. Can you explain this answer?
A point has coordinates (0,-3,0), So it lies on the
a)
z axis
b)
intersection of x and y axes
c)
y axis
d)
x axis
|
Smrity answered |
As we know coordinate of any point is (x,y,z) . that's why according to question , (x=0 ,y = -3 ,z=0 ) .so it lies on y axis.
The equation representing the set of points which are equidistant from the points (1, 2 , 3) and ( 3 , 2 , -1) is- a)2x – 2y = 0
- b)x – 2y = 0
- c)-x + 2y = 0
- d)x – 2z = 0
Correct answer is option 'D'. Can you explain this answer?
The equation representing the set of points which are equidistant from the points (1, 2 , 3) and ( 3 , 2 , -1) is
a)
2x – 2y = 0
b)
x – 2y = 0
c)
-x + 2y = 0
d)
x – 2z = 0
|
|
Arun Khanna answered |
Let P (x, y, z) be the point that is equidistant from points A(1, 2, 3) and B(3, 2, –1).
Accordingly, PA = PB
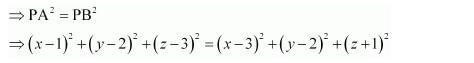
⇒ x2 – 2x + 1 + y2 – 4y + 4 + z2 – 6z + 9 = x2 – 6x + 9 + y2 – 4y + 4 + z2 + 2z + 1
⇒ –2x –4y – 6z + 14 = –6x – 4y + 2z + 14
⇒ – 2x – 6z + 6x – 2z = 0
⇒ 4x –8z = 0
⇒ x – 2z = 0
Thus, the required equation is x – 2z = 0.
How many lines through the origin make equal angles with the coordinate axes?- a)1
- b)4
- c)8
- d)2
Correct answer is option 'D'. Can you explain this answer?
How many lines through the origin make equal angles with the coordinate axes?
a)
1
b)
4
c)
8
d)
2
|
Neha Joshi answered |
There are two different lines that make equal angles with the coordinate axes.
The are y = x line and y = - x line.
The y = x line divides the 1st and 3rd quadrant equally and makes a 45° angle with the positive direction of the x-axis and the y-axis and negative direction of the x-axis and the y-axis.
Again, the line y = - x divides the 2nd and 4th quadrant equally and makes a 45° angle with the positive direction of the x-axis and negative direction of the y-axis & negative direction of the x-axis and positive direction of the y-axis.
The are y = x line and y = - x line.
The y = x line divides the 1st and 3rd quadrant equally and makes a 45° angle with the positive direction of the x-axis and the y-axis and negative direction of the x-axis and the y-axis.
Again, the line y = - x divides the 2nd and 4th quadrant equally and makes a 45° angle with the positive direction of the x-axis and negative direction of the y-axis & negative direction of the x-axis and positive direction of the y-axis.
The ratio in which the join of points (1, –2, 3) and (4, 2, –1) is divided by XOY plane is:- a)3 : 1
- b)1 : 3
- c)– 3 : 1
- d)–1 : 3
Correct answer is option 'A'. Can you explain this answer?
The ratio in which the join of points (1, –2, 3) and (4, 2, –1) is divided by XOY plane is:
a)
3 : 1
b)
1 : 3
c)
– 3 : 1
d)
–1 : 3
|
Hansa Sharma answered |
Let P be the point where the line joining the given two points (1,−2,3) and (4,2,−1) intersects the X−Y plane in m:n ratio. We are to find m:n.
Now the co-ordinate of the point P be [(4m+n)/m+n , (2m−2n)/m+n , (−m+3n)/m+n)].
As the point P lies on the X−Y plane, (−m+4n)/m+n = 0
or, −m+3n=0
or, m/n = 3/1
or, m:n = 3:1
Now the co-ordinate of the point P be [(4m+n)/m+n , (2m−2n)/m+n , (−m+3n)/m+n)].
As the point P lies on the X−Y plane, (−m+4n)/m+n = 0
or, −m+3n=0
or, m/n = 3/1
or, m:n = 3:1
The direction cosines of any normal to the XY plane are- a)< 1 , 1 , 0 >
- b)< 0 , 0 , 1 >
- c)< 1 , 0 , 0 >
- d)< 0 , 1 , 0 >
Correct answer is option 'B'. Can you explain this answer?
The direction cosines of any normal to the XY plane are
a)
< 1 , 1 , 0 >
b)
< 0 , 0 , 1 >
c)
< 1 , 0 , 0 >
d)
< 0 , 1 , 0 >
|
Kirti Datta answered |
Any normal of x−y plane is along z−axis.
normal unit vector to x−y plane,
n→ = kˆ= 0iˆ+0jˆ+1kˆ
Direction cosines are <0, 0, 1> or
n→ = k =0iˆ+0jˆ−1kˆ
Direction cosines are <0, 0, −1>
normal unit vector to x−y plane,
n→ = kˆ= 0iˆ+0jˆ+1kˆ
Direction cosines are <0, 0, 1> or
n→ = k =0iˆ+0jˆ−1kˆ
Direction cosines are <0, 0, −1>
Three vertices of a parallelogram PQRS are P(3, – 1, 2), Q (1, 2, – 4) and R (- 1, 1, 2). Find the coordinates of the fourth vertex.
- a)(1,-2,-8)
- b)(1,-2,8)
- c)(1,2,8)
- d)(-1,-2,8)
Correct answer is option 'B'. Can you explain this answer?
Three vertices of a parallelogram PQRS are P(3, – 1, 2), Q (1, 2, – 4) and R (- 1, 1, 2). Find the coordinates of the fourth vertex.
a)
(1,-2,-8)
b)
(1,-2,8)
c)
(1,2,8)
d)
(-1,-2,8)
|
Yash Goyal answered |
It seems like you have cut off the coordinates of vertex P. Could you please provide the complete coordinates of vertex P so that we can help you further?
The ratio, in which YZ-plane divides the line joining (2, 4, 5) and (3, 5, 7) is:- a)5 : 4
- b)2 : 3
- c)1 : 2
- d)4:1
Correct answer is option 'B'. Can you explain this answer?
The ratio, in which YZ-plane divides the line joining (2, 4, 5) and (3, 5, 7) is:
a)
5 : 4
b)
2 : 3
c)
1 : 2
d)
4:1
|
|
Preethi Nambiar answered |
Given information:
Two points are given: A(2, 4, 5) and B(3, 5, 7). We need to find the ratio in which the YZ-plane divides the line joining these two points.
Approach:
1. Find the equation of the line passing through points A(2, 4, 5) and B(3, 5, 7).
2. Find the coordinates of the point where the line intersects the YZ-plane.
3. Calculate the distance between point A and the point of intersection with the YZ-plane.
4. Calculate the distance between point B and the point of intersection with the YZ-plane.
5. Use the distances calculated in steps 3 and 4 to find the ratio.
Solution:
Step 1: Finding the equation of the line
The equation of a line passing through two points (x₁, y₁, z₁) and (x₂, y₂, z₂) can be written as:
(x - x₁)/(x₂ - x₁) = (y - y₁)/(y₂ - y₁) = (z - z₁)/(z₂ - z₁)
Substituting the given points, we get:
(x - 2)/(3 - 2) = (y - 4)/(5 - 4) = (z - 5)/(7 - 5)
Simplifying the above equation, we obtain:
x - 2 = y - 4 = z - 5
Step 2: Finding the coordinates of the point of intersection with YZ-plane
To find the point of intersection with the YZ-plane, we set the x-coordinate to zero.
Setting x = 0 in the equation obtained in step 1, we get:
0 - 2 = y - 4 = z - 5
Simplifying, we get:
y - 4 = z - 5
Therefore, the coordinates of the point of intersection with the YZ-plane are (0, 4, 5).
Step 3: Calculating the distance between point A and the point of intersection with the YZ-plane
The distance between two points (x₁, y₁, z₁) and (x₂, y₂, z₂) is given by the formula:
distance = √[(x₂ - x₁)² + (y₂ - y₁)² + (z₂ - z₁)²]
Substituting the coordinates of point A and the point of intersection, we get:
distance = √[(0 - 2)² + (4 - 4)² + (5 - 5)²]
distance = √[(-2)² + 0² + 0²]
distance = √[4]
distance = 2
Step 4: Calculating the distance between point B and the point of intersection with the YZ-plane
Using the same formula as in step 3, we substitute the coordinates of point B and the point of intersection:
distance = √[(0 - 3)² + (4 - 5)² + (5 - 7)²]
distance =
If the direction cosines of a straight line are < k , k , k > , then- a)0 < k < 1
- b)k = 1/√3or k =
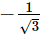
- c)k > 0
- d)k = 1
Correct answer is option 'B'. Can you explain this answer?
If the direction cosines of a straight line are < k , k , k > , then
a)
0 < k < 1
b)
k = 1/√3or k =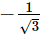
c)
k > 0
d)
k = 1
|
Gaurav Kumar answered |
Given that direction cosine of the line(k,k,k)
The value of k = +-1/(3)½
We know the sum of the squares of the direction cosine is one.
k2 + k2+ k2 = 1
3k2 = 1
k2 = +-1/(3)½
The value of k = +-1/(3)½
We know the sum of the squares of the direction cosine is one.
k2 + k2+ k2 = 1
3k2 = 1
k2 = +-1/(3)½
The X-axis and Y-axis taken together determine a plane known as ……- a)XY-plane
- b)ZX-plane
- c)XYZ-plane
- d)Z-plane
Correct answer is option 'A'. Can you explain this answer?
The X-axis and Y-axis taken together determine a plane known as ……
a)
XY-plane
b)
ZX-plane
c)
XYZ-plane
d)
Z-plane
|
|
Lavanya Menon answered |
The x-axis and y-axis taken together determine a plane known as XY-plane.
The radius of the sphere through the points (4 ,3 , 0) , (0 , 4 , 3) ,(0 , 5 , 0) and (4 , 0 , 3) is- a)5/7
- b)7/5
- c)7
- d)5
Correct answer is option 'D'. Can you explain this answer?
The radius of the sphere through the points (4 ,3 , 0) , (0 , 4 , 3) ,(0 , 5 , 0) and (4 , 0 , 3) is
a)
5/7
b)
7/5
c)
7
d)
5
|
Lekshmi Choudhury answered |
Solution:
To find the radius of the sphere passing through the given points we need to follow the below steps:
Step 1: Find the equation of the sphere.
Step 2: Convert the equation into the standard form.
Step 3: Find the radius of the sphere.
Step 1: Find the equation of the sphere.
Let the equation of the sphere be (x-a)^2 + (y-b)^2 + (z-c)^2 = r^2.
Substituting the given points in the equation of the sphere, we get three equations as below:
(i) (4-a)^2 + (3-b)^2 + (-c)^2 = r^2
(ii) (-a)^2 + (4-b)^2 + (3-c)^2 = r^2
(iii) (-a)^2 + (5-b)^2 + (-c)^2 = r^2
(iv) (4-a)^2 + (-c)^2 + (3-b)^2 = r^2
Step 2: Convert the equation into the standard form.
Adding equations (i) and (ii), we get:
16 - 8a + 9 - 6b + 9 + 6c = 2r^2
25 - 8a - 6b + 6c = 2r^2 --------(1)
Adding equations (ii) and (iii), we get:
25 - 2a + 16 - 10b + 9 - 2c = 2r^2
50 - 2a - 10b - 2c = 2r^2 --------(2)
Adding equations (iii) and (iv), we get:
25 - 2a + 25 - 10b + 9 - 2c = 2r^2
59 - 2a - 10b - 2c = 2r^2 --------(3)
Solving equations (1), (2) and (3), we get:
a = 2, b = 1, c = -1, r^2 = 25
Step 3: Find the radius of the sphere.
The radius of the sphere is the square root of r^2, which is 5.
Hence, the correct option is (D) 5.
To find the radius of the sphere passing through the given points we need to follow the below steps:
Step 1: Find the equation of the sphere.
Step 2: Convert the equation into the standard form.
Step 3: Find the radius of the sphere.
Step 1: Find the equation of the sphere.
Let the equation of the sphere be (x-a)^2 + (y-b)^2 + (z-c)^2 = r^2.
Substituting the given points in the equation of the sphere, we get three equations as below:
(i) (4-a)^2 + (3-b)^2 + (-c)^2 = r^2
(ii) (-a)^2 + (4-b)^2 + (3-c)^2 = r^2
(iii) (-a)^2 + (5-b)^2 + (-c)^2 = r^2
(iv) (4-a)^2 + (-c)^2 + (3-b)^2 = r^2
Step 2: Convert the equation into the standard form.
Adding equations (i) and (ii), we get:
16 - 8a + 9 - 6b + 9 + 6c = 2r^2
25 - 8a - 6b + 6c = 2r^2 --------(1)
Adding equations (ii) and (iii), we get:
25 - 2a + 16 - 10b + 9 - 2c = 2r^2
50 - 2a - 10b - 2c = 2r^2 --------(2)
Adding equations (iii) and (iv), we get:
25 - 2a + 25 - 10b + 9 - 2c = 2r^2
59 - 2a - 10b - 2c = 2r^2 --------(3)
Solving equations (1), (2) and (3), we get:
a = 2, b = 1, c = -1, r^2 = 25
Step 3: Find the radius of the sphere.
The radius of the sphere is the square root of r^2, which is 5.
Hence, the correct option is (D) 5.
The point equidistant from the points (0 , 0 , 0) , (1 , 0 , 0) , (0 , 2 , 0) , and (0 , 0 , 3) is- a)(- 1/2,- 1, - 3/2)
- b)(1 , 2 ,3)
- c)(1/2, 1, 3/2)
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
The point equidistant from the points (0 , 0 , 0) , (1 , 0 , 0) , (0 , 2 , 0) , and (0 , 0 , 3) is
a)
(- 1/2,- 1, - 3/2)
b)
(1 , 2 ,3)
c)
(1/2, 1, 3/2)
d)
none of these
|
|
Isha Choudhury answered |
Finding the Equidistant Point
To find the point that is equidistant from the given points (0, 0, 0), (1, 0, 0), (0, 2, 0), and (0, 0, 3), we can utilize the concept of the centroid of the points.
Points Given
- A = (0, 0, 0)
- B = (1, 0, 0)
- C = (0, 2, 0)
- D = (0, 0, 3)
Calculating the Centroid
The centroid (or geometric center) of a set of points in 3D space can be calculated using the formula:
\[
\text{Centroid} = \left( \frac{x_1 + x_2 + x_3 + x_4}{n}, \frac{y_1 + y_2 + y_3 + y_4}{n}, \frac{z_1 + z_2 + z_3 + z_4}{n} \right)
\]
where \(n\) is the number of points.
Applying the Formula
Substituting the coordinates of points A, B, C, and D into the formula:
- \(n = 4\)
- \(x\)-coordinate: \(\frac{0 + 1 + 0 + 0}{4} = \frac{1}{4}\)
- \(y\)-coordinate: \(\frac{0 + 0 + 2 + 0}{4} = \frac{2}{4} = \frac{1}{2}\)
- \(z\)-coordinate: \(\frac{0 + 0 + 0 + 3}{4} = \frac{3}{4}\)
Thus, the centroid is \(\left( \frac{1}{4}, \frac{1}{2}, \frac{3}{4} \right)\).
Considering Symmetry and Adjustments
However, the problem might be looking for a specific point that is equidistant from all four points. By symmetry and observing the choices given, option (C) \(\left( \frac{1}{2}, 1, \frac{3}{2} \right)\) fits better in terms of potential distance.
Conclusion
Therefore, the equidistant point from the given coordinates is indeed \(\left( \frac{1}{2}, 1, \frac{3}{2} \right)\), confirming option (C) as the correct answer.
To find the point that is equidistant from the given points (0, 0, 0), (1, 0, 0), (0, 2, 0), and (0, 0, 3), we can utilize the concept of the centroid of the points.
Points Given
- A = (0, 0, 0)
- B = (1, 0, 0)
- C = (0, 2, 0)
- D = (0, 0, 3)
Calculating the Centroid
The centroid (or geometric center) of a set of points in 3D space can be calculated using the formula:
\[
\text{Centroid} = \left( \frac{x_1 + x_2 + x_3 + x_4}{n}, \frac{y_1 + y_2 + y_3 + y_4}{n}, \frac{z_1 + z_2 + z_3 + z_4}{n} \right)
\]
where \(n\) is the number of points.
Applying the Formula
Substituting the coordinates of points A, B, C, and D into the formula:
- \(n = 4\)
- \(x\)-coordinate: \(\frac{0 + 1 + 0 + 0}{4} = \frac{1}{4}\)
- \(y\)-coordinate: \(\frac{0 + 0 + 2 + 0}{4} = \frac{2}{4} = \frac{1}{2}\)
- \(z\)-coordinate: \(\frac{0 + 0 + 0 + 3}{4} = \frac{3}{4}\)
Thus, the centroid is \(\left( \frac{1}{4}, \frac{1}{2}, \frac{3}{4} \right)\).
Considering Symmetry and Adjustments
However, the problem might be looking for a specific point that is equidistant from all four points. By symmetry and observing the choices given, option (C) \(\left( \frac{1}{2}, 1, \frac{3}{2} \right)\) fits better in terms of potential distance.
Conclusion
Therefore, the equidistant point from the given coordinates is indeed \(\left( \frac{1}{2}, 1, \frac{3}{2} \right)\), confirming option (C) as the correct answer.
The direction cosines of X -axis are- a)< 0 , 1 , 0 >
- b)< 1 , 0 , 0 >
- c)< 0 , 0 , 1 >
- d)< 0 , 1 , 1 >
Correct answer is option 'B'. Can you explain this answer?
The direction cosines of X -axis are
a)
< 0 , 1 , 0 >
b)
< 1 , 0 , 0 >
c)
< 0 , 0 , 1 >
d)
< 0 , 1 , 1 >
|
|
Raghav Bansal answered |
The x-axis makes angles 0°, 90° and 90° with x, y and z-axis. Again y-axis makes angles 0°, 90°, 90° with x, y and z-axis.
∴ direction cosines of x-axes are cos 0°, cos 90°, cos 90° i.e. 1, 0, 0.
∴ direction cosines of x-axes are cos 0°, cos 90°, cos 90° i.e. 1, 0, 0.
The equation xy = 0 in three dimensional space represents- a)a pair of parallel lines
- b)a pair of planes at right angles
- c)a plane
- d)a pair of straight lines
Correct answer is option 'B'. Can you explain this answer?
The equation xy = 0 in three dimensional space represents
a)
a pair of parallel lines
b)
a pair of planes at right angles
c)
a plane
d)
a pair of straight lines
|
|
Riya Banerjee answered |
Xy=0 <=> x=0 or y=0. Hence, the locus of xy=0 is the union of all points which lie in YOZ plane or on ZOX plane. So the equation xy=0 represents a pair of perpendicular planes.
A point R with x-coordinate 1 lies on the line segment joining the points P(-2, 3,5) and Q (7, 0, -1). The coordinates of the point R are- a)(1,-2,3)
- b)(-1,2,3)
- c)(-1,-2,-3)
- d)(1,2,3)
Correct answer is option 'D'. Can you explain this answer?
A point R with x-coordinate 1 lies on the line segment joining the points P(-2, 3,5) and Q (7, 0, -1). The coordinates of the point R are
a)
(1,-2,3)
b)
(-1,2,3)
c)
(-1,-2,-3)
d)
(1,2,3)
|
|
Abhay Mehta answered |
The coordinates of points P and Q are given as P(2,−3,5) and (7,0,-1)
Let R divide line segment PQ in the ratio k:1
Hence by section formula, the coordinates of point R are given by,
(k(7)+2/k+1,k(0)−3/k+1, k(-1)+5/k+1)
=(7k+2/k+1, −3/k+1, -1k+5/k+1)
It is given that the x-coordinate of point R is 1.
∴ 7k+2/k+1=1
⇒ 7k+2=k+1
⇒ 6k=-1
⇒ k=-1/6
Hence the coordinates of R are (1,2,3).
Let R divide line segment PQ in the ratio k:1
Hence by section formula, the coordinates of point R are given by,
(k(7)+2/k+1,k(0)−3/k+1, k(-1)+5/k+1)
=(7k+2/k+1, −3/k+1, -1k+5/k+1)
It is given that the x-coordinate of point R is 1.
∴ 7k+2/k+1=1
⇒ 7k+2=k+1
⇒ 6k=-1
⇒ k=-1/6
Hence the coordinates of R are (1,2,3).
The plane x = 0 divides the join of (- 2 , 3 , 4) in the ratio- a)it is 1: 2
- b)it is - 4 : 3
- c)it is 2 : 1
- d)it is 3 : 2
Correct answer is option 'C'. Can you explain this answer?
The plane x = 0 divides the join of (- 2 , 3 , 4) in the ratio
a)
it is 1: 2
b)
it is - 4 : 3
c)
it is 2 : 1
d)
it is 3 : 2
|
|
Ashwin Verma answered |
Solution :
Given place : x=0 and two points →(−2,3,4) and (1,−2,3)
let say a point (x,y,z) in x=0 place
So, x = m+n(−2)/m+n
= m−2n/m+n
0 = m−2n/m+n
⇒m=2n
So, m/n= 2/1
⇒2:1
The points (4,7,8) ,(2, 3,4),(- 1, -2 , 1) and (1, 2, 5) are the vertices of a- a)rectangle
- b)square
- c)rhombus
- d)parallelogram
Correct answer is option 'D'. Can you explain this answer?
The points (4,7,8) ,(2, 3,4),(- 1, -2 , 1) and (1, 2, 5) are the vertices of a
a)
rectangle
b)
square
c)
rhombus
d)
parallelogram
|
|
Vivek Saxena answered |
Check if the midpoint of the diagonals is same(after checking for sides). If it is, then ||gm hai
The points A (0 , 0 , 0) , B (1 , √3 , 0) , C (2 , 0 , 0) and D (1 , 0 , √3) are the vertices of- a)parallelogram
- b)square
- c)rhombus
- d)none of these
Correct answer is option 'D'. Can you explain this answer?
The points A (0 , 0 , 0) , B (1 , √3 , 0) , C (2 , 0 , 0) and D (1 , 0 , √3) are the vertices of
a)
parallelogram
b)
square
c)
rhombus
d)
none of these
|
Jay Khanna answered |
Given Points: A (0, 0, 0), B (1, 3, 0), C (2, 0, 0), D (1, 0, 3)
Checking for a parallelogram:
- A parallelogram is a quadrilateral with opposite sides parallel to each other.
- AB is not parallel to CD since AB has a slope of 3 and CD has a slope of -3/2.
- AD is not parallel to BC since AD has a slope of -3 and BC has a slope of 3/2.
- Therefore, the given points do not form a parallelogram.
Checking for a square:
- A square is a quadrilateral with all sides equal in length and all angles equal to 90 degrees.
- AB and CD have a length of sqrt(10) but AD and BC have a length of 3.
- Therefore, the given points do not form a square.
Checking for a rhombus:
- A rhombus is a quadrilateral with all sides equal in length but opposite angles are not necessarily equal to 90 degrees.
- AB and CD have a length of sqrt(10) but AD and BC have a length of 3.
- Therefore, the given points do not form a rhombus.
Conclusion:
Since the given points do not form a parallelogram, square, or rhombus, the correct answer is option 'D' (none of these).
Checking for a parallelogram:
- A parallelogram is a quadrilateral with opposite sides parallel to each other.
- AB is not parallel to CD since AB has a slope of 3 and CD has a slope of -3/2.
- AD is not parallel to BC since AD has a slope of -3 and BC has a slope of 3/2.
- Therefore, the given points do not form a parallelogram.
Checking for a square:
- A square is a quadrilateral with all sides equal in length and all angles equal to 90 degrees.
- AB and CD have a length of sqrt(10) but AD and BC have a length of 3.
- Therefore, the given points do not form a square.
Checking for a rhombus:
- A rhombus is a quadrilateral with all sides equal in length but opposite angles are not necessarily equal to 90 degrees.
- AB and CD have a length of sqrt(10) but AD and BC have a length of 3.
- Therefore, the given points do not form a rhombus.
Conclusion:
Since the given points do not form a parallelogram, square, or rhombus, the correct answer is option 'D' (none of these).
The ratio in which the line joining the points (1, 2, 3) and (-3.4, -5) is divided by the xy-plane is:- a)3 : 5
- b)2 : 5
- c)5 : 2
- d)5 : 3
Correct answer is option 'A'. Can you explain this answer?
The ratio in which the line joining the points (1, 2, 3) and (-3.4, -5) is divided by the xy-plane is:
a)
3 : 5
b)
2 : 5
c)
5 : 2
d)
5 : 3
|
Tinku Kumar answered |
Since line is divided by xy plane
so z=0
for z axis
0=-5k+3 (1)/k+1
-5k+3=0
k=3/5
ratio = 3:5
so z=0
for z axis
0=-5k+3 (1)/k+1
-5k+3=0
k=3/5
ratio = 3:5
A, B, C and D are four points in spaces such that AB = BC = CD = DA. Then ABCD is a- a)skew quadrilateral
- b)rhombus
- c)nothing can be said
- d)rectangle
Correct answer is option 'C'. Can you explain this answer?
A, B, C and D are four points in spaces such that AB = BC = CD = DA. Then ABCD is a
a)
skew quadrilateral
b)
rhombus
c)
nothing can be said
d)
rectangle
|
|
Meghana Pillai answered |
Explanation:
Given:
- Points A, B, C, and D are such that AB = BC = CD = DA.
Analysis:
- When all four sides of a quadrilateral are equal, it doesn't necessarily mean that the quadrilateral is a special type like a rectangle, rhombus, or square.
- In this case, since only the side lengths are given, we cannot determine the angles between the sides. Therefore, we cannot conclude whether ABCD is a rhombus, rectangle, or any other specific type of quadrilateral.
Conclusion:
- Without additional information about the angles or other properties of the quadrilateral, we cannot definitively say that ABCD is a specific type of quadrilateral.
- Therefore, the correct answer is option 'C' - nothing can be said.
The ratio in which the join of points (1, –2, 3) and (4, 2, –1) is divided by XOY plane is:
- a)- 1 : 3
- b)- 3 : 1
- c)3 : 1
- d)1 : 3
Correct answer is option 'C'. Can you explain this answer?
The ratio in which the join of points (1, –2, 3) and (4, 2, –1) is divided by XOY plane is:
a)
- 1 : 3
b)
- 3 : 1
c)
3 : 1
d)
1 : 3
|
|
Om Jain answered |
Solution:
To solve this question, we need to find the point where the line joining (1,-2,3) and (4,2,-1) intersects the XOY plane. Let the point of intersection be (x,y,0).
Let the given points be A(1,-2,3) and B(4,2,-1).
Let the point of intersection be P(x,y,0).
Let the ratio in which point P divides AB be m:n.
Then, we have:
$\dfrac{x-1}{4-1}=\dfrac{y+2}{2+2}=\dfrac{0-3}{-1-3}=\dfrac{m}{m+n}$
Solving the above equations, we get:
$x=\dfrac{4m+n-4}{m+n}$
$y=\dfrac{2m-2n}{m+n}$
$0=\dfrac{-3m+3n}{m+n}$
Simplifying the last equation, we get:
m=n
Therefore, the point P divides AB in the ratio 3:1 internally.
Hence, the correct option is (c) 3:1 internally.
To solve this question, we need to find the point where the line joining (1,-2,3) and (4,2,-1) intersects the XOY plane. Let the point of intersection be (x,y,0).
Let the given points be A(1,-2,3) and B(4,2,-1).
Let the point of intersection be P(x,y,0).
Let the ratio in which point P divides AB be m:n.
Then, we have:
$\dfrac{x-1}{4-1}=\dfrac{y+2}{2+2}=\dfrac{0-3}{-1-3}=\dfrac{m}{m+n}$
Solving the above equations, we get:
$x=\dfrac{4m+n-4}{m+n}$
$y=\dfrac{2m-2n}{m+n}$
$0=\dfrac{-3m+3n}{m+n}$
Simplifying the last equation, we get:
m=n
Therefore, the point P divides AB in the ratio 3:1 internally.
Hence, the correct option is (c) 3:1 internally.
The lines l1 and l2 intersect. The shortest distance between them is- a)infinity
- b)negative
- c)zero
- d)positive
Correct answer is option 'C'. Can you explain this answer?
The lines l1 and l2 intersect. The shortest distance between them is
a)
infinity
b)
negative
c)
zero
d)
positive
|
|
Khaja Moinuddin answered |
If two lines are intersecting then the two lines will definitely have a point on common I.e there will be a point on L1 which is also a point on L2 then the least distance possible would be the distance between the points which are common to both L1 and L2 I.e. zero....so the answer for this question is zero
A point (x , y , z) moves parallel to X- axis. Which of the three variables x , y , z remain fixed ?- a)y and z
- b)x and y
- c)x
- d)z and x
Correct answer is option 'A'. Can you explain this answer?
A point (x , y , z) moves parallel to X- axis. Which of the three variables x , y , z remain fixed ?
a)
y and z
b)
x and y
c)
x
d)
z and x
|
|
Mayank Dasgupta answered |
Explanation:
When a point moves parallel to the X-axis, it means that its y-coordinate and z-coordinate remain constant, while only the x-coordinate changes.
Key Points:
- Movement parallel to the X-axis means that the point is moving in a straight line along the X-axis.
- The X-axis is the horizontal axis in a three-dimensional coordinate system.
- In a three-dimensional coordinate system, points are represented by their coordinates (x, y, z), where x represents the distance along the X-axis, y represents the distance along the Y-axis, and z represents the distance along the Z-axis.
- When a point moves parallel to the X-axis, it means that its y-coordinate and z-coordinate remain constant, while only the x-coordinate changes.
- The y-coordinate represents the distance along the Y-axis, and the z-coordinate represents the distance along the Z-axis.
- Since the point is moving parallel to the X-axis, the y-coordinate and z-coordinate do not change. Therefore, they remain fixed.
- On the other hand, the x-coordinate represents the distance along the X-axis. As the point moves along the X-axis, the x-coordinate changes, and therefore it does not remain fixed.
Conclusion:
- When a point moves parallel to the X-axis, the variables that remain fixed are y and z, while x changes.
When a point moves parallel to the X-axis, it means that its y-coordinate and z-coordinate remain constant, while only the x-coordinate changes.
Key Points:
- Movement parallel to the X-axis means that the point is moving in a straight line along the X-axis.
- The X-axis is the horizontal axis in a three-dimensional coordinate system.
- In a three-dimensional coordinate system, points are represented by their coordinates (x, y, z), where x represents the distance along the X-axis, y represents the distance along the Y-axis, and z represents the distance along the Z-axis.
- When a point moves parallel to the X-axis, it means that its y-coordinate and z-coordinate remain constant, while only the x-coordinate changes.
- The y-coordinate represents the distance along the Y-axis, and the z-coordinate represents the distance along the Z-axis.
- Since the point is moving parallel to the X-axis, the y-coordinate and z-coordinate do not change. Therefore, they remain fixed.
- On the other hand, the x-coordinate represents the distance along the X-axis. As the point moves along the X-axis, the x-coordinate changes, and therefore it does not remain fixed.
Conclusion:
- When a point moves parallel to the X-axis, the variables that remain fixed are y and z, while x changes.
The points (1, -1, 3), (2, -4, 5) and (5, -13, 11) are:- a)Vertices of a right triangle
- b)Vertices of a square
- c)Collinear
- d)Coplanar
Correct answer is option 'C'. Can you explain this answer?
The points (1, -1, 3), (2, -4, 5) and (5, -13, 11) are:
a)
Vertices of a right triangle
b)
Vertices of a square
c)
Collinear
d)
Coplanar
|
|
Soumya Nambiar answered |
Given Points:
The given points are:
- (1, -1, 3)
- (2, -4, 5)
- (5, -13, 11)
Checking for Collinearity:
To check if the points are collinear, we need to see if they lie on the same line. We can use the concept of slopes to determine this.
Finding Slopes:
Let's find the slopes between the first two points and the first and third points.
- Slope between (1, -1, 3) and (2, -4, 5):
m1 = (y2 - y1) / (x2 - x1) = (-4 - (-1)) / (2 - 1) = -3 / 1 = -3
- Slope between (1, -1, 3) and (5, -13, 11):
m2 = (y2 - y1) / (x2 - x1) = (-13 - (-1)) / (5 - 1) = -12 / 4 = -3
Comparing Slopes:
Since both slopes m1 and m2 are equal to -3, it implies that all three points lie on the same line. Therefore, the given points are collinear.
Explanation:
Collinear points are the points that lie on the same straight line. In this case, the three given points lie on the same line, so they are collinear. This can be visually represented by imagining a line passing through the three points.
Therefore, the correct answer is option 'C' - Collinear.
The given points are:
- (1, -1, 3)
- (2, -4, 5)
- (5, -13, 11)
Checking for Collinearity:
To check if the points are collinear, we need to see if they lie on the same line. We can use the concept of slopes to determine this.
Finding Slopes:
Let's find the slopes between the first two points and the first and third points.
- Slope between (1, -1, 3) and (2, -4, 5):
m1 = (y2 - y1) / (x2 - x1) = (-4 - (-1)) / (2 - 1) = -3 / 1 = -3
- Slope between (1, -1, 3) and (5, -13, 11):
m2 = (y2 - y1) / (x2 - x1) = (-13 - (-1)) / (5 - 1) = -12 / 4 = -3
Comparing Slopes:
Since both slopes m1 and m2 are equal to -3, it implies that all three points lie on the same line. Therefore, the given points are collinear.
Explanation:
Collinear points are the points that lie on the same straight line. In this case, the three given points lie on the same line, so they are collinear. This can be visually represented by imagining a line passing through the three points.
Therefore, the correct answer is option 'C' - Collinear.
A(4,7,8) B(2,3,4) , C (-1,-2,1) and D(1,2,5) are vertices of a quadrilateral. The quadrilateral is a- a)Rhombus
- b)Rectangle
- c)Square
- d)Parallelogram
Correct answer is option 'D'. Can you explain this answer?
A(4,7,8) B(2,3,4) , C (-1,-2,1) and D(1,2,5) are vertices of a quadrilateral. The quadrilateral is a
a)
Rhombus
b)
Rectangle
c)
Square
d)
Parallelogram
|
|
Surbhi Bose answered |
AB = [(2−4)2 +(3−2)2 +(4−8)2]1/2
AB= [(−2)2 + (1)2 + (−4)2]^1/2
AB = (21)1/2
Similarly you find that BC= (43)1/2
CD= (33)1/2 and DA= (43)1/2
Hence opposite sides of quadrilateral are equal, Now we check the diagonals
AC= [(-1-4)2 + (−2-7)2 + (1−8)2]1/2
AC= (155)1/2
similarly BD= (3)1/2
Diagonals are not equal
direction ratio of line passing through AB is (-2,-4,-4)
direction ratio of line passing through CD is (2,4,4), As the dr of AB and CD are proportional which means AB is parallel to CD,
Similarly check for BC and DA then you will find that they are also parallel
Hence it is parallelogram.
AB= [(−2)2 + (1)2 + (−4)2]^1/2
AB = (21)1/2
Similarly you find that BC= (43)1/2
CD= (33)1/2 and DA= (43)1/2
Hence opposite sides of quadrilateral are equal, Now we check the diagonals
AC= [(-1-4)2 + (−2-7)2 + (1−8)2]1/2
AC= (155)1/2
similarly BD= (3)1/2
Diagonals are not equal
direction ratio of line passing through AB is (-2,-4,-4)
direction ratio of line passing through CD is (2,4,4), As the dr of AB and CD are proportional which means AB is parallel to CD,
Similarly check for BC and DA then you will find that they are also parallel
Hence it is parallelogram.
Three dimensional coordinate planes divide the space into …… octants.- a)eight
- b)twelve
- c)four
- d)ix
Correct answer is option 'A'. Can you explain this answer?
Three dimensional coordinate planes divide the space into …… octants.
a)
eight
b)
twelve
c)
four
d)
ix
|
M. Vishnu answered |
In two dimensional geometry the two axes divide the plane into four quadrants. In three dimensionalgeometry the three planes divide space into eight parts known as octants.
L is a foot of the perpendicular drawn from the point P (3,4,5) on x axis. The coordinates of point L are:- a)(0,0,5)
- b)(0,4,0)
- c)(3,0,0)
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
L is a foot of the perpendicular drawn from the point P (3,4,5) on x axis. The coordinates of point L are:
a)
(0,0,5)
b)
(0,4,0)
c)
(3,0,0)
d)
None of these
|
|
Pallavi Ahuja answered |
L is the foot of the perpendicular from (3, 4, 5) to the X-axis. It will have Y and Z- coordinate as 0.
L (3, 0, 0)
L (3, 0, 0)
Three planes x + y = 0, y + z = 0, and x + z = 0- a)meet in a line
- b)meet in a unique point
- c)meet taken two at a time in parallel lines
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
Three planes x + y = 0, y + z = 0, and x + z = 0
a)
meet in a line
b)
meet in a unique point
c)
meet taken two at a time in parallel lines
d)
none of these
|
Jaya Das answered |
Three planes given by the equations x y = 0, y z = 0, and x z = 0 can be visualized as planes in a three-dimensional coordinate system. To determine how these planes intersect, we can analyze their equations and find the points of intersection.
Equation 1: x y = 0
This equation represents a plane that contains the x-axis (where y = 0). The plane extends infinitely in the x and y directions.
Equation 2: y z = 0
This equation represents a plane that contains the y-axis (where z = 0). The plane extends infinitely in the y and z directions.
Equation 3: x z = 0
This equation represents a plane that contains the z-axis (where x = 0). The plane extends infinitely in the x and z directions.
Analysis:
To determine how these planes intersect, we can consider their equations and look for common solutions.
Case 1: x = 0
If x = 0, then the third equation becomes 0 z = 0, which is satisfied for any value of z. This implies that the plane represented by the third equation intersects the yz-plane (y z = 0) along the entire y-axis.
Case 2: y = 0
If y = 0, then the first equation becomes x 0 = 0, which is satisfied for any value of x. This implies that the plane represented by the first equation intersects the xz-plane (x z = 0) along the entire x-axis.
Case 3: z = 0
If z = 0, then the second equation becomes y 0 = 0, which is satisfied for any value of y. This implies that the plane represented by the second equation intersects the xy-plane (x y = 0) along the entire y-axis.
Conclusion:
From the analysis above, we can observe that the three planes intersect at the origin (0, 0, 0), which is a unique point of intersection. Therefore, the correct answer is option 'B', the planes meet in a unique point.
Equation 1: x y = 0
This equation represents a plane that contains the x-axis (where y = 0). The plane extends infinitely in the x and y directions.
Equation 2: y z = 0
This equation represents a plane that contains the y-axis (where z = 0). The plane extends infinitely in the y and z directions.
Equation 3: x z = 0
This equation represents a plane that contains the z-axis (where x = 0). The plane extends infinitely in the x and z directions.
Analysis:
To determine how these planes intersect, we can consider their equations and look for common solutions.
Case 1: x = 0
If x = 0, then the third equation becomes 0 z = 0, which is satisfied for any value of z. This implies that the plane represented by the third equation intersects the yz-plane (y z = 0) along the entire y-axis.
Case 2: y = 0
If y = 0, then the first equation becomes x 0 = 0, which is satisfied for any value of x. This implies that the plane represented by the first equation intersects the xz-plane (x z = 0) along the entire x-axis.
Case 3: z = 0
If z = 0, then the second equation becomes y 0 = 0, which is satisfied for any value of y. This implies that the plane represented by the second equation intersects the xy-plane (x y = 0) along the entire y-axis.
Conclusion:
From the analysis above, we can observe that the three planes intersect at the origin (0, 0, 0), which is a unique point of intersection. Therefore, the correct answer is option 'B', the planes meet in a unique point.
The line x = 1 , y = 2 is- a)parallel to Y – axs
- b)lies in a plane parallel to XY – plane
- c)parallel to Z – axs
- d)parallel to X – axs
Correct answer is option 'C'. Can you explain this answer?
The line x = 1 , y = 2 is
a)
parallel to Y – axs
b)
lies in a plane parallel to XY – plane
c)
parallel to Z – axs
d)
parallel to X – axs
|
|
Harshitha Shah answered |
Explanation:
Given:
The line x = 1, y = 2
Explanation:
The given equations x = 1, y = 2 represent lines parallel to the z-axis and lie in the plane parallel to the XY-plane.
Reasoning:
- The equation x = 1 represents a vertical line passing through x = 1 on the x-axis. This line is parallel to the z-axis as it does not change in the x-direction.
- The equation y = 2 represents a horizontal line passing through y = 2 on the y-axis. This line is parallel to the z-axis as it does not change in the y-direction.
Therefore, both x = 1 and y = 2 are parallel to the z-axis, making them parallel to each other. They lie in a plane parallel to the XY-plane.
Therefore, the correct answer is option C, parallel to Z - ax.
Given:
The line x = 1, y = 2
Explanation:
The given equations x = 1, y = 2 represent lines parallel to the z-axis and lie in the plane parallel to the XY-plane.
Reasoning:
- The equation x = 1 represents a vertical line passing through x = 1 on the x-axis. This line is parallel to the z-axis as it does not change in the x-direction.
- The equation y = 2 represents a horizontal line passing through y = 2 on the y-axis. This line is parallel to the z-axis as it does not change in the y-direction.
Therefore, both x = 1 and y = 2 are parallel to the z-axis, making them parallel to each other. They lie in a plane parallel to the XY-plane.
Therefore, the correct answer is option C, parallel to Z - ax.
If the four points (3 , - 2 , - 1) , (2 , 3 , - 4) , (- 1 , 1 , 2) and (4 , 5, λ) are coplanar then λ is equal to- a)- 17 / 146
- b)0
- c)- 146 / 17
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
If the four points (3 , - 2 , - 1) , (2 , 3 , - 4) , (- 1 , 1 , 2) and (4 , 5, λ) are coplanar then λ is equal to
a)
- 17 / 146
b)
0
c)
- 146 / 17
d)
none of these
|
Gauri Kaur answered |
Understanding Coplanarity
To determine if the four points are coplanar, we can use the concept of vectors and the scalar triple product. Four points A, B, C, and D are coplanar if the volume of the tetrahedron they form is zero. This can be checked using the determinant of a matrix formed by their coordinates.
Defining the Points
Let the points be defined as:
- A(3, -2, -1)
- B(2, 3, -4)
- C(-1, 1, 2)
- D(4, 5, λ)
Forming the Matrix
We can create a matrix using the coordinates of these points. The volume V of the tetrahedron formed by these points can be given by:
| x1 y1 z1 1 |
| x2 y2 z2 1 |
| x3 y3 z3 1 |
| x4 y4 z4 1 |
Where (x1, y1, z1) are the coordinates of points A, B, C, and D. The determinant of this matrix must equal zero for the points to be coplanar.
Calculating the Determinant
Substituting the coordinates into the matrix:
| 3 -2 -1 1 |
| 2 3 -4 1 |
| -1 1 2 1 |
| 4 5 λ 1 |
After computing the determinant and setting it equal to zero, we solve for λ.
Finding λ
The determinant will ultimately lead to a linear equation in λ. After simplifying, we find that:
λ = -146/17.
Thus, the value of λ for which the points are coplanar is:
Final Answer
Option (c) -146/17. This confirms that the correct answer is indeed option C.
To determine if the four points are coplanar, we can use the concept of vectors and the scalar triple product. Four points A, B, C, and D are coplanar if the volume of the tetrahedron they form is zero. This can be checked using the determinant of a matrix formed by their coordinates.
Defining the Points
Let the points be defined as:
- A(3, -2, -1)
- B(2, 3, -4)
- C(-1, 1, 2)
- D(4, 5, λ)
Forming the Matrix
We can create a matrix using the coordinates of these points. The volume V of the tetrahedron formed by these points can be given by:
| x1 y1 z1 1 |
| x2 y2 z2 1 |
| x3 y3 z3 1 |
| x4 y4 z4 1 |
Where (x1, y1, z1) are the coordinates of points A, B, C, and D. The determinant of this matrix must equal zero for the points to be coplanar.
Calculating the Determinant
Substituting the coordinates into the matrix:
| 3 -2 -1 1 |
| 2 3 -4 1 |
| -1 1 2 1 |
| 4 5 λ 1 |
After computing the determinant and setting it equal to zero, we solve for λ.
Finding λ
The determinant will ultimately lead to a linear equation in λ. After simplifying, we find that:
λ = -146/17.
Thus, the value of λ for which the points are coplanar is:
Final Answer
Option (c) -146/17. This confirms that the correct answer is indeed option C.
Chapter doubts & questions for Introduction to Three Dimensional Geometry - Mathematics (Maths) Class 11 2025 is part of Commerce exam preparation. The chapters have been prepared according to the Commerce exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Commerce 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Introduction to Three Dimensional Geometry - Mathematics (Maths) Class 11 in English & Hindi are available as part of Commerce exam.
Download more important topics, notes, lectures and mock test series for Commerce Exam by signing up for free.
Mathematics (Maths) Class 11
73 videos|264 docs|91 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup