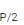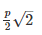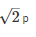All Exams >
Mechanical Engineering >
Mechanical Engineering SSC JE (Technical) >
All Questions
All questions of Engineering Mechanics for Mechanical Engineering Exam
A bucket of water weighing 10 kg is pulled up from a 20 m deep well by a rope weighing 1 kg/m length, then the work done is _____.- a)200 kg-m
- b)400 kg-m
- c)500 kg-m
- d)600 kg-m
Correct answer is option 'B'. Can you explain this answer?
A bucket of water weighing 10 kg is pulled up from a 20 m deep well by a rope weighing 1 kg/m length, then the work done is _____.
a)
200 kg-m
b)
400 kg-m
c)
500 kg-m
d)
600 kg-m
|
Mahi Kaur answered |
Let at a distance of x, weight to be pulled is 10 kg of bucket and x kg of rope weight.
So total weight is (10+x)
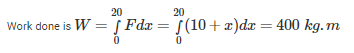
The position of a particle in rectilinear motion is given by the equation (x = t3 - 2t2 + 10t - 4), where x is in meters and t is in seconds. What will be the velocity of the particle at 3s?- a)20 m/s
- b)25 m/s
- c)15 m/s
- d)30 m/s
Correct answer is option 'B'. Can you explain this answer?
The position of a particle in rectilinear motion is given by the equation (x = t3 - 2t2 + 10t - 4), where x is in meters and t is in seconds. What will be the velocity of the particle at 3s?
a)
20 m/s
b)
25 m/s
c)
15 m/s
d)
30 m/s
|
Sinjini Bose answered |
Position (x) = t3 – 2t2 + 10t – 4
Velocity (v) =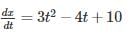 
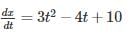
At t = 3 s
V = 3 × 32 – 4 × 3 + 10 = 25 m/s
The Force applied on a body of mass 100 kg to produce an acceleration of 5 m/s2, is- a)20 N
- b)100 N
- c)500 N
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
The Force applied on a body of mass 100 kg to produce an acceleration of 5 m/s2, is
a)
20 N
b)
100 N
c)
500 N
d)
None of these
|
Nandini Basak answered |
Acccording to Newton's Second Law of Motion:
F=ma=100×5=500kg−m/s2
A beam is fixed at one end and is vertically supported at the other end. What is the degree of statical indeterminacy?- a)1
- b)2
- c)3
- d)4
Correct answer is option 'A'. Can you explain this answer?
A beam is fixed at one end and is vertically supported at the other end. What is the degree of statical indeterminacy?
a)
1
b)
2
c)
3
d)
4
|
Sagarika Mukherjee answered |
If the number of independent static equilibrium equations is not sufficient for solving all the external and internal forces in a system, then the system is said to be statically indeterminate.
Degree of static indeterminacy = Total no. of unknowns (External and internal) – Number of independent equations of equilibrium.
Now in this problem,
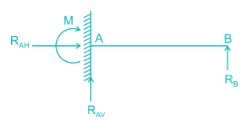
No. of unknowns = 4 (RAH, RAV, M and RB)
No. of independent equations of equilibrium = 3 (∑H = 0, ∑V = 0, ∑M = 0)
∴ Degree of static indeterminacy - 4 - 3 = 1
A 13 m ladder is placed against a smooth vertical wall with its lower end 5 m from the wall. What should be the coefficient of friction between the ladder and floor so that it remains in equilibrium?- a)0.1
- b)0.15
- c)0.28
- d)None of these
Correct answer is option 'D'. Can you explain this answer?
A 13 m ladder is placed against a smooth vertical wall with its lower end 5 m from the wall. What should be the coefficient of friction between the ladder and floor so that it remains in equilibrium?
a)
0.1
b)
0.15
c)
0.28
d)
None of these
|
|
Aman Ghosh answered |
Without knowing the weight of the ladder, coefficient of friction between the ladder and floor cannot be found.
A circular disc rolls down an inclined plane, the fraction of its total energy associated with its rotation is _____- a)1/2
- b)1/3
- c)1/4
- d)2/3
Correct answer is option 'B'. Can you explain this answer?
A circular disc rolls down an inclined plane, the fraction of its total energy associated with its rotation is _____
a)
1/2
b)
1/3
c)
1/4
d)
2/3
|
Rashi Chauhan answered |
Introduction:
When a circular disc rolls down an inclined plane, it possesses both translational and rotational energy. The fraction of its total energy associated with its rotation can be determined by understanding the concept of rotational kinetic energy.
Explanation:
1. Translational Kinetic Energy:
The translational kinetic energy of the rolling disc is given by the formula:
KE_translational = 1/2 * m * v^2
where m is the mass of the disc and v is its linear velocity.
2. Rotational Kinetic Energy:
The rotational kinetic energy of the rolling disc is given by the formula:
KE_rotational = 1/2 * I * ω^2
where I is the moment of inertia of the disc and ω is its angular velocity.
3. Relationship between Linear and Angular Velocity:
For a rolling disc, the linear velocity v of its center and the angular velocity ω of its rotation are related by the equation:
v = ω * R
where R is the radius of the disc.
4. Relationship between Moment of Inertia and Mass:
The moment of inertia I of a disc of uniform density can be calculated using the formula:
I = 1/2 * m * R^2
where m is the mass of the disc and R is its radius.
5. Total Energy of the Rolling Disc:
The total energy E of the rolling disc is the sum of its translational kinetic energy and rotational kinetic energy:
E = KE_translational + KE_rotational
Substituting the equations for translational and rotational kinetic energy, we get:
E = 1/2 * m * v^2 + 1/2 * I * ω^2
Using the relationships between linear and angular velocity (v = ω * R) and moment of inertia and mass (I = 1/2 * m * R^2), we can simplify the equation as:
E = 1/2 * m * v^2 + 1/2 * (1/2 * m * R^2) * (v/R)^2
Simplifying further, we get:
E = 1/2 * m * v^2 + 1/4 * m * v^2
E = 3/4 * m * v^2
6. Fraction of Energy Associated with Rotation:
To calculate the fraction of the total energy associated with rotation, we divide the rotational kinetic energy by the total energy:
Fraction of energy associated with rotation = KE_rotational / E
Plugging in the values, we have:
Fraction of energy associated with rotation = (1/2 * I * ω^2) / (3/4 * m * v^2)
Simplifying, we get:
Fraction of energy associated with rotation = 2/3
Therefore, the correct answer is option B) 1/3.
When a circular disc rolls down an inclined plane, it possesses both translational and rotational energy. The fraction of its total energy associated with its rotation can be determined by understanding the concept of rotational kinetic energy.
Explanation:
1. Translational Kinetic Energy:
The translational kinetic energy of the rolling disc is given by the formula:
KE_translational = 1/2 * m * v^2
where m is the mass of the disc and v is its linear velocity.
2. Rotational Kinetic Energy:
The rotational kinetic energy of the rolling disc is given by the formula:
KE_rotational = 1/2 * I * ω^2
where I is the moment of inertia of the disc and ω is its angular velocity.
3. Relationship between Linear and Angular Velocity:
For a rolling disc, the linear velocity v of its center and the angular velocity ω of its rotation are related by the equation:
v = ω * R
where R is the radius of the disc.
4. Relationship between Moment of Inertia and Mass:
The moment of inertia I of a disc of uniform density can be calculated using the formula:
I = 1/2 * m * R^2
where m is the mass of the disc and R is its radius.
5. Total Energy of the Rolling Disc:
The total energy E of the rolling disc is the sum of its translational kinetic energy and rotational kinetic energy:
E = KE_translational + KE_rotational
Substituting the equations for translational and rotational kinetic energy, we get:
E = 1/2 * m * v^2 + 1/2 * I * ω^2
Using the relationships between linear and angular velocity (v = ω * R) and moment of inertia and mass (I = 1/2 * m * R^2), we can simplify the equation as:
E = 1/2 * m * v^2 + 1/2 * (1/2 * m * R^2) * (v/R)^2
Simplifying further, we get:
E = 1/2 * m * v^2 + 1/4 * m * v^2
E = 3/4 * m * v^2
6. Fraction of Energy Associated with Rotation:
To calculate the fraction of the total energy associated with rotation, we divide the rotational kinetic energy by the total energy:
Fraction of energy associated with rotation = KE_rotational / E
Plugging in the values, we have:
Fraction of energy associated with rotation = (1/2 * I * ω^2) / (3/4 * m * v^2)
Simplifying, we get:
Fraction of energy associated with rotation = 2/3
Therefore, the correct answer is option B) 1/3.
The moment of inertia of a square of side (a) about an axis though its center of gravity is - a)a4/4
- b)a4/8
- c)a4/12
- d)a4/36
Correct answer is option 'C'. Can you explain this answer?
The moment of inertia of a square of side (a) about an axis though its center of gravity is
a)
a4/4
b)
a4/8
c)
a4/12
d)
a4/36
|
|
Aman Ghosh answered |
Moment of inertia of a rectangle about an axis though its center of gravity is bd3/12 and of a square is a4/12.
The torque acting on a body, rotating with angular acceleration of ‘α’ is given by which of the following relation?- a)T = Iα
- b)T = Iα2
- c)T = I2 α
- d)T = I2 α2
Correct answer is option 'A'. Can you explain this answer?
The torque acting on a body, rotating with angular acceleration of ‘α’ is given by which of the following relation?
a)
T = Iα
b)
T = Iα2
c)
T = I2 α
d)
T = I2 α2
|
Jithin Choudhury answered |
Explanation:
Torque and Angular Acceleration:
- Torque is the rotational equivalent of force and is defined as the tendency of a force to rotate an object about an axis.
- Angular acceleration (α) is the rate of change of angular velocity with respect to time.
Relation between Torque and Angular Acceleration:
- The torque acting on a body rotating with angular acceleration is directly proportional to the moment of inertia (I) of the body and the angular acceleration (α) itself.
- Mathematically, the relation is represented as T = Iα, where T is the torque, I is the moment of inertia, and α is the angular acceleration.
Explanation of the Correct Answer:
- Option 'A' (T = Iα) is the correct relation between torque and angular acceleration.
- This relation signifies that the torque acting on a body is directly proportional to the product of the moment of inertia and the angular acceleration.
- It is important to understand this relation in order to analyze the rotational motion of objects and calculate the torques involved.
Therefore, the correct relation between torque and angular acceleration is T = Iα, as stated in option 'A'. Understanding this relation is essential in the field of mechanical engineering when dealing with rotational dynamics and motion.
Torque and Angular Acceleration:
- Torque is the rotational equivalent of force and is defined as the tendency of a force to rotate an object about an axis.
- Angular acceleration (α) is the rate of change of angular velocity with respect to time.
Relation between Torque and Angular Acceleration:
- The torque acting on a body rotating with angular acceleration is directly proportional to the moment of inertia (I) of the body and the angular acceleration (α) itself.
- Mathematically, the relation is represented as T = Iα, where T is the torque, I is the moment of inertia, and α is the angular acceleration.
Explanation of the Correct Answer:
- Option 'A' (T = Iα) is the correct relation between torque and angular acceleration.
- This relation signifies that the torque acting on a body is directly proportional to the product of the moment of inertia and the angular acceleration.
- It is important to understand this relation in order to analyze the rotational motion of objects and calculate the torques involved.
Therefore, the correct relation between torque and angular acceleration is T = Iα, as stated in option 'A'. Understanding this relation is essential in the field of mechanical engineering when dealing with rotational dynamics and motion.
A person who weighs 800 N steps onto a scale that is on the floor of an elevator car. If the elevator accelerates upward at a rate of 5 m/s2, what will the scale read?- a)400 N
- b)800 N
- c)1000 N
- d)1200 N
Correct answer is option 'D'. Can you explain this answer?
A person who weighs 800 N steps onto a scale that is on the floor of an elevator car. If the elevator accelerates upward at a rate of 5 m/s2, what will the scale read?
a)
400 N
b)
800 N
c)
1000 N
d)
1200 N
|
Amrita Chauhan answered |
The person exerts a downward force on the scale, and the scale pushes up on the person with an equal (but opposite) force, FN. Thus, the scale reading is FN, the magnitude of the normal force.
FN – FW = ma ⇒ FN – mg = ma
⇒ FN = ma + mg = m (a + g) = (W/g) (a + g) = (800/10) (10 + 5)
FN = 1200 N
Concurrent force system is the system when:- a)Lines of action of all forces pass through a point
- b)Lines of action of all forces are parallel to each other
- c)Lines of action of all forces lie along same line
- d)Lines of action of all forces are not parallel to each other
Correct answer is option 'A'. Can you explain this answer?
Concurrent force system is the system when:
a)
Lines of action of all forces pass through a point
b)
Lines of action of all forces are parallel to each other
c)
Lines of action of all forces lie along same line
d)
Lines of action of all forces are not parallel to each other
|
|
Sagarika Mukherjee answered |
Collinear Forces: Line of action of all the forces act along the same line.
Coplanar parallel forces: All forces are parallel to each other and lie in a single plane
Coplanar concurrent forces: Line of action of all forces pass through a single point and forces lie in the same plane
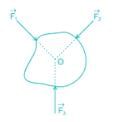
Coplanar non-concurrent forces: All forces do not meet at a point, but lie in a single plane
Non-coplanar parallel forces: All the forces are parallel to each other, but not in same plane
Non-coplanar concurrent forces: All forces do not lie in the same plane, but their lines of action pass through a single point
Non-coplanar non-concurrent forces: All forces do not lie in the same plane and their lines of action do not pass through a single point
The area moment of inertia of a square of size 1 unit about is diagonal is- a)1/3
- b)1/4
- c)1/12
- d)1/6
Correct answer is option 'C'. Can you explain this answer?
The area moment of inertia of a square of size 1 unit about is diagonal is
a)
1/3
b)
1/4
c)
1/12
d)
1/6
|
Simran Saha answered |
For a square of side a, the area moment of inertia of square with respect to one diagonal is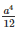 
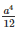
Here a = 1
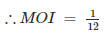
The angular motion of a disc is defined by the relation (θ = 3t + t3), where θ is in radians and t is in seconds. What will be the angular position after 2 seconds?- a)14 rad
- b)12 rad
- c)18 rad
- d)16 rad
Correct answer is option 'A'. Can you explain this answer?
The angular motion of a disc is defined by the relation (θ = 3t + t3), where θ is in radians and t is in seconds. What will be the angular position after 2 seconds?
a)
14 rad
b)
12 rad
c)
18 rad
d)
16 rad
|
|
Pritam Jain answered |
Angular motion θ = 3t + t3
Motion covered in 2 seconds = 3 * 2 + 23 = 14 rad. So the angular position after 2 seconds will be 14 rad.
In case of principal axes of a section _____. - a)Sum of moment of inertia is zero
- b)Difference of moment of inertia is zero
- c)Product of moment of inertia is zero
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
In case of principal axes of a section _____.
a)
Sum of moment of inertia is zero
b)
Difference of moment of inertia is zero
c)
Product of moment of inertia is zero
d)
None of these
|
Sagarika Dey answered |
In principal axes of a section product of inertia is zero.
Product of inertia:- The moment of inertia between any two mutually perpendicular axis in the plane of area is the produce of inertia.
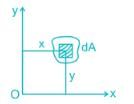
Product of inertia,
Ixy=∫dA.xy
A car moving with uniform acceleration cover 450 m in a 5 second interval, and covers 700 m in the next 5 second interval. The acceleration of the car is- a)7 m/s2
- b)50 m/s2
- c)25 m/s2
- d)10 m/s2
Correct answer is option 'D'. Can you explain this answer?
A car moving with uniform acceleration cover 450 m in a 5 second interval, and covers 700 m in the next 5 second interval. The acceleration of the car is
a)
7 m/s2
b)
50 m/s2
c)
25 m/s2
d)
10 m/s2
|
|
Vaibhav Khanna answered |
Given :
Initial distance of the car (s)= 450 m .
Initial time taken (t)= 5 s .
Initial velocity of the car ( u ) = 450 m / 5 s ⇒ 90 m/s .
Final distance covered by the car = 700 m .
Final time taken by the car = 5 s .
Final velocity of the car ( v )= 700 m / 5 s ⇒ 140 m/s .
Time taken to change the velocity ( t ) = 5 s .
Acceleration is the rate of change of velocity per unit time .
at t = 5 sec, s = 450 m
at t = 10 sec
s = 450 + 700 = 1150
Equation (ii) – Equation (i), we get
a = 10 m/s ^ 2
Hence, Correct answer is D
You can solve such questions and mock tests of Mechanical Engineering by going through the course:
A 50 - kg box rests on horizontal floor for which coefficient of friction is 0.3. If the box is subjected to a horizontal towing force of 400 N, what is its velocity after 5 sec from rest? (Take g = 10 m/s2) - a)40 m/s
- b)30 m/s
- c)27.5 m/s
- d)25 m/s
Correct answer is option 'D'. Can you explain this answer?
A 50 - kg box rests on horizontal floor for which coefficient of friction is 0.3. If the box is subjected to a horizontal towing force of 400 N, what is its velocity after 5 sec from rest? (Take g = 10 m/s2)
a)
40 m/s
b)
30 m/s
c)
27.5 m/s
d)
25 m/s
|
Ananya Saha answered |
Given data:
Mass of the box, m = 50 kg
Coefficient of friction, μ = 0.3
Towing force, F = 400 N
Acceleration due to gravity, g = 10 m/s^2
Time, t = 5 s
To find:
Velocity of the box after 5 seconds from rest
Firstly, we need to calculate the frictional force acting on the box. The frictional force can be found using the equation:
Frictional force, F_friction = μ × Normal force
The normal force acting on the box is equal to the weight of the box, which can be calculated as:
Normal force, N = mg
Where,
m = mass of the box
g = acceleration due to gravity
Substituting the values, we get:
Normal force, N = 50 kg × 10 m/s^2 = 500 N
Now, we can calculate the frictional force:
F_friction = 0.3 × 500 N = 150 N
The net force acting on the box can be found by subtracting the frictional force from the applied force:
Net force, F_net = F - F_friction
Substituting the values, we get:
F_net = 400 N - 150 N = 250 N
Next, we can calculate the acceleration of the box using Newton's second law of motion:
F_net = ma
Substituting the values, we get:
250 N = 50 kg × a
Simplifying, we get:
a = 250 N / 50 kg = 5 m/s^2
Finally, we can calculate the velocity of the box after 5 seconds using the equation of motion:
v = u + at
Where,
v = final velocity
u = initial velocity (0 m/s)
a = acceleration
t = time
Substituting the values, we get:
v = 0 + 5 m/s^2 × 5 s = 25 m/s
Therefore, the velocity of the box after 5 seconds from rest is 25 m/s, which corresponds to option D.
Mass of the box, m = 50 kg
Coefficient of friction, μ = 0.3
Towing force, F = 400 N
Acceleration due to gravity, g = 10 m/s^2
Time, t = 5 s
To find:
Velocity of the box after 5 seconds from rest
Firstly, we need to calculate the frictional force acting on the box. The frictional force can be found using the equation:
Frictional force, F_friction = μ × Normal force
The normal force acting on the box is equal to the weight of the box, which can be calculated as:
Normal force, N = mg
Where,
m = mass of the box
g = acceleration due to gravity
Substituting the values, we get:
Normal force, N = 50 kg × 10 m/s^2 = 500 N
Now, we can calculate the frictional force:
F_friction = 0.3 × 500 N = 150 N
The net force acting on the box can be found by subtracting the frictional force from the applied force:
Net force, F_net = F - F_friction
Substituting the values, we get:
F_net = 400 N - 150 N = 250 N
Next, we can calculate the acceleration of the box using Newton's second law of motion:
F_net = ma
Substituting the values, we get:
250 N = 50 kg × a
Simplifying, we get:
a = 250 N / 50 kg = 5 m/s^2
Finally, we can calculate the velocity of the box after 5 seconds using the equation of motion:
v = u + at
Where,
v = final velocity
u = initial velocity (0 m/s)
a = acceleration
t = time
Substituting the values, we get:
v = 0 + 5 m/s^2 × 5 s = 25 m/s
Therefore, the velocity of the box after 5 seconds from rest is 25 m/s, which corresponds to option D.
A 1.0 kg ball drops vertically onto the floor with a speed of 25 m/s. It rebounds with an initial speed of 10 m/s. The impulse action on the ball during contact will be- a)15 N - s
- b)25 N - s
- c)35 N - s
- d)45 N - s
Correct answer is option 'C'. Can you explain this answer?
A 1.0 kg ball drops vertically onto the floor with a speed of 25 m/s. It rebounds with an initial speed of 10 m/s. The impulse action on the ball during contact will be
a)
15 N - s
b)
25 N - s
c)
35 N - s
d)
45 N - s
|
Dipika Bose answered |
Impulse and Momentum
To understand the solution to this problem, we need to have a clear understanding of impulse and momentum.
- Impulse: Impulse is the product of the force applied to an object and the time interval over which the force is applied. It can be calculated using the equation:
Impulse = Force × Time
- Momentum: Momentum is the product of an object's mass and velocity. It can be calculated using the equation:
Momentum = Mass × Velocity
- Conservation of Momentum: According to the law of conservation of momentum, the total momentum of a system remains constant if no external forces act on it.
Given Parameters
- Mass of the ball (m) = 1.0 kg
- Initial velocity of the ball (u) = 25 m/s
- Final velocity of the ball (v) = -10 m/s (since it rebounds in the opposite direction)
Calculating the Change in Momentum
The change in momentum of the ball can be calculated using the equation:
Change in Momentum = Final Momentum - Initial Momentum
- Initial Momentum = Mass × Initial Velocity = m × u
- Final Momentum = Mass × Final Velocity = m × v
Substituting the given values:
- Initial Momentum = 1.0 kg × 25 m/s = 25 kg·m/s
- Final Momentum = 1.0 kg × (-10 m/s) = -10 kg·m/s
- Change in Momentum = (-10 kg·m/s) - (25 kg·m/s)
Change in Momentum = -35 kg·m/s
Calculating the Impulse
The impulse on the ball during contact can be calculated by equating it to the change in momentum. Therefore:
Impulse = Change in Momentum
Substituting the value of the change in momentum:
Impulse = -35 kg·m/s
Since impulse is a vector quantity, we consider its magnitude. Therefore, the magnitude of the impulse is 35 N·s.
Answer Explanation
The correct answer is option C) 35 N·s. The impulse acting on the ball during contact is 35 N·s.
To understand the solution to this problem, we need to have a clear understanding of impulse and momentum.
- Impulse: Impulse is the product of the force applied to an object and the time interval over which the force is applied. It can be calculated using the equation:
Impulse = Force × Time
- Momentum: Momentum is the product of an object's mass and velocity. It can be calculated using the equation:
Momentum = Mass × Velocity
- Conservation of Momentum: According to the law of conservation of momentum, the total momentum of a system remains constant if no external forces act on it.
Given Parameters
- Mass of the ball (m) = 1.0 kg
- Initial velocity of the ball (u) = 25 m/s
- Final velocity of the ball (v) = -10 m/s (since it rebounds in the opposite direction)
Calculating the Change in Momentum
The change in momentum of the ball can be calculated using the equation:
Change in Momentum = Final Momentum - Initial Momentum
- Initial Momentum = Mass × Initial Velocity = m × u
- Final Momentum = Mass × Final Velocity = m × v
Substituting the given values:
- Initial Momentum = 1.0 kg × 25 m/s = 25 kg·m/s
- Final Momentum = 1.0 kg × (-10 m/s) = -10 kg·m/s
- Change in Momentum = (-10 kg·m/s) - (25 kg·m/s)
Change in Momentum = -35 kg·m/s
Calculating the Impulse
The impulse on the ball during contact can be calculated by equating it to the change in momentum. Therefore:
Impulse = Change in Momentum
Substituting the value of the change in momentum:
Impulse = -35 kg·m/s
Since impulse is a vector quantity, we consider its magnitude. Therefore, the magnitude of the impulse is 35 N·s.
Answer Explanation
The correct answer is option C) 35 N·s. The impulse acting on the ball during contact is 35 N·s.
A man stands on weighing scale in a lift which carries him upwards with acceleration. The reading on the weighing scale will be- a)True weight of the man
- b)Lower than the true weight
- c)Greater than the true weight
- d)Zero
Correct answer is option 'C'. Can you explain this answer?
A man stands on weighing scale in a lift which carries him upwards with acceleration. The reading on the weighing scale will be
a)
True weight of the man
b)
Lower than the true weight
c)
Greater than the true weight
d)
Zero
|
Aditya Patel answered |
Explanation:
When a person stands on a weighing scale in a lift, the reading on the weighing scale is a measure of the normal force exerted by the person on the scale. This normal force is equal to the person's weight in the absence of any acceleration.
However, in this scenario, the lift is accelerating upwards. According to Newton's second law of motion, the net force acting on an object is equal to the mass of the object multiplied by its acceleration. In this case, the net force acting on the person is the difference between the force due to gravity (weight) and the force exerted by the scale (normal force).
Key points:
- The true weight of the person is the force due to gravity acting on the person, which is equal to the person's mass multiplied by the acceleration due to gravity.
- When the lift accelerates upwards, the net force acting on the person is greater than the force due to gravity alone. This is because the normal force exerted by the scale must be greater to counteract the additional force required to accelerate the person upwards.
- The reading on the weighing scale is equal to the normal force exerted by the person on the scale. Since the net force is greater than the force due to gravity, the reading on the scale will be greater than the true weight of the person.
- Therefore, the correct answer is option 'C' - the reading on the weighing scale will be greater than the true weight of the man.
In summary, when a person stands on a weighing scale in a lift that is accelerating upwards, the reading on the scale will be greater than the true weight of the person. This is because the scale must exert a greater normal force to counteract the additional force required to accelerate the person upwards.
When a person stands on a weighing scale in a lift, the reading on the weighing scale is a measure of the normal force exerted by the person on the scale. This normal force is equal to the person's weight in the absence of any acceleration.
However, in this scenario, the lift is accelerating upwards. According to Newton's second law of motion, the net force acting on an object is equal to the mass of the object multiplied by its acceleration. In this case, the net force acting on the person is the difference between the force due to gravity (weight) and the force exerted by the scale (normal force).
Key points:
- The true weight of the person is the force due to gravity acting on the person, which is equal to the person's mass multiplied by the acceleration due to gravity.
- When the lift accelerates upwards, the net force acting on the person is greater than the force due to gravity alone. This is because the normal force exerted by the scale must be greater to counteract the additional force required to accelerate the person upwards.
- The reading on the weighing scale is equal to the normal force exerted by the person on the scale. Since the net force is greater than the force due to gravity, the reading on the scale will be greater than the true weight of the person.
- Therefore, the correct answer is option 'C' - the reading on the weighing scale will be greater than the true weight of the man.
In summary, when a person stands on a weighing scale in a lift that is accelerating upwards, the reading on the scale will be greater than the true weight of the person. This is because the scale must exert a greater normal force to counteract the additional force required to accelerate the person upwards.
An elevator weighing 1000 kg attains an upward velocity of 4 m/sec in two seconds with uniform acceleration. The tension in the supporting cables will be:-- a)1000 N
- b)800 N
- c)1200 N
- d)None of these
Correct answer is option 'D'. Can you explain this answer?
An elevator weighing 1000 kg attains an upward velocity of 4 m/sec in two seconds with uniform acceleration. The tension in the supporting cables will be:-
a)
1000 N
b)
800 N
c)
1200 N
d)
None of these
|
Rajat Basu answered |
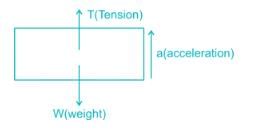
Force = T - W
ma = T - W
Acceleration is given as
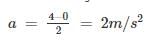
Tension is given as
T = mg + ma = m (g + a)
T = 1000 (10 + 2)
T = 12000 N
If tension in the cable supporting a lift moving downwards is half the tension when it is moving upwards, the acceleration of the lift is- a)g/2
- b)g/3
- c)g/4
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
If tension in the cable supporting a lift moving downwards is half the tension when it is moving upwards, the acceleration of the lift is
a)
g/2
b)
g/3
c)
g/4
d)
None of these
|
|
Pritam Jain answered |
When lift is at rest: T = mg
When lift is accelerating upward: TU = mg + ma
When lift is accelerating downward: TD = mg - ma
TU = 2TD
mg + ma = 2mg - 2ma
a = g/3
Which of the following conditions do not change the effect of couple?- a)Shifting of couple to a new position in its plane
- b)Shifting of couple to a parallel plane
- c)Rotation of couple in its plane
- d)All of the above
Correct answer is option 'D'. Can you explain this answer?
Which of the following conditions do not change the effect of couple?
a)
Shifting of couple to a new position in its plane
b)
Shifting of couple to a parallel plane
c)
Rotation of couple in its plane
d)
All of the above
|
|
Pritam Jain answered |
Two parallel forces equal in magnitude and opposite in direction and separated by a definite distance are said to form a couple.
The translatory effect of a couple on the body is zero.
The only effect of a couple is a moment and this moment is same about any point, the effect of a couple is unchanged if:
(i) The couple is rotated through any plane
(ii) The couple is shifted to any other position
(iii) The couple is replaced by another pair of forces whose rotational effect is same
A rubber ball is dropped from a height of 2 m. If there is not loss of velocity after rebounding the ball will rise to a height of- a)1 m
- b)2 m
- c)3 m
- d)4 m
Correct answer is option 'B'. Can you explain this answer?
A rubber ball is dropped from a height of 2 m. If there is not loss of velocity after rebounding the ball will rise to a height of
a)
1 m
b)
2 m
c)
3 m
d)
4 m
|
|
Stuti Bajaj answered |
Understanding the Problem
When a rubber ball is dropped from a height of 2 meters, it free falls under the influence of gravity. Upon hitting the ground, it rebounds back to a height determined by its initial drop height and its ability to retain energy.
Key Concepts
- Initial Height: The ball is dropped from a height of 2 meters.
- Rebound Behavior: The problem states there is no loss of velocity after rebounding, implying that the ball retains its kinetic energy perfectly.
Energy Conservation
- When the ball is dropped, it converts its potential energy (PE) at the height of 2 meters into kinetic energy (KE) as it falls.
- Upon rebounding, if there is no loss of velocity, the KE is transformed back into PE as the ball rises.
Height Calculation
- At the peak of its rebound, the ball's velocity becomes zero momentarily, and all the kinetic energy converts back to potential energy.
- Hence, if it rebounds without any energy loss, it will rise to the same height from which it was dropped.
Conclusion
- Since the ball was initially dropped from 2 meters and rebounds without losing energy, it will rise back to a height of 2 meters.
- Therefore, the correct answer is option B (2 m).
This analysis shows that the ball's rebound height is equal to its initial drop height when no energy is lost during the rebound.
When a rubber ball is dropped from a height of 2 meters, it free falls under the influence of gravity. Upon hitting the ground, it rebounds back to a height determined by its initial drop height and its ability to retain energy.
Key Concepts
- Initial Height: The ball is dropped from a height of 2 meters.
- Rebound Behavior: The problem states there is no loss of velocity after rebounding, implying that the ball retains its kinetic energy perfectly.
Energy Conservation
- When the ball is dropped, it converts its potential energy (PE) at the height of 2 meters into kinetic energy (KE) as it falls.
- Upon rebounding, if there is no loss of velocity, the KE is transformed back into PE as the ball rises.
Height Calculation
- At the peak of its rebound, the ball's velocity becomes zero momentarily, and all the kinetic energy converts back to potential energy.
- Hence, if it rebounds without any energy loss, it will rise to the same height from which it was dropped.
Conclusion
- Since the ball was initially dropped from 2 meters and rebounds without losing energy, it will rise back to a height of 2 meters.
- Therefore, the correct answer is option B (2 m).
This analysis shows that the ball's rebound height is equal to its initial drop height when no energy is lost during the rebound.
Moment of inertia of an area always least with respect to- a)Bottom-most axis
- b)Radius of gyration
- c)Vertical axis
- d)Centroidal axis
Correct answer is option 'D'. Can you explain this answer?
Moment of inertia of an area always least with respect to
a)
Bottom-most axis
b)
Radius of gyration
c)
Vertical axis
d)
Centroidal axis
|
|
Sagarika Mukherjee answered |
Mass distribution is minimum about centroidal axis, so moment of inertia of an area always least with respect to centroidal axis
A body moves with a speed of 10 m/s in the curved path of 25 m radius of curvature. If the tangential acceleration is 3 m/s2, then total acceleration for the body will be:- a)3.3 m/s2
- b)4 m/s2
- c)5 m/s2
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
A body moves with a speed of 10 m/s in the curved path of 25 m radius of curvature. If the tangential acceleration is 3 m/s2, then total acceleration for the body will be:
a)
3.3 m/s2
b)
4 m/s2
c)
5 m/s2
d)
None of these
|
|
Sagarika Dey answered |
Normal component: an = v2/r = (10)2/(25) = 4
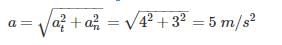
A cannonball is fired from a tower 80 m above the ground with a horizontal velocity of 100 m/s. Determine the horizontal distance at which the ball will hit the ground. (Take g = 10 m/s2)- a)400 m
- b)280 m
- c)200 m
- d)100 m
Correct answer is option 'A'. Can you explain this answer?
A cannonball is fired from a tower 80 m above the ground with a horizontal velocity of 100 m/s. Determine the horizontal distance at which the ball will hit the ground. (Take g = 10 m/s2)
a)
400 m
b)
280 m
c)
200 m
d)
100 m
|
|
Pritam Das answered |
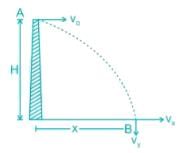
vx = vo = Horizontal component of velocity
vy = Vertical component
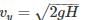
Time taken by the body to cover vertical distance H
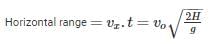
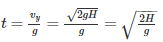
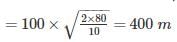
A fan consumes 20 W of electric power and discharges air from a ventilated room at 0.25 kg/s. The maximum air outlet velocity is nearly - a)4.7 m/s
- b)8.7 m/s
- c)10.2 m/s
- d)12.7 m/s
Correct answer is option 'D'. Can you explain this answer?
A fan consumes 20 W of electric power and discharges air from a ventilated room at 0.25 kg/s. The maximum air outlet velocity is nearly
a)
4.7 m/s
b)
8.7 m/s
c)
10.2 m/s
d)
12.7 m/s
|
|
Sagarika Dey answered |
A fan is claimed to increase the velocity of air to a specified value while consuming electric power at a specified rate. The electric power input will be equal to the rate of increase of the kinetic energy of air
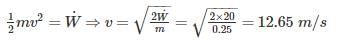
On a ladder resting on a smooth ground and leaning against vertical wall, the force of friction will be:- a)Away from the wall at its upper end
- b)Towards the wall at its upper end
- c)Upwards at its upper end
- d)Downwards at its upper end
Correct answer is option 'C'. Can you explain this answer?
On a ladder resting on a smooth ground and leaning against vertical wall, the force of friction will be:
a)
Away from the wall at its upper end
b)
Towards the wall at its upper end
c)
Upwards at its upper end
d)
Downwards at its upper end
|
|
Gayatri Dasgupta answered |
Free body diagram of a ladder resting on a frictional surface is:
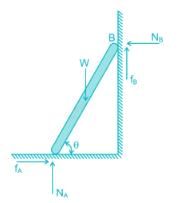
The force of friction will be upwards at its upper end and towards the wall at its lower end.
As the ground is smooth (but the wall does not), so fA = 0 and fB ≠ 0
So the force of friction will be upwards at its upper end.
Which of the following is an example of a body undergoing translational equilibrium?- a)A body at rest on a table
- b)A body travelling in a circular path at a constant speed
- c)A body rotating with constant angular speed about an axis
- d)A body sliding down a frictionless inclined plane
Correct answer is option 'A'. Can you explain this answer?
Which of the following is an example of a body undergoing translational equilibrium?
a)
A body at rest on a table
b)
A body travelling in a circular path at a constant speed
c)
A body rotating with constant angular speed about an axis
d)
A body sliding down a frictionless inclined plane
|
|
Ameya Kaur answered |
Example of a Body Undergoing Translational Equilibrium
Body at Rest on a Table
A body undergoing translational equilibrium is a body in which the net force acting on it is zero, and it is either at rest or moving with a constant velocity in a straight line. One example of such a body is a body at rest on a table. Let's break down the explanation into the following headings:
Definition of Translational Equilibrium
Translational equilibrium is a state in which a body is at rest or moving with a constant velocity in a straight line. It occurs when the net force acting on a body is zero.
Factors Affecting Translational Equilibrium
There are two factors that affect translational equilibrium:
- Net force acting on the body
- Frictional forces acting on the body
In order for a body to be in translational equilibrium, the net force acting on it must be zero. If there is a net force acting on the body, it will either accelerate or decelerate. Additionally, frictional forces must be taken into account. If there is friction between the body and the surface it is resting on, the force of friction will act to oppose any motion of the body.
Body at Rest on a Table
A body at rest on a table is an example of a body undergoing translational equilibrium. The net force acting on the body is zero, and the force of gravity acting downwards is balanced by the normal force of the table acting upwards. Since the body is at rest, it is not accelerating.
Conclusion
In conclusion, a body undergoing translational equilibrium is a body in which the net force acting on it is zero, and it is either at rest or moving with a constant velocity in a straight line. A body at rest on a table is an example of such a body, as the net force acting on it is zero, and it is not accelerating.
Body at Rest on a Table
A body undergoing translational equilibrium is a body in which the net force acting on it is zero, and it is either at rest or moving with a constant velocity in a straight line. One example of such a body is a body at rest on a table. Let's break down the explanation into the following headings:
Definition of Translational Equilibrium
Translational equilibrium is a state in which a body is at rest or moving with a constant velocity in a straight line. It occurs when the net force acting on a body is zero.
Factors Affecting Translational Equilibrium
There are two factors that affect translational equilibrium:
- Net force acting on the body
- Frictional forces acting on the body
In order for a body to be in translational equilibrium, the net force acting on it must be zero. If there is a net force acting on the body, it will either accelerate or decelerate. Additionally, frictional forces must be taken into account. If there is friction between the body and the surface it is resting on, the force of friction will act to oppose any motion of the body.
Body at Rest on a Table
A body at rest on a table is an example of a body undergoing translational equilibrium. The net force acting on the body is zero, and the force of gravity acting downwards is balanced by the normal force of the table acting upwards. Since the body is at rest, it is not accelerating.
Conclusion
In conclusion, a body undergoing translational equilibrium is a body in which the net force acting on it is zero, and it is either at rest or moving with a constant velocity in a straight line. A body at rest on a table is an example of such a body, as the net force acting on it is zero, and it is not accelerating.
Two car A and B moves at 54 Km/hr in the same direction and the car B is 300 m ahead of car A. If the car A is accelerated at 6 m/s2 while car B continue to move with the same velocity, calculate the time taken by car A to overtake car B:- a)10 s
- b)20 s
- c)15 s
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
Two car A and B moves at 54 Km/hr in the same direction and the car B is 300 m ahead of car A. If the car A is accelerated at 6 m/s2 while car B continue to move with the same velocity, calculate the time taken by car A to overtake car B:
a)
10 s
b)
20 s
c)
15 s
d)
None of these
|
|
Siddharth Datta answered |
uA = uB = 54 Km/hr = 15 m/s; aA = 6 m/s2, aB = 0
Car B is 300 m ahead of car A.
Let both move in time t sec.
Distance travelled by A in time t = 300 + Distance travelled by B in time t
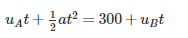
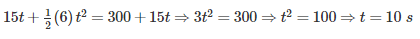
A couple is formed when:- a)Two unequal and unlike parallel force acting on a body
- b)Two unequal and like parallel force acting on a body
- c)Two equal and unlike parallel force acting on a body
- d)Two equal and like parallel force acting on a body
Correct answer is option 'C'. Can you explain this answer?
A couple is formed when:
a)
Two unequal and unlike parallel force acting on a body
b)
Two unequal and like parallel force acting on a body
c)
Two equal and unlike parallel force acting on a body
d)
Two equal and like parallel force acting on a body
|
Nisha Singh answered |
A couple consists of two parallel forces that are equal in magnitude, opposite in sense and do not share a line of action. It does not produce any translation, only rotation. The resultant force of a couple is zero. But, the resultant of a couple is not zero; it is a pure moment.
Two forces of 30 N and 40 N are acting at 90° to each other, the resultant force is- a)70 N
- b)35 N
- c)20 N
- d)None of these
Correct answer is option 'D'. Can you explain this answer?
Two forces of 30 N and 40 N are acting at 90° to each other, the resultant force is
a)
70 N
b)
35 N
c)
20 N
d)
None of these
|
|
Nitin Joshi answered |
Resultant between two forces P and Q, acting at an angle θ is defined as:
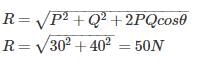
If v1 and v2 are the initial velocities of two bodies making direct collision and if u1 and u2 are their respective velocities after collision then the coefficient of restitution is given by:- a)
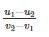
- b)
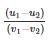
- c)
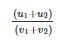
- d)
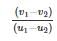
Correct answer is option 'A'. Can you explain this answer?
If v1 and v2 are the initial velocities of two bodies making direct collision and if u1 and u2 are their respective velocities after collision then the coefficient of restitution is given by:
a)
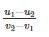
b)
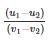
c)
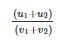
d)
|
|
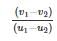
Divya Banerjee answered |
The energy dissipation during impact is called by the term, coefficient of restitution, a scalar quantity
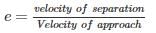
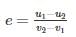
A body of mass 10 kg moving with a velocity of 1 m/s is acted upon by a force of 50 N for two seconds. The final velocity will be:- a)22 m/sec
- b)10 m/sec
- c)
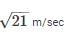
- d)11 m/sec
Correct answer is option 'D'. Can you explain this answer?
A body of mass 10 kg moving with a velocity of 1 m/s is acted upon by a force of 50 N for two seconds. The final velocity will be:
a)
22 m/sec
b)
10 m/sec
c)
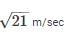
d)
11 m/sec
|
|
Tarun Chatterjee answered |
Velocity = mass × acceleration
∴ 50 = 10 × a
⇒ a = 5 m/sec2
Velocity after 2 seconds,
v = u + at
= 1 + 5 × 2
= 11 m/sec
Which of the following forces have zero value of resultant?- a)Non - concurrent forces
- b)Non - coplanar forces
- c)Coplanar forces
- d)Equilibrium forces
Correct answer is option 'D'. Can you explain this answer?
Which of the following forces have zero value of resultant?
a)
Non - concurrent forces
b)
Non - coplanar forces
c)
Coplanar forces
d)
Equilibrium forces
|
|
Prateek Mukherjee answered |
Equilibrium is the status of the body when it is subjected to a system of forces. If the resultant force is equal to zero it implies that the net effect of the system of forces is zero this represents the state of equilibrium.
The angular velocity (in radians /sec) of a body rotating at N rpm is:- a)
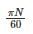
- b)
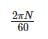
- c)
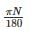
- d)
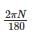
Correct answer is option 'B'. Can you explain this answer?
The angular velocity (in radians /sec) of a body rotating at N rpm is:
a)
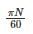
b)
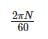
c)
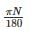
d)
|
|
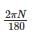
Ameya Kaur answered |
Rpm is just a measure of how many times a point is revolving per minute.
In a single revolution, a point rotates an angle = 2π
So, the total angle a point is rotating per minute = N x 2 π
The angular velocity is a measure of how fast it is rotating = Angle Rotated/Time Required = 2π N/60
Two rings of radius R and nR, made up of same material (linear mass density) have the ratio of moment of inertia about an axis passing through centre as 1 : 8. The value of n is- a)2
- b)1/4
- c)4
- d)1/2
Correct answer is option 'A'. Can you explain this answer?
Two rings of radius R and nR, made up of same material (linear mass density) have the ratio of moment of inertia about an axis passing through centre as 1 : 8. The value of n is
a)
2
b)
1/4
c)
4
d)
1/2
|
|
Pritam Jain answered |
For ring:
MOI about diametric axis: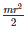 
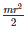
MOI about polar axis: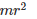 
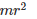
Linear mass density:
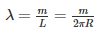
m=λ×2πR
n = 2
The sum of kinetic and potential energy of a falling body _____.- a)Is constant at all points
- b)Varies from point to point
- c)Is maximum at starting and goes on increasing
- d)Is maximum at starting and goes on decreasing
Correct answer is option 'A'. Can you explain this answer?
The sum of kinetic and potential energy of a falling body _____.
a)
Is constant at all points
b)
Varies from point to point
c)
Is maximum at starting and goes on increasing
d)
Is maximum at starting and goes on decreasing
|
|
Anjali Sengupta answered |
Kinetic energy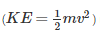 
represents energy the mass possesses by virtue of its motion. Likewise, potential energy (PE=mgh) represents energy the mass possesses by virtue of its position.
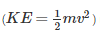represents energy the mass possesses by virtue of its motion. Likewise, potential energy (PE=mgh) represents energy the mass possesses by virtue of its position.E=KE+PE
E is the total energy of the mass: i.e., the sum of its kinetic and potential energies. It is clear that E is a conserved quantity: i.e., although the kinetic and potential energies of the mass vary as it falls, its total energy remains the same and one form of energy is being converted into other form of energy.
A ball of mass 1 kg moving with the velocity of 2 m/s collide directly with another stationary ball of mass 2 kg and comes to rest after impact. The velocity of second baII after impact is:- a)Zero
- b)0.5 m/s
- c)1.0 m/s
- d)2.0 m/s
Correct answer is option 'C'. Can you explain this answer?
A ball of mass 1 kg moving with the velocity of 2 m/s collide directly with another stationary ball of mass 2 kg and comes to rest after impact. The velocity of second baII after impact is:
a)
Zero
b)
0.5 m/s
c)
1.0 m/s
d)
2.0 m/s
|
|
Vaibhav Khanna answered |
Conservation of linear momentum: 
For maximum horizontal range, the angle of projection of a projectile should be- a)30°
- b)45°
- c)60°
- d)90°
Correct answer is option 'B'. Can you explain this answer?
For maximum horizontal range, the angle of projection of a projectile should be
a)
30°
b)
45°
c)
60°
d)
90°
|
|
Soumya Basak answered |
Horizontal range,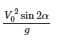 
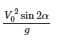
For maximum horizontal range.
Sin 2α = 1
Or 2α = 90°
Or α = 45°
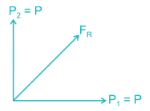
A barge is pulled by two tugboats as shown in the figure below. The resultant of forces exerted by the tugboats is 1000 kg force. What will be the value of θ so that tension in rope 2 is minimum?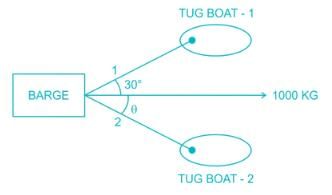
- a)30°
- b)45°
- c)60°
- d)0°
Correct answer is option 'C'. Can you explain this answer?
A barge is pulled by two tugboats as shown in the figure below. The resultant of forces exerted by the tugboats is 1000 kg force. What will be the value of θ so that tension in rope 2 is minimum?
a)
30°
b)
45°
c)
60°
d)
0°
|
|
Sagarika Dey answered |
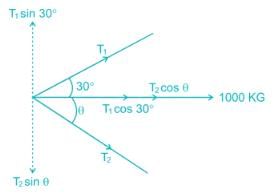
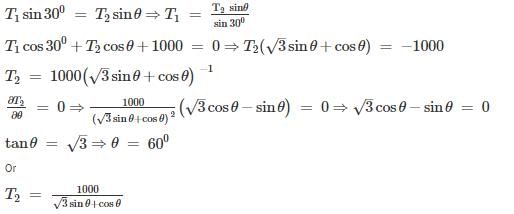
By taking the values of θ, given in the options we can conclude that for θ = 600, T2 is minimum.
Chapter doubts & questions for Engineering Mechanics - Mechanical Engineering SSC JE (Technical) 2025 is part of Mechanical Engineering exam preparation. The chapters have been prepared according to the Mechanical Engineering exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Mechanical Engineering 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Engineering Mechanics - Mechanical Engineering SSC JE (Technical) in English & Hindi are available as part of Mechanical Engineering exam.
Download more important topics, notes, lectures and mock test series for Mechanical Engineering Exam by signing up for free.
Mechanical Engineering SSC JE (Technical)
6 videos|104 docs|59 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily