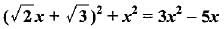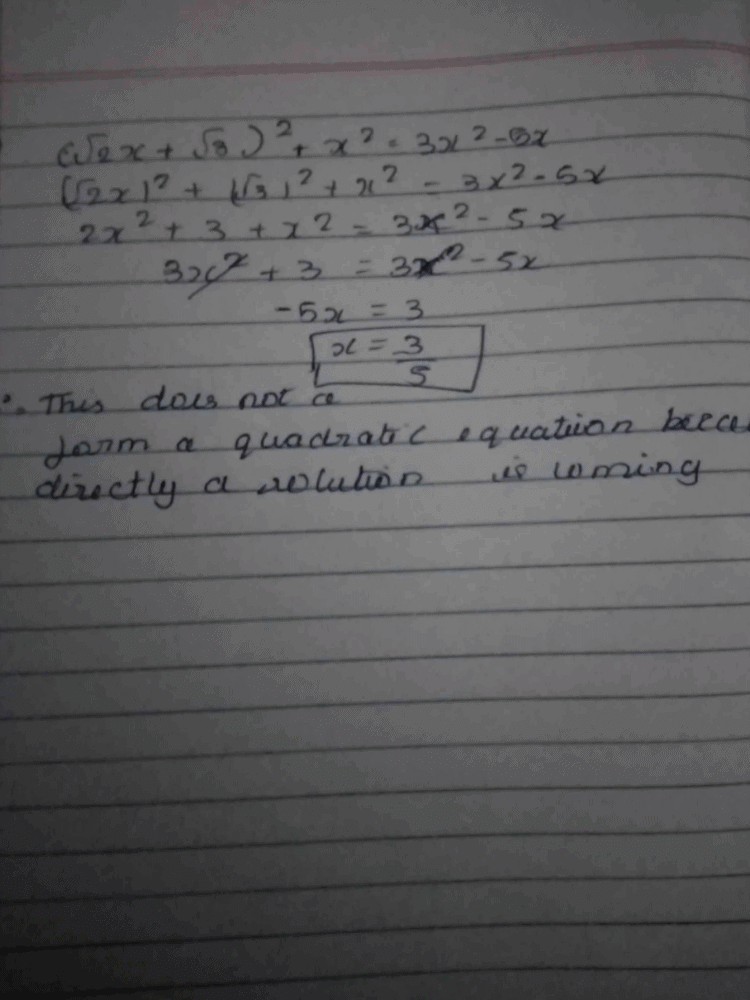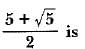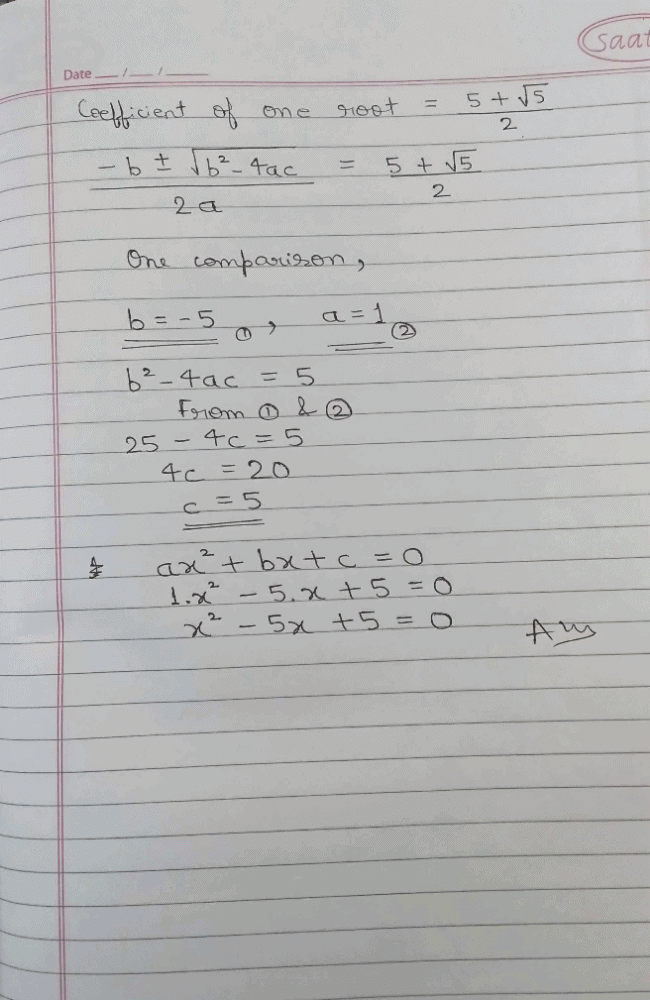All Exams >
BMAT >
Mathematics for BMAT (Section 2) >
All Questions
All questions of Algebra for BMAT Exam
Solve 9x2 = 36- a)±2
- b)±6
- c)±4
- d)2
Correct answer is option 'A'. Can you explain this answer?
Solve 9x2 = 36
a)
±2
b)
±6
c)
±4
d)
2
|
Nilanjan Shah answered |
Solution:
To solve this equation, we need to isolate the variable x.
Given equation is 9x2 = 36
Step 1: Divide both sides by 9
9x2/9 = 36/9
Step 2: Simplify
x2 = 4
Step 3: Take square root on both sides
√(x2) = √4
Step 4: Simplify
x = ±2
Therefore, the solution of the given equation 9x2 = 36 is x = ±2.
Explanation:
The given equation is a quadratic equation in which we need to find the value of x. To solve the equation, we need to isolate the variable x by following the steps mentioned above. We divided both sides by 9 to simplify the equation. After simplification, we got x2 = 4 which means x can be either positive or negative 2. We took the square root of both sides and simplified the equation to get the final solution x = ±2.
To solve this equation, we need to isolate the variable x.
Given equation is 9x2 = 36
Step 1: Divide both sides by 9
9x2/9 = 36/9
Step 2: Simplify
x2 = 4
Step 3: Take square root on both sides
√(x2) = √4
Step 4: Simplify
x = ±2
Therefore, the solution of the given equation 9x2 = 36 is x = ±2.
Explanation:
The given equation is a quadratic equation in which we need to find the value of x. To solve the equation, we need to isolate the variable x by following the steps mentioned above. We divided both sides by 9 to simplify the equation. After simplification, we got x2 = 4 which means x can be either positive or negative 2. We took the square root of both sides and simplified the equation to get the final solution x = ±2.
Using identity (x − a) (x + a) = x2− a2 find 62− 52. - a)11
- b)12
- c)10
- d)none of these
Correct answer is 'A'. Can you explain this answer?
Using identity (x − a) (x + a) = x2− a2 find 62− 52.
a)
11
b)
12
c)
10
d)
none of these
|
Rahul Kumar answered |
To find: 62 - 52:
Putting x = 6 and a = 5 in identity x2 - a2 = (x - a)(x+a);
⇒ 62- 52 = (6 - 5)(6 + 5) = 11.
Which of the following is an expression?- a)10
- b)3
- c)1/2
- d)4x + 7
Correct answer is option 'D'. Can you explain this answer?
Which of the following is an expression?
a)
10
b)
3
c)
1/2
d)
4x + 7
|
Amit Sharma answered |
An algebraic expression include constants, variables and coefficients, so answer is 4x+7
The two consecutive odd positive integers, sum of whose squares is 290 are- a)13, 15
- b)11, 13
- c)7, 9
- d)5, 7
Correct answer is option 'B'. Can you explain this answer?
The two consecutive odd positive integers, sum of whose squares is 290 are
a)
13, 15
b)
11, 13
c)
7, 9
d)
5, 7
|
|
Drishti Kumari answered |
Let first consecutive odd positive integer be x
Secon = x + 2
(x)^2 + ( x + 2 )^2 = 290
x^2 + x^2 + 4 + 4x = 290
2x^2 + 4x = 290 - 4
2x^2 + 4x = 286
2x^2 + 4x - 286 = 0
x^2 + 2x - 143 = 0
x^2 + 13x - 11x - 143 = 0
x ( x + 13 ) - 11 ( x + 13 ) = 0
( x -11) ( x + 13) = 0
x = 11 Or x = -13
Second = 11 + 2 = 13
Hence option (B) is correct .
Expression that contains only one term is called a __________.- a)monomial
- b)binomial
- c)trinomial
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
Expression that contains only one term is called a __________.
a)
monomial
b)
binomial
c)
trinomial
d)
None of these
|
Pranav Chauhan answered |
Monomial
A monomial is a mathematical expression that contains only one term. It is a type of polynomial that consists of a single term. The term can be a constant, a variable, or a product of constants and variables.
Examples of monomials:
- 5
- x
- 2xy
- -3a²
A monomial can be simplified by combining like terms. Like terms are terms that have the same variables raised to the same powers.
For example, the monomial 3x²y - 2xy² can be simplified as follows:
3x²y - 2xy² = xy(3x - 2y)
In this simplified form, the monomial is still a single term, but it is expressed as a product of a constant (xy) and a binomial (3x - 2y).
Binomial and Trinomial
Binomials and trinomials are also types of polynomials, but they contain two and three terms, respectively.
Examples of binomials:
- 2x + 5y
- 3a² - 4b
- 6xy + 2y²
Examples of trinomials:
- x² + 2x + 1
- 2a² - 5ab + 3b²
- 4xy² + 3x²y - 2y³
A monomial is a mathematical expression that contains only one term. It is a type of polynomial that consists of a single term. The term can be a constant, a variable, or a product of constants and variables.
Examples of monomials:
- 5
- x
- 2xy
- -3a²
A monomial can be simplified by combining like terms. Like terms are terms that have the same variables raised to the same powers.
For example, the monomial 3x²y - 2xy² can be simplified as follows:
3x²y - 2xy² = xy(3x - 2y)
In this simplified form, the monomial is still a single term, but it is expressed as a product of a constant (xy) and a binomial (3x - 2y).
Binomial and Trinomial
Binomials and trinomials are also types of polynomials, but they contain two and three terms, respectively.
Examples of binomials:
- 2x + 5y
- 3a² - 4b
- 6xy + 2y²
Examples of trinomials:
- x² + 2x + 1
- 2a² - 5ab + 3b²
- 4xy² + 3x²y - 2y³
Write the general form of a quadratic polynomia- a)ax2 + bx + c where a, b and c are real numbers
- b)ax2 + bx + c=0
- c)ax2 + bx + c where a, b and c are real numbers and a is not equal to zero.
- d)ax2 + bx + c or bx + ax2 + c or c+ bx + ax2
Correct answer is option 'C'. Can you explain this answer?
Write the general form of a quadratic polynomia
a)
ax2 + bx + c where a, b and c are real numbers
b)
ax2 + bx + c=0
c)
ax2 + bx + c where a, b and c are real numbers and a is not equal to zero.
d)
ax2 + bx + c or bx + ax2 + c or c+ bx + ax2
|
Krishna Iyer answered |
If the coefficient of x2 is zero , then the equation is not a quadratic equation , its a linear equation. So its necessary condition for the quadratic equation.
Which of the following in not a quadratic equation:- a)(x – 2)2 + 1 = 2x – 3
- b)(x + 2)2 = x3 – 4
- c)x(2x + 3) = x2 + 1
- d)x(x + 1) + 8 = (x + 2) (x – 2)
Correct answer is option 'D'. Can you explain this answer?
Which of the following in not a quadratic equation:
a)
(x – 2)2 + 1 = 2x – 3
b)
(x + 2)2 = x3 – 4
c)
x(2x + 3) = x2 + 1
d)
x(x + 1) + 8 = (x + 2) (x – 2)
|
|
Rahul Kumar answered |
Option (B) and (D) , both are the correct answers. We have x(x + 1) + 8 = (x + 2) (x – 2)
=x2 + x + 8 = x2 - 4
= x = -12, which is not a quadratic equation
Also, in (B) (x + 2)2 = x3 – 4
=x2 +4x + 4=x3 - 4, which is a cubic equation
=x2 + x + 8 = x2 - 4
= x = -12, which is not a quadratic equation
Also, in (B) (x + 2)2 = x3 – 4
=x2 +4x + 4=x3 - 4, which is a cubic equation
Can you explain the answer of this question below: If 4 is a root of the equation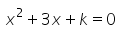 
, then k is
- A:
-28
- B:
-12
- C:
12
- D:
28
The answer is a.
If 4 is a root of the equation , then k is
-28
-12
12
28
|
Vp Classes answered |
4 is the solution , this means that if we put x=4 we get 0. So putting x=4 in the equation x2+3x+k=0 we get 42+3*4+k=0
16+12+k=0 ⇒ k=-28
16+12+k=0 ⇒ k=-28
Which of the following is like term as 7xy?- a)9
- b)9x
- c)9y
- d)9xy
Correct answer is 'D'. Can you explain this answer?
Which of the following is like term as 7xy?
a)
9
b)
9x
c)
9y
d)
9xy
|
Geetika Shah answered |
9xy is the like term of 7xy as ...9xy and 7xy contains the same variable (xy).. if we have to find like terms then.. we we should see that they both contains same variable ..numbers doesn't matter ..they can be sake itlr different.. therefore 9xy is the like term of 7xy and visa versa..
If x = 1 is a common root of the equation x2 + ax – 3 = 0 and bx2 – 7x + 2 = 0 then ab =
- a)10
- b)-3
- c)6
- d)7
Correct answer is option 'A'. Can you explain this answer?
If x = 1 is a common root of the equation x2 + ax – 3 = 0 and bx2 – 7x + 2 = 0 then ab =
a)
10
b)
-3
c)
6
d)
7
|
Zachary Foster answered |
Given:
- x = 1 is a common root of the equations:
- x² + ax - 3 = 0
- bx² - 7x + 2 = 0
To find:
- The value of ab.
Solution:
Since x = 1 is a root of both equations, we can substitute x = 1 in both equations.
Equation 1:
- 1² + a(1) - 3 = 0
- 1 + a - 3 = 0
- a = 2
Equation 2:
- b(1)² - 7(1) + 2 = 0
- b - 7 + 2 = 0
- b = 5
Therefore, ab = 2 * 5 = 10
So, the value of ab is 10.
Using identity (x - a) (x + a) = x2 - a2 find 52− 42.- a)12
- b)14
- c)9
- d)none of these
Correct answer is 'C'. Can you explain this answer?
Using identity (x - a) (x + a) = x2 - a2 find 52− 42.
a)
12
b)
14
c)
9
d)
none of these
|
Gunjan Lakhani answered |
x2 - a2 = ( x + a) (x - a) using this equation.
52 - 42 = ( 5 + 4) ( 5 - 4 )= ( 9 ) (1 )= 9
Multiplication of pq+qr+rp and ‘zero’ is- a)pq+qr
- b)pq+rp
- c)pq+qr+rp
- d)0
Correct answer is option 'D'. Can you explain this answer?
Multiplication of pq+qr+rp and ‘zero’ is
a)
pq+qr
b)
pq+rp
c)
pq+qr+rp
d)
0
|
|
Àrpita țřipathi answered |
Pq+qr+rp,0
=(pq+qr+rp)
=0
/(because 0×anything =is always zero)
The value/s of x when (x – 4) (3x + 2) = 0 ________- a)4, -2/3
- b)-4, – 2/ 3
- c)4, 2/3
- d)-4, 2/3
Correct answer is option 'A'. Can you explain this answer?
The value/s of x when (x – 4) (3x + 2) = 0 ________
a)
4, -2/3
b)
-4, – 2/ 3
c)
4, 2/3
d)
-4, 2/3
|
|
Drishti Kumari answered |
( x - 4 ) ( 3x + 2 ) = 0
x - 4 = 0
x = 4
3x + 2 = 0
3x = -2
x = -2 / 3
Therefore option (A) is correct.
x - 4 = 0
x = 4
3x + 2 = 0
3x = -2
x = -2 / 3
Therefore option (A) is correct.
Terms are added to form ___________.- a)expressions
- b)terms
- c)identities
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
Terms are added to form ___________.
a)
expressions
b)
terms
c)
identities
d)
none of these
|
|
Ritu Joshi answered |
A term can be a signed number, a variable, or a constant multiplied by a variable or variables. Each term in an
Value(s) of k for which the quadratic equation 2x2 -kx + k = 0 has equal roots is
- a)0
- b)4
- c)8
- d)0 and 8
Correct answer is option 'D'. Can you explain this answer?
Value(s) of k for which the quadratic equation 2x2 -kx + k = 0 has equal roots is
a)
0
b)
4
c)
8
d)
0 and 8
|
|
Kuldeep Kuldeep answered |
Solution:-
Compare given Quadratic equation 2x²-kx+k=0 with ax²+bx+c=0, we get
a = 2,
b = -k ,
c = k,
Discriminant (D) = 0
[ Given roots are equal ]
=> b²-4ac = 0
=> (-k)²-4×2×k=0
=> k²-8k=0
=> k(k-8)=0
=> k = 0 or k=8.
So, option d is correct.
Compare given Quadratic equation 2x²-kx+k=0 with ax²+bx+c=0, we get
a = 2,
b = -k ,
c = k,
Discriminant (D) = 0
[ Given roots are equal ]
=> b²-4ac = 0
=> (-k)²-4×2×k=0
=> k²-8k=0
=> k(k-8)=0
=> k = 0 or k=8.
So, option d is correct.
Which of the following is not a quadratic equation ?- a)5x + 3y2 = 0
- b)z2 - 2z = 0
- c)3x + 4 - 7x2 = 0
- d)5x2 - 125 = 0
Correct answer is option 'A'. Can you explain this answer?
Which of the following is not a quadratic equation ?
a)
5x + 3y2 = 0
b)
z2 - 2z = 0
c)
3x + 4 - 7x2 = 0
d)
5x2 - 125 = 0
|
|
Priyanshu Intelligent answered |
In equation first there are two variables.
That's why it is not a quadratic equation.
That's why it is not a quadratic equation.
The two positive numbers differ by 5 and square of their sum is 169 are
- a)2,4
- b)5,6
- c)4,9
- d)3,7
Correct answer is option 'C'. Can you explain this answer?
The two positive numbers differ by 5 and square of their sum is 169 are
a)
2,4
b)
5,6
c)
4,9
d)
3,7
|
Apoorv khanna answered |
Explanation:
Let the two numbers be x and y, where x is greater than y.
Given, x - y = 5
=> x = y + 5
Also, (x+y)^2 = 169
=> (y+5+y)^2 = 169 (Substituting x = y + 5)
=> (2y+5)^2 = 169
=> 4y^2 + 20y + 25 = 169 (Expanding the square)
=> 4y^2 + 20y - 144 = 0
=> y^2 + 5y - 36 = 0
=> (y + 9)(y - 4) = 0
=> y = -9 or y = 4
Since the numbers are positive, y = 4
Therefore, x = y + 5 = 9
Hence, the two numbers are 4 and 9.
Therefore, option C is the correct answer.
Let the two numbers be x and y, where x is greater than y.
Given, x - y = 5
=> x = y + 5
Also, (x+y)^2 = 169
=> (y+5+y)^2 = 169 (Substituting x = y + 5)
=> (2y+5)^2 = 169
=> 4y^2 + 20y + 25 = 169 (Expanding the square)
=> 4y^2 + 20y - 144 = 0
=> y^2 + 5y - 36 = 0
=> (y + 9)(y - 4) = 0
=> y = -9 or y = 4
Since the numbers are positive, y = 4
Therefore, x = y + 5 = 9
Hence, the two numbers are 4 and 9.
Therefore, option C is the correct answer.
Which of the following is a binomial?
- a)7 – 3x + 4
- b)2x + 7
- c)4x + y + 2
- d)3x
Correct answer is option 'B'. Can you explain this answer?
Which of the following is a binomial?
a)
7 – 3x + 4
b)
2x + 7
c)
4x + y + 2
d)
3x
|
C K Academy answered |
2x + 7
A binomial is a mathematical expression consisting of two terms. In this case, 2x + 7 is a binomial because it has two terms: 2x and 7.
- 7 – 3x + 4 is not a binomial because it has three terms: 7, -3x, and 4
- 4x + y + 2 is not a binomial because it has three terms: 4x, y, and 2
- 3x is not a binomial because it has only one term: 3x
The value of q if x = 2 is a solution of 8x2 + qx – 4 = 0 is _____- a)14
- b)-28
- c)-14
- d)28
Correct answer is option 'C'. Can you explain this answer?
The value of q if x = 2 is a solution of 8x2 + qx – 4 = 0 is _____
a)
14
b)
-28
c)
-14
d)
28
|
|
Kuldeep Raj answered |
Let us place 2 in the place of "x" for 8x² + qx - 4 = 0 (According to the question).
8(2)² + q(2) - 4 = 0.
8(4) + 2q - 4 = 0.
32 + 2q - 4 = 0.
Shift (32) to the right side.
2q - 4 = -32.
Shift (-4) to the right side. Then,
2q = -32 + 4.
2q = -28.
q = -28/2.
q = -14.
Therefore, the value of q if x = 2 is a solution of 8x² + qx - 4 = 0 is -14.
Hence, option (c) is correct friend...
8(2)² + q(2) - 4 = 0.
8(4) + 2q - 4 = 0.
32 + 2q - 4 = 0.
Shift (32) to the right side.
2q - 4 = -32.
Shift (-4) to the right side. Then,
2q = -32 + 4.
2q = -28.
q = -28/2.
q = -14.
Therefore, the value of q if x = 2 is a solution of 8x² + qx - 4 = 0 is -14.
Hence, option (c) is correct friend...
The solution of x2 + 4x + 4 = 0 is- a)2
- b)-2
- c)0
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
The solution of x2 + 4x + 4 = 0 is
a)
2
b)
-2
c)
0
d)
None of these
|
|
Priyanshu Intelligent answered |
(-2)^2 + 4(-2) + 4
= 4 - 8 + 4
=8-8
=0.
Hence , option b) is the right answer.
= 4 - 8 + 4
=8-8
=0.
Hence , option b) is the right answer.
If p,q and r are rational numbers and p ≠ q ≠ r, then roots of the equation (p2 - q2)x2 - (q2 - r2)x + (r2 - p2) = 0 are- a)
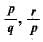
- b)
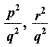
- c)
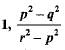
- d)
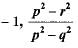
Correct answer is option ''. Can you explain this answer?
If p,q and r are rational numbers and p ≠ q ≠ r, then roots of the equation (p2 - q2)x2 - (q2 - r2)x + (r2 - p2) = 0 are
a)
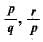
b)
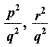
c)
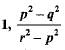
d)
|
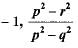
Let's Tute answered |
Putting x = - 1, we have
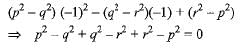∴ x = - 1 is one root.
Only option (d) has one root - 1.
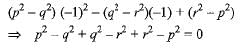∴ x = - 1 is one root.Only option (d) has one root - 1.
If one root of a Quadratic equation is m + , then the other root is- a)m – √n
- b)m +√n
- c)Can not be determined
- d)√m + n
Correct answer is option 'A'. Can you explain this answer?
If one root of a Quadratic equation is m + , then the other root is
a)
m – √n
b)
m +√n
c)
Can not be determined
d)
√m + n
|
|
Arun Sharma answered |
In a quadratic equation with rational coefficients has an irrational root α + √β, then it has a conjugate root α - √β.
So if the root is m+ √n the other root will be m- √n
So if the root is m+ √n the other root will be m- √n
The roots of x2 – 8x + 12 = 0, are- a)x = 0
- b)no real roots
- c)real and unequal
- d)real and equal
Correct answer is option 'C'. Can you explain this answer?
The roots of x2 – 8x + 12 = 0, are
a)
x = 0
b)
no real roots
c)
real and unequal
d)
real and equal
|
|
Shweta singh answered |
The roots of the equation x^2 are x = 0.
If the area of a rectangle is 24 m2 and its perimeter is 20 m, the equation to find its length and breadth would be:
- a)x2 – 10x + 24 = 0
- b)x2 + 1 2x + 24 = 0
- c)x2 – 10x – 24 = 0
- d)x2 + 10x + 28 = 0
Correct answer is option 'A'. Can you explain this answer?
If the area of a rectangle is 24 m2 and its perimeter is 20 m, the equation to find its length and breadth would be:
a)
x2 – 10x + 24 = 0
b)
x2 + 1 2x + 24 = 0
c)
x2 – 10x – 24 = 0
d)
x2 + 10x + 28 = 0
|
|
Aashu Mehra answered |
Perimeter = 2(l+b)=20
l+b=10
lxb=24
so correct option is A
If a,b,c are real and b2-4ac >0 then roots of equation are- a)real roots
- b)real and equal
- c)real and unequal
- d)No real roots
Correct answer is option 'C'. Can you explain this answer?
If a,b,c are real and b2-4ac >0 then roots of equation are
a)
real roots
b)
real and equal
c)
real and unequal
d)
No real roots
|
Ram trivedi answered |
The expression b^2 - 4ac is the discriminant of a quadratic equation of the form ax^2 + bx + c = 0. It determines the nature of the solutions of the equation.
If b^2 - 4ac > 0, then the quadratic equation has two distinct real solutions.
If b^2 - 4ac = 0, then the quadratic equation has one real solution (also known as a double root).
If b^2 - 4ac < 0,="" then="" the="" quadratic="" equation="" has="" no="" real="" solutions.="" however,="" it="" may="" have="" two="" complex="" />
So, in summary, if b^2 - 4ac > 0, there are two real solutions.
If b^2 - 4ac > 0, then the quadratic equation has two distinct real solutions.
If b^2 - 4ac = 0, then the quadratic equation has one real solution (also known as a double root).
If b^2 - 4ac < 0,="" then="" the="" quadratic="" equation="" has="" no="" real="" solutions.="" however,="" it="" may="" have="" two="" complex="" />
So, in summary, if b^2 - 4ac > 0, there are two real solutions.
The condition for equation ax2 + bx + c = 0 to be linear is- a)a > 0, b = 0
- b)a ≠ 0, b = 0
- c)a < 0, b = 0
- d)a = 0, b ≠ 0
Correct answer is option 'D'. Can you explain this answer?
The condition for equation ax2 + bx + c = 0 to be linear is
a)
a > 0, b = 0
b)
a ≠ 0, b = 0
c)
a < 0, b = 0
d)
a = 0, b ≠ 0
|
|
Tanisha answered |
Answer is d...bcoz to make ax^2 +bx+c=0,linear equation.
we need to eliminate ax^2.
So, we will put a=0 ,to make the degree of this equation 1 ...and b should not be equal to 0,bcoz if b will be 0 ,then it will be a constant equation,instead of a linear equation.
we need to eliminate ax^2.
So, we will put a=0 ,to make the degree of this equation 1 ...and b should not be equal to 0,bcoz if b will be 0 ,then it will be a constant equation,instead of a linear equation.
Add: 7xy + 5yz – 3zx, 4yz + 9zx – 4y , –3xz + 5x – 2xy.- a)5xy + 3zx + 5x – 4y
- b)5xy + 9yz +2zx + 5x – 4y
- c)5xy + 9yz +3zx + 5x – 4y
- d)5xy + 9yz +3zx + 4y
Correct answer is option 'C'. Can you explain this answer?
Add: 7xy + 5yz – 3zx, 4yz + 9zx – 4y , –3xz + 5x – 2xy.
a)
5xy + 3zx + 5x – 4y
b)
5xy + 9yz +2zx + 5x – 4y
c)
5xy + 9yz +3zx + 5x – 4y
d)
5xy + 9yz +3zx + 4y
|
|
Sarita Verma answered |
Writing the three expressions in separate rows, with like terms one below the other, we have
7xy + 5yz – 3zx
+ 4yz + 9zx – 4y
+ –2xy – 3zx + 5x
-----------------------------------------
= 5xy + 9yz + 3zx + 5x – 4y
Thus, the sum of the expressions is 5xy + 9yz + 3zx + 5x – 4y. Note how the terms, – 4y
in the second expression and 5x in the third expression, are carried over as they are, since
they have no like terms in the other expressions.
The equation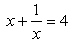 
in standard form ax2 + bx + c = 0 is written as :- a)x2 - 4x + 1 = 0
- b)x2 + 4x + 1 = 0
- c)x2 - 4x - 1 = 0
- d)x2 + 4x - 1 = 0
Correct answer is option 'A'. Can you explain this answer?
The equation 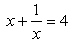in standard form ax2 + bx + c = 0 is written as :
in standard form ax2 + bx + c = 0 is written as :a)
x2 - 4x + 1 = 0
b)
x2 + 4x + 1 = 0
c)
x2 - 4x - 1 = 0
d)
x2 + 4x - 1 = 0
|
Naina Sharma answered |
We have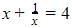 
Taking LCM,
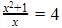
Multiplying LHS and RHS by x
x2+1=4x
x2-4x+1=0
Which is the required equation.
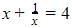
Taking LCM,
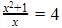
Multiplying LHS and RHS by x
x2+1=4x
x2-4x+1=0
Which is the required equation.
The solution of 5z2 = 3z is- a)0, 3/5
- b)0, -3/5
- c)3/5
- d)0
Correct answer is option 'A'. Can you explain this answer?
The solution of 5z2 = 3z is
a)
0, 3/5
b)
0, -3/5
c)
3/5
d)
0
|
Vikram Kapoor answered |
We have 5z2=3z
5z2-3z=0
z(5z-3)=0
So either z=0
Or 5z-3 =0 = z=⅗. So there are two solutions
5z2-3z=0
z(5z-3)=0
So either z=0
Or 5z-3 =0 = z=⅗. So there are two solutions
Which of the following are the roots of the quadratic equation, x2 - 9x + 20 = 0 by factorisation?- a)3,4
- b)4, 5
- c)5, 6
- d)6, 7
Correct answer is option 'B'. Can you explain this answer?
Which of the following are the roots of the quadratic equation, x2 - 9x + 20 = 0 by factorisation?
a)
3,4
b)
4, 5
c)
5, 6
d)
6, 7
|
|
Gaurav Kumar answered |
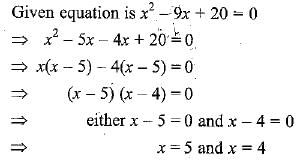
∴ x = 4 and 5 are the roots/solution of the given quadratic equation
Which of the following statement is TRUE?
- a)A quadratic equation in variable x is of the form ax2 + bx + c = 0, where a, b, c are real numbers a ≠ o.
- b)If we can factorise ax2 + bx + c, a ≠ 0 into product of two linear factors then roots can be found by equating each factor to zero
- c)A real number R is said to be a root of the quadratic equation ax2 + bx + c = 0 if a(R)2 + bR + c = 0.
- d)All the above
Correct answer is option 'D'. Can you explain this answer?
Which of the following statement is TRUE?
a)
A quadratic equation in variable x is of the form ax2 + bx + c = 0, where a, b, c are real numbers a ≠ o.
b)
If we can factorise ax2 + bx + c, a ≠ 0 into product of two linear factors then roots can be found by equating each factor to zero
c)
A real number R is said to be a root of the quadratic equation ax2 + bx + c = 0 if a(R)2 + bR + c = 0.
d)
All the above
|
|
Anita Menon answered |
A quadratic equation in variable x is of the form ax2+ bx + c = 0, where a, b, c are real numbers a ≠ o, because if a=0 then the equation becomes a linear equation.
If we can factorise ax2 + bx + c, a ≠ 0 into product of two linear factors then roots can be found by equating each factor to zero because if two factors are in multiplication and equal to zero then either of the factor is zero.
A real number R is said to be a root of the quadratic equation ax2 + bx + c = 0 if a(R)2 + bR + c = 0. , root means that the value gives answer equal to zero.
So all are correct.
If we can factorise ax2 + bx + c, a ≠ 0 into product of two linear factors then roots can be found by equating each factor to zero because if two factors are in multiplication and equal to zero then either of the factor is zero.
A real number R is said to be a root of the quadratic equation ax2 + bx + c = 0 if a(R)2 + bR + c = 0. , root means that the value gives answer equal to zero.
So all are correct.
If -3 is a root of both the Quadratic equations 2x2 + px – 15 = 0, and p(x2 + x) + q = 0, then the value of q if the equation containing it has equal roots is- a)1/2
- b)1/4
- c)14
- d)2
Correct answer is option 'B'. Can you explain this answer?
If -3 is a root of both the Quadratic equations 2x2 + px – 15 = 0, and p(x2 + x) + q = 0, then the value of q if the equation containing it has equal roots is
a)
1/2
b)
1/4
c)
14
d)
2
|
|
Ananya Das answered |
-3 is root of both
2(9) -3p -15 = 0
p = 1
and
second equation has two equal roots so,
b2-4ac = 0
p2 = 4pq
p = 4q
q = 1/4
Which of the following equations has the sum of its roots as 3?
- a)3x2-3x+3 = 0
- b)2x2-3x+6 = 0
- c)-x2+3x-3 = 0
- d)x2+5x+6 = 0
Correct answer is option 'C'. Can you explain this answer?
Which of the following equations has the sum of its roots as 3?
a)
3x2-3x+3 = 0
b)
2x2-3x+6 = 0
c)
-x2+3x-3 = 0
d)
x2+5x+6 = 0
|
|
Anjana Khatri answered |
sum of root = -b/a
for (3) option sum of roots will be -(3)/(-1) = 3
for (3) option sum of roots will be -(3)/(-1) = 3
If x = -2 is a root of equation x2 – 4x + K = 0 then value of K is
- a)8
- b)-8
- c)-12
- d)12
Correct answer is option 'C'. Can you explain this answer?
If x = -2 is a root of equation x2 – 4x + K = 0 then value of K is
a)
8
b)
-8
c)
-12
d)
12
|
|
Mahi Rastogi answered |
(-2)²-4×-2+k=0
4+8+k=0
12+k=0
k=-12} ans
4+8+k=0
12+k=0
k=-12} ans
If x = 1 is a root of equation x2 – Kx + 5 = 0 then value of K is- a)4
- b)6
- c)-6
- d)5
Correct answer is option 'B'. Can you explain this answer?
If x = 1 is a root of equation x2 – Kx + 5 = 0 then value of K is
a)
4
b)
6
c)
-6
d)
5
|
|
Ananya Das answered |
Root of the equation means that the value when substituted in the equation gives zero as answer.
x2 - kx + 5 = 0
Putting x = 1
1*1 -k + 5 = 0
-k+6=0
k=6
x2 - kx + 5 = 0
Putting x = 1
1*1 -k + 5 = 0
-k+6=0
k=6
A real number is said to be a root of ax2+bx+c = 0- a)
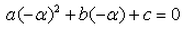
- b)
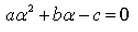
- c)
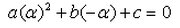
- d)
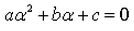
Correct answer is option 'D'. Can you explain this answer?
A real number is said to be a root of ax2+bx+c = 0
a)
b)
c)
d)
|
|
Sameer Diwan answered |
Ni pta re bhai kya likha hai kuch samaj bhi ni aa ra
Zeroes of the quadratic polynomial ax2 + bx + c and roots of the quadratic equation ax2 + bx + c = 0 are ——–- a)Equal to zero
- b)Different
- c)Same
- d)Either same or different
Correct answer is option 'C'. Can you explain this answer?
Zeroes of the quadratic polynomial ax2 + bx + c and roots of the quadratic equation ax2 + bx + c = 0 are ——–
a)
Equal to zero
b)
Different
c)
Same
d)
Either same or different
|
|
Aditi bajaj answered |
Understanding the Relationship Between Zeroes and Roots
The zeroes of a quadratic polynomial and the roots of its corresponding quadratic equation are intrinsically linked concepts in algebra.
Definition of Zeroes and Roots
- The zeroes of a quadratic polynomial ax² + bx + c are the values of x that make the polynomial equal to zero.
- The roots of the quadratic equation ax² + bx + c = 0 are the solutions to this equation.
Key Connection
- Both terms refer to the same values of x where the polynomial intersects the x-axis. Thus, they are essentially the same mathematical entities expressed in different contexts.
Discriminant Analysis
- The nature of the roots (or zeroes) can be determined using the discriminant (D = b² - 4ac):
- If D > 0: Two distinct real roots (zeroes).
- If D = 0: One real root (zero), indicating the roots are equal.
- If D < 0:="" no="" real="" roots="" (zeroes),="" only="" complex="" />
Conclusion
- The statement that the zeroes of the quadratic polynomial and the roots of the quadratic equation are "same" is correct because they represent the same concept.
- Therefore, option 'C' is the appropriate choice, as both zeroes and roots indicate the values where the polynomial equals zero.
In summary, understanding that the zeroes of a polynomial and the roots of its equation are synonymous is crucial for grasping the fundamentals of quadratic functions.
The zeroes of a quadratic polynomial and the roots of its corresponding quadratic equation are intrinsically linked concepts in algebra.
Definition of Zeroes and Roots
- The zeroes of a quadratic polynomial ax² + bx + c are the values of x that make the polynomial equal to zero.
- The roots of the quadratic equation ax² + bx + c = 0 are the solutions to this equation.
Key Connection
- Both terms refer to the same values of x where the polynomial intersects the x-axis. Thus, they are essentially the same mathematical entities expressed in different contexts.
Discriminant Analysis
- The nature of the roots (or zeroes) can be determined using the discriminant (D = b² - 4ac):
- If D > 0: Two distinct real roots (zeroes).
- If D = 0: One real root (zero), indicating the roots are equal.
- If D < 0:="" no="" real="" roots="" (zeroes),="" only="" complex="" />
Conclusion
- The statement that the zeroes of the quadratic polynomial and the roots of the quadratic equation are "same" is correct because they represent the same concept.
- Therefore, option 'C' is the appropriate choice, as both zeroes and roots indicate the values where the polynomial equals zero.
In summary, understanding that the zeroes of a polynomial and the roots of its equation are synonymous is crucial for grasping the fundamentals of quadratic functions.
Multiplication of ‘ab’ and ‘a-b’ is- a)a2b-b
- b)a2b+b
- c)ba2b+ab2
- d)a2b - ab2
Correct answer is option 'D'. Can you explain this answer?
Multiplication of ‘ab’ and ‘a-b’ is
a)
a2b-b
b)
a2b+b
c)
ba2b+ab2
d)
a2b - ab2
|
Akhilesh Rajput answered |
Answer d is correct
(ab) ( a- b)
= a^2 b - ab^2 ok
(ab) ( a- b)
= a^2 b - ab^2 ok
Chapter doubts & questions for Algebra - Mathematics for BMAT (Section 2) 2025 is part of BMAT exam preparation. The chapters have been prepared according to the BMAT exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for BMAT 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Algebra - Mathematics for BMAT (Section 2) in English & Hindi are available as part of BMAT exam.
Download more important topics, notes, lectures and mock test series for BMAT Exam by signing up for free.
Mathematics for BMAT (Section 2)
52 videos|41 docs|34 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily