All Exams >
GMAT >
Data Insights for GMAT >
All Questions
All questions of Mock Test: Data Sufficiency for GMAT Exam
a < b. Is a positive?
1. b = 0.
2. √a < a
- a)EACH statement ALONE is sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question ask
- d)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'A'. Can you explain this answer?
a < b. Is a positive?
1. b = 0.
2. √a < a
1. b = 0.
2. √a < a
a)
EACH statement ALONE is sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question ask
d)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.

|
Shivam Ghoshal answered |
In statement 1, b =0, when a < b and b = 0, it implies that a < 0, hence, a is negative and a is not positive. The statement is sufficient.
In statement 2, √a < a, the square root of a number is defined only when in √a a > 0 . Hence, the statement is sufficient. Thus, EACH statement ALONE is sufficient to answer the question asked.
In statement 2, √a < a, the square root of a number is defined only when in √a a > 0 . Hence, the statement is sufficient. Thus, EACH statement ALONE is sufficient to answer the question asked.
Determine the size of an interior angle of the polygon.
1. The ratio of its interior angle to the exterior angle is 2:1.
2. The polygon is a regular hexagon
- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)EACH statement ALONE is sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question ask
- d)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'B'. Can you explain this answer?
Determine the size of an interior angle of the polygon.
1. The ratio of its interior angle to the exterior angle is 2:1.
2. The polygon is a regular hexagon
1. The ratio of its interior angle to the exterior angle is 2:1.
2. The polygon is a regular hexagon
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
EACH statement ALONE is sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question ask
d)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.

|
Hridoy Gupta answered |


Conclusion:
Since both statements independently lead to the determination that the interior angle is 120 degrees, each statement alone is sufficient.
The correct answer is:
EACH statement ALONE is sufficient to answer the question asked.
The area of a triangle is equal to the area of the rectangle. Find the perimeter of the rectangle.
1. The perimeter of the square is 24 inches.
2. The sum of the length and the width is 13 inches.
- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question.
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'C'. Can you explain this answer?
The area of a triangle is equal to the area of the rectangle. Find the perimeter of the rectangle.
1. The perimeter of the square is 24 inches.
2. The sum of the length and the width is 13 inches.
1. The perimeter of the square is 24 inches.
2. The sum of the length and the width is 13 inches.
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question.
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.

|
Anirban Das answered |
Explanation:
Let the sides of the square be s, and the length and width of the rectangle be l and w, respectively. We need to find the perimeter of the rectangle, which is 2(l+w).
Statement 1: The perimeter of the square is 24 inches.
This means that s=6 inches. Since the area of the triangle is equal to the area of the rectangle, we have (1/2)(s^2) = lw. So, (1/2)(6^2) = lw, which means lw=18. However, we cannot determine l and w from this statement alone, so it is not sufficient.
Statement 2: The sum of the length and the width is 13 inches.
This means that l+w=13. We cannot determine the area or the perimeter of the rectangle from this statement alone, so it is not sufficient.
Using both statements together, we know that lw=18 and l+w=13. We can solve for l and w using these equations: l=9 and w=4 (or vice versa). Now we can find the perimeter of the rectangle: 2(9+4) = 26 inches. Both statements together are sufficient to answer the question.
Let the sides of the square be s, and the length and width of the rectangle be l and w, respectively. We need to find the perimeter of the rectangle, which is 2(l+w).
Statement 1: The perimeter of the square is 24 inches.
This means that s=6 inches. Since the area of the triangle is equal to the area of the rectangle, we have (1/2)(s^2) = lw. So, (1/2)(6^2) = lw, which means lw=18. However, we cannot determine l and w from this statement alone, so it is not sufficient.
Statement 2: The sum of the length and the width is 13 inches.
This means that l+w=13. We cannot determine the area or the perimeter of the rectangle from this statement alone, so it is not sufficient.
Using both statements together, we know that lw=18 and l+w=13. We can solve for l and w using these equations: l=9 and w=4 (or vice versa). Now we can find the perimeter of the rectangle: 2(9+4) = 26 inches. Both statements together are sufficient to answer the question.
Two numbers 12 and t are two positive numbers with some similar properties. What is the value of t.
1. The Least Common Multiple of the two numbers 48.
2. The Greatest Common divisor of the two numbers is 4.
- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question ask
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'C'. Can you explain this answer?
Two numbers 12 and t are two positive numbers with some similar properties. What is the value of t.
1. The Least Common Multiple of the two numbers 48.
2. The Greatest Common divisor of the two numbers is 4.
1. The Least Common Multiple of the two numbers 48.
2. The Greatest Common divisor of the two numbers is 4.
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question ask
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.

|
Shivam Ghoshal answered |
We consider 12 and t.
In statement 1, the Least Common multiple of 12 and t is 48 to mean that t is a factor of 48. This mean that, t can take 16, 24 and 48. Hence the statement is not sufficient.
In statement 2, the Greatest Common divisor is 4. Therefore, t can take 4, 8, 16, 28, 32, 40 among others. Thus, the statement is not sufficient.
Combining statements 1and 2, we have 16 featuring in both lists, hence it satisfies the two conditions. Therefore, t =16. Thus BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
In statement 1, the Least Common multiple of 12 and t is 48 to mean that t is a factor of 48. This mean that, t can take 16, 24 and 48. Hence the statement is not sufficient.
In statement 2, the Greatest Common divisor is 4. Therefore, t can take 4, 8, 16, 28, 32, 40 among others. Thus, the statement is not sufficient.
Combining statements 1and 2, we have 16 featuring in both lists, hence it satisfies the two conditions. Therefore, t =16. Thus BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
If x and y are distinct positive integers, what is the value of x4-y4?
1)(y2+ x2)(y + x)(x -y) = 240
2)xy= yx and x > y- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
- c)BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
- d)EACH statement ALONE is sufficient.
- e)Statement (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data are needed.
Correct answer is option 'D'. Can you explain this answer?
If x and y are distinct positive integers, what is the value of x4-y4?
1)(y2+ x2)(y + x)(x -y) = 240
2)xy= yx and x > y
1)(y2+ x2)(y + x)(x -y) = 240
2)xy= yx and x > y
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
c)
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
d)
EACH statement ALONE is sufficient.
e)
Statement (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data are needed.

|
Kiran Chauhan answered |
Before even evaluating the statements, simplify the question. In a more complicated data sufficiency problem, it is likely that some rearranging of the terms will be necessary in order to see the correct answer.
Use the formula for a difference of squares (a2 - b2) = (a + b)(a - b). However, let x2 equal a, meaning a2 = x4.
x4 - y4 = (x2 + y2)(x2 - y2)
Recognize that the expression contains another difference of squares and can be simplified even further.
(x2 + y2)(x2 – y2) = (x2 + y2)(x – y)(x + y)
The question can now be simplified to: "If x and y are distinct positive integers, what is the value of (x2 + y2)(x – y)(x + y)?" If you can find the value of (x2 + y2)(x - y)(x + y) or x4 - y4, you have sufficient data.
Evaluate Statement (1) alone.
Statement (1) says (y2 + x2)(y + x)(x - y) = 240. The information in Statement (1) matches exactly the simplified question. Statement (1) is SUFFICIENT.
Evaluate Statement (2) alone.
Statement (2) says xy = yx and x > y. In other words, the product of multiplying x together y times equals the product of multiplying y together x times.
The differences in the bases must compensate for the fact that y is being multiplied more times than x (since x > y and y is being multiplied x times while x is being multiplied y times).
4 and 2 are the only numbers that work because only 4 and 2 satisfy the equation n2 = 2n, which is the condition that would be necessary for the equation to hold true.
Observe that this is true: 42 = 24 = 16.
Remember that x > y, so x = 4 and y = 2. Consequently, you know the value of x4 - y4 from Statement (2). So, Statement (2) is SUFFICIENT.
Since Statement (1) alone is SUFFICIENT and Statement (2) alone is SUFFICIENT
Use the formula for a difference of squares (a2 - b2) = (a + b)(a - b). However, let x2 equal a, meaning a2 = x4.
x4 - y4 = (x2 + y2)(x2 - y2)
Recognize that the expression contains another difference of squares and can be simplified even further.
(x2 + y2)(x2 – y2) = (x2 + y2)(x – y)(x + y)
The question can now be simplified to: "If x and y are distinct positive integers, what is the value of (x2 + y2)(x – y)(x + y)?" If you can find the value of (x2 + y2)(x - y)(x + y) or x4 - y4, you have sufficient data.
Evaluate Statement (1) alone.
Statement (1) says (y2 + x2)(y + x)(x - y) = 240. The information in Statement (1) matches exactly the simplified question. Statement (1) is SUFFICIENT.
Evaluate Statement (2) alone.
Statement (2) says xy = yx and x > y. In other words, the product of multiplying x together y times equals the product of multiplying y together x times.
The differences in the bases must compensate for the fact that y is being multiplied more times than x (since x > y and y is being multiplied x times while x is being multiplied y times).
4 and 2 are the only numbers that work because only 4 and 2 satisfy the equation n2 = 2n, which is the condition that would be necessary for the equation to hold true.
Observe that this is true: 42 = 24 = 16.
Remember that x > y, so x = 4 and y = 2. Consequently, you know the value of x4 - y4 from Statement (2). So, Statement (2) is SUFFICIENT.
Since Statement (1) alone is SUFFICIENT and Statement (2) alone is SUFFICIENT
Determine the equation of the circle passing through (-4,-2).
1. (1,-1) lies in the circle.
2. The center of the circle is the origin.- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question ask
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'B'. Can you explain this answer?
Determine the equation of the circle passing through (-4,-2).
1. (1,-1) lies in the circle.
2. The center of the circle is the origin.
1. (1,-1) lies in the circle.
2. The center of the circle is the origin.
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question ask
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.

|
Avantika Sengupta answered |
Statement (2) alone is sufficient to answer the question asked.
Explanation:
For a circle passing through (-4,-2) and with the center at the origin, the equation of the circle can be written as:
(x - 0)^2 + (y - 0)^2 = r^2
where r is the radius of the circle.
Now, let's consider statement (1):
(1,-1) lies in the circle.
If we substitute this point in the equation of the circle, we get:
(1 - 0)^2 + (-1 - 0)^2 = r^2
which simplifies to:
2 = r^2
So, we know the value of r, but we still don't have the equation of the circle.
On the other hand, statement (2) tells us that the center of the circle is at the origin. This means that we can write the equation of the circle as:
x^2 + y^2 = r^2
where r is the radius of the circle that we found in statement (1).
Therefore, statement (2) alone is sufficient to answer the question asked, and the correct answer is option (B).
Explanation:
For a circle passing through (-4,-2) and with the center at the origin, the equation of the circle can be written as:
(x - 0)^2 + (y - 0)^2 = r^2
where r is the radius of the circle.
Now, let's consider statement (1):
(1,-1) lies in the circle.
If we substitute this point in the equation of the circle, we get:
(1 - 0)^2 + (-1 - 0)^2 = r^2
which simplifies to:
2 = r^2
So, we know the value of r, but we still don't have the equation of the circle.
On the other hand, statement (2) tells us that the center of the circle is at the origin. This means that we can write the equation of the circle as:
x^2 + y^2 = r^2
where r is the radius of the circle that we found in statement (1).
Therefore, statement (2) alone is sufficient to answer the question asked, and the correct answer is option (B).
Find out if t < 0.
1. |t| > t
2. t2 > 0- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question ask
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'A'. Can you explain this answer?
Find out if t < 0.
1. |t| > t
2. t2 > 0
1. |t| > t
2. t2 > 0
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question ask
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.

|
Shivam Ghoshal answered |
In statement 1, |t| > t. But is |-t| = |t|. Hence t can be positive or negative. When |t| > t, it implies that t is a negative value, hence t < 0. The statement is sufficient.
In statement 2, t2 > 0 , but when t is negative or positive, t2 > 0 , hence the statement is not sufficient. Thus Statement (1) ALONE is sufficient but statement (2) is not sufficient.
In statement 2, t2 > 0 , but when t is negative or positive, t2 > 0 , hence the statement is not sufficient. Thus Statement (1) ALONE is sufficient but statement (2) is not sufficient.
Find the percentage change in the volume of cylinder.
1. The diameter is increased by 20%.
2. The height is increased by 21%.- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question ask
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'D'. Can you explain this answer?
Find the percentage change in the volume of cylinder.
1. The diameter is increased by 20%.
2. The height is increased by 21%.
1. The diameter is increased by 20%.
2. The height is increased by 21%.
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question ask
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.

|
Shivam Ghoshal answered |
The volume of the cylinder is given buy v = πr²h.
In statement 1, diameter (d) is increased by 20%, hence the radius is increased by 10%. The new radius is given by 1.1r. The new volume = π(1.1r)²h = 1.21πr²h
Percentage change in volume = (1.21πr²h - πr²h )/pr²h × 100% = 21%. The statement is sufficient.
In statement 2, height is increased by 21%, hence the new height is 1.21h. The new volume = 1.21πr²h.
Percentage change in volume = (1.21πr²h - πr²h )/πr²h × 100% = 21%. The statement is sufficient. Therefore, EACH statement ALONE is sufficient.
In statement 1, diameter (d) is increased by 20%, hence the radius is increased by 10%. The new radius is given by 1.1r. The new volume = π(1.1r)²h = 1.21πr²h
Percentage change in volume = (1.21πr²h - πr²h )/pr²h × 100% = 21%. The statement is sufficient.
In statement 2, height is increased by 21%, hence the new height is 1.21h. The new volume = 1.21πr²h.
Percentage change in volume = (1.21πr²h - πr²h )/πr²h × 100% = 21%. The statement is sufficient. Therefore, EACH statement ALONE is sufficient.
x is a positive integer; what is the value of x?
1)The sum of any two positive factors of x is even
2)x is a prime number and x < 4- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
- c)BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
- d)EACH statement ALONE is sufficient.
- e)Statement (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data are needed.
Correct answer is option 'C'. Can you explain this answer?
x is a positive integer; what is the value of x?
1)The sum of any two positive factors of x is even
2)x is a prime number and x < 4
1)The sum of any two positive factors of x is even
2)x is a prime number and x < 4
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
c)
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
d)
EACH statement ALONE is sufficient.
e)
Statement (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data are needed.

|
Chirag Roy answered |
Understanding the Problem
We need to determine the value of x, a positive integer, based on two statements.
Statement 1: The sum of any two positive factors of x is even
- Factors of x: Positive factors of any number include 1, itself, and other divisors.
- Even Sum: The sum of two factors is even if both factors are odd or both are even.
- Conclusion: If x has only even factors, x must be even. If x has odd factors, then x must be odd. The only case where all factors are odd is for x=1 (which isn't useful as it's not considered in the context of even factors). So, this statement suggests x could only be 2, an even prime number.
Statement 2: x is a prime number and x < />
- Possible Values of x: The prime numbers less than 4 are 2 and 3.
- Conclusion: This statement gives us two possible values for x (2 or 3).
Combining Statements 1 and 2
- From Statement 1: x must be 2 since the sum of any two factors (1 and 2) is 3 (odd), but 2 is the only even prime.
- From Statement 2: x could be 2 or 3. However, since x must be even (from Statement 1), the only valid value is 2.
Final Conclusion
- Both statements together confirm that x must equal 2.
- Hence, both statements are necessary for arriving at the unique solution.
Thus, the correct answer is option 'C': BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
We need to determine the value of x, a positive integer, based on two statements.
Statement 1: The sum of any two positive factors of x is even
- Factors of x: Positive factors of any number include 1, itself, and other divisors.
- Even Sum: The sum of two factors is even if both factors are odd or both are even.
- Conclusion: If x has only even factors, x must be even. If x has odd factors, then x must be odd. The only case where all factors are odd is for x=1 (which isn't useful as it's not considered in the context of even factors). So, this statement suggests x could only be 2, an even prime number.
Statement 2: x is a prime number and x < />
- Possible Values of x: The prime numbers less than 4 are 2 and 3.
- Conclusion: This statement gives us two possible values for x (2 or 3).
Combining Statements 1 and 2
- From Statement 1: x must be 2 since the sum of any two factors (1 and 2) is 3 (odd), but 2 is the only even prime.
- From Statement 2: x could be 2 or 3. However, since x must be even (from Statement 1), the only valid value is 2.
Final Conclusion
- Both statements together confirm that x must equal 2.
- Hence, both statements are necessary for arriving at the unique solution.
Thus, the correct answer is option 'C': BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
Consider a set S = {2, 4, 6, 8, x, y} with distinct elements. If x and y are both prime numbers and 0 < x < 40 and 0 < y < 40, which of the following MUST be true?
I. The maximum possible range of the set is greater than 33.
II. The median can never be an even number.
III. If y = 37, the average of the set will be greater than the median.- a)I only
- b)I and II only
- c)I, II, and III
- d)III only
Correct answer is option 'C'. Can you explain this answer?
Consider a set S = {2, 4, 6, 8, x, y} with distinct elements. If x and y are both prime numbers and 0 < x < 40 and 0 < y < 40, which of the following MUST be true?
I. The maximum possible range of the set is greater than 33.
II. The median can never be an even number.
III. If y = 37, the average of the set will be greater than the median.
I. The maximum possible range of the set is greater than 33.
II. The median can never be an even number.
III. If y = 37, the average of the set will be greater than the median.
a)
I only
b)
I and II only
c)
I, II, and III
d)
III only

|
EduRev GMAT answered |
Step 1: Key Data from the Question
Set S has 6 elements.
The elements of set S are distinct.
x and y are prime numbers. Because 2 is already an element in S, both x and y have to be odd.
0 < x < 40 and 0 < y < 40
The elements of set S are distinct.
x and y are prime numbers. Because 2 is already an element in S, both x and y have to be odd.
0 < x < 40 and 0 < y < 40
Step 2: Check Statement I
I. The maximum possible range of the set is greater than 33.
The keyword in this entire statement is maximum. We have to determine whether the maximum value possible for the range exceeds 33.
We know x and y are prime numbers. The largest prime number less than 40 is 37.
If either x or y is 37, the largest number in the set will be 37 and the smallest number is 2.
Therefore, the maximum range of the set will be 37 - 2 = 35. It is greater than 33.
The keyword in this entire statement is maximum. We have to determine whether the maximum value possible for the range exceeds 33.
We know x and y are prime numbers. The largest prime number less than 40 is 37.
If either x or y is 37, the largest number in the set will be 37 and the smallest number is 2.
Therefore, the maximum range of the set will be 37 - 2 = 35. It is greater than 33.
Statement I is true. So, eliminate choices that do not contain I.
Eliminate choice D
Eliminate choice D
Step 3: Check Statement II
II. The median can never be an even number.
There are 6 numbers in the set. Therefore, the median is the arithmetic mean of the 3rd and the 4th term when the numbers are written in ascending or descending order.
The elements are {2, 4, 6, 8, x, y}, where x and y are prime numbers.
If x and y take 3 and 5 as values, the median is 4.5
If x = 3, y = 7 or greater, the median is 5.
If x = 5, y = 7 or greater, the median is 5.5
If x = 7, y = 11 or greater, the median is 6.5
If x = 11 or greater and y = 13 or greater, the median is 7.
It is quite clear that the median is either an odd number or is not an interger. So, the median can never be an even integer.
There are 6 numbers in the set. Therefore, the median is the arithmetic mean of the 3rd and the 4th term when the numbers are written in ascending or descending order.
The elements are {2, 4, 6, 8, x, y}, where x and y are prime numbers.
If x and y take 3 and 5 as values, the median is 4.5
If x = 3, y = 7 or greater, the median is 5.
If x = 5, y = 7 or greater, the median is 5.5
If x = 7, y = 11 or greater, the median is 6.5
If x = 11 or greater and y = 13 or greater, the median is 7.
It is quite clear that the median is either an odd number or is not an interger. So, the median can never be an even integer.
Statement II is true. Eliminate choices that do not contain II.
Eliminate choices A and C as well.
Eliminate choices A and C as well.
Step 4: Check Statement III
III. If y = 37, the average of the set will be greater than the median.
If y = 37, the set will be {2, 4, 6, 8, x, 37}, where x is a prime number greater than 2 and less than 37.
The average will be 57 + x657 + x6 = 9.5 + x6x6
If x = 3, median = 5 and average = 10. Average > median.
If x = 5, median = 5.5 and average = 10.33. Average > median
If x = 7, median = 6.5 and average = 10.66. Average > medain
If x = 11 or greater, the median = 7. Average will be definitely greater than 10. So, Average > Median.
It is true that the average is greater than the median if y = 37.
If y = 37, the set will be {2, 4, 6, 8, x, 37}, where x is a prime number greater than 2 and less than 37.
The average will be 57 + x657 + x6 = 9.5 + x6x6
If x = 3, median = 5 and average = 10. Average > median.
If x = 5, median = 5.5 and average = 10.33. Average > median
If x = 7, median = 6.5 and average = 10.66. Average > medain
If x = 11 or greater, the median = 7. Average will be definitely greater than 10. So, Average > Median.
It is true that the average is greater than the median if y = 37.
Statement III is also true.
Statements I, II, and III are true.
Statements I, II, and III are true.
Choice C is the correct answer.
Determine the value of angle k.
1. Angle k and m lies on a straight line.
2. Angle m = 39° .- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question ask
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'C'. Can you explain this answer?
Determine the value of angle k.
1. Angle k and m lies on a straight line.
2. Angle m = 39° .
1. Angle k and m lies on a straight line.
2. Angle m = 39° .
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question ask
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.

|
Navya Yadav answered |
Unfortunately, without additional information, we cannot determine the value of angle k.
Is A an obtuse angle?
1. A is more than 90°.
2. A is a supplement of an angle B, an acute triangle.- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question ask
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'B'. Can you explain this answer?
Is A an obtuse angle?
1. A is more than 90°.
2. A is a supplement of an angle B, an acute triangle.
1. A is more than 90°.
2. A is a supplement of an angle B, an acute triangle.
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question ask
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.

|
Aditya Gupta answered |
Yes, if A is more than 90 degrees, it is an obtuse angle.
Ann deposited $3000 in her bank account at the beginning of the year. Determine the amount the funds accumulated to.
1. The bank offered 4.3% interest rate.
2. The amount was deposited for a period of 5 years.- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question ask
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'E'. Can you explain this answer?
Ann deposited $3000 in her bank account at the beginning of the year. Determine the amount the funds accumulated to.
1. The bank offered 4.3% interest rate.
2. The amount was deposited for a period of 5 years.
1. The bank offered 4.3% interest rate.
2. The amount was deposited for a period of 5 years.
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question ask
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.

|
Prisha Mukherjee answered |
Deposit (P) = 3000.
Accumulated amount = P + (1 + R/100)n where the variables have their usual meaning for compound interest and
Accumulated amount = P + (P × r/100 × n) where the variables have their usual meaning for simple interest.
In statement 1, r = 4.3 and P = 3000 but we are not given the value of n, hence we cannot find the accumulated amount. Further more, the statement does not give more information about the kind of interest offered, hence, it is not sufficient.
In statement 2, n = 5 and P = 3000 but we are not given the value of r, hence we cannot find the accumulated amount. Furthermore, the statement does not give more information about the kind of interest offered, hence, it is not sufficient.
Combining the two statements, P = 3000, r = 4.5 and n = 5 but, the details given are not sufficient since no specific type on interest is disclosed, therefore, we cannot apply the compound or simple interest formula with accuracy. Thus Statements (1) and (2) TOGETHER are NOT sufficient.
Accumulated amount = P + (1 + R/100)n where the variables have their usual meaning for compound interest and
Accumulated amount = P + (P × r/100 × n) where the variables have their usual meaning for simple interest.
In statement 1, r = 4.3 and P = 3000 but we are not given the value of n, hence we cannot find the accumulated amount. Further more, the statement does not give more information about the kind of interest offered, hence, it is not sufficient.
In statement 2, n = 5 and P = 3000 but we are not given the value of r, hence we cannot find the accumulated amount. Furthermore, the statement does not give more information about the kind of interest offered, hence, it is not sufficient.
Combining the two statements, P = 3000, r = 4.5 and n = 5 but, the details given are not sufficient since no specific type on interest is disclosed, therefore, we cannot apply the compound or simple interest formula with accuracy. Thus Statements (1) and (2) TOGETHER are NOT sufficient.
Are the two lines L1 and L2 parallel?
1. Both lines lie in the first, second and fourth quadrants.
2. The y intercepts of the lines L1 and L2 are 8 and 4 respectively.- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question ask
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'E'. Can you explain this answer?
Are the two lines L1 and L2 parallel?
1. Both lines lie in the first, second and fourth quadrants.
2. The y intercepts of the lines L1 and L2 are 8 and 4 respectively.
1. Both lines lie in the first, second and fourth quadrants.
2. The y intercepts of the lines L1 and L2 are 8 and 4 respectively.
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question ask
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.

|
Shivam Ghoshal answered |
Parallel lines have equal slopes.
In statement 1, if both lines are in the first, second and fourth quadrant then they have a negative slope. This alone is not enough to prove that they are parallel or not, hence, the statement is insufficient.
In statement 2, the y intercepts are 8 and 4 to imply that the equation are of the form y = mx + 8 and y = bx + 4. But this does not enough to determine if the lines area parallel since, notheing is said about the value of m and b, hence, the statement too is insufficient.
Combining the two statements, we have equations having negative gradients, thus, y =-mx + 8 and y = -bx + 4. Since we are not sure of -m = -b, we cannot say that they are parallel on not. Therefore, Statements (1) and (2) TOGETHER are NOT sufficient.
In statement 1, if both lines are in the first, second and fourth quadrant then they have a negative slope. This alone is not enough to prove that they are parallel or not, hence, the statement is insufficient.
In statement 2, the y intercepts are 8 and 4 to imply that the equation are of the form y = mx + 8 and y = bx + 4. But this does not enough to determine if the lines area parallel since, notheing is said about the value of m and b, hence, the statement too is insufficient.
Combining the two statements, we have equations having negative gradients, thus, y =-mx + 8 and y = -bx + 4. Since we are not sure of -m = -b, we cannot say that they are parallel on not. Therefore, Statements (1) and (2) TOGETHER are NOT sufficient.
Two pipes supply waters to a cistern whose capacity of 15 cubic feet. How long does it take the two pipes to fill the cistern?
1. The first pipe supplies water at a rate (per minute) that is thrice faster than the second pipe.
2. The pipes fill 8 cubic feet of the tank in ten minute.- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question ask
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'B'. Can you explain this answer?
Two pipes supply waters to a cistern whose capacity of 15 cubic feet. How long does it take the two pipes to fill the cistern?
1. The first pipe supplies water at a rate (per minute) that is thrice faster than the second pipe.
2. The pipes fill 8 cubic feet of the tank in ten minute.
1. The first pipe supplies water at a rate (per minute) that is thrice faster than the second pipe.
2. The pipes fill 8 cubic feet of the tank in ten minute.
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question ask
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.

|
Sankar Desai answered |
Statement 1:
The first pipe supplies water at a rate (per minute) that is thrice faster than the second pipe.
This statement provides information about the relative rates of the two pipes. Let's assume that the second pipe fills the cistern in 'x' minutes. Therefore, the first pipe, which is thrice as fast, will fill the cistern in 'x/3' minutes.
Statement 2:
The pipes fill 8 cubic feet of the tank in ten minutes.
This statement provides information about the combined rate of both pipes. In ten minutes, the pipes fill 8 cubic feet of the tank.
Combined analysis:
From statement 1, we know that the first pipe fills the cistern in 'x/3' minutes, and the second pipe fills it in 'x' minutes.
In one minute, the combined rate of both pipes is (1/x + 1/(x/3)) = (1/x + 3/x) = 4/x.
From statement 2, we know that in ten minutes, the pipes fill 8 cubic feet of the tank.
Therefore, in one minute, the combined rate of both pipes is 8/10 = 4/5.
Now we have two equations:
4/x = 4/5
x = 5
Conclusion:
We can determine that it takes the second pipe 5 minutes to fill the cistern on its own. Therefore, statement 2 alone is sufficient to answer the question, but statement 1 alone is not. Hence, the correct answer is option B.
The first pipe supplies water at a rate (per minute) that is thrice faster than the second pipe.
This statement provides information about the relative rates of the two pipes. Let's assume that the second pipe fills the cistern in 'x' minutes. Therefore, the first pipe, which is thrice as fast, will fill the cistern in 'x/3' minutes.
Statement 2:
The pipes fill 8 cubic feet of the tank in ten minutes.
This statement provides information about the combined rate of both pipes. In ten minutes, the pipes fill 8 cubic feet of the tank.
Combined analysis:
From statement 1, we know that the first pipe fills the cistern in 'x/3' minutes, and the second pipe fills it in 'x' minutes.
In one minute, the combined rate of both pipes is (1/x + 1/(x/3)) = (1/x + 3/x) = 4/x.
From statement 2, we know that in ten minutes, the pipes fill 8 cubic feet of the tank.
Therefore, in one minute, the combined rate of both pipes is 8/10 = 4/5.
Now we have two equations:
4/x = 4/5
x = 5
Conclusion:
We can determine that it takes the second pipe 5 minutes to fill the cistern on its own. Therefore, statement 2 alone is sufficient to answer the question, but statement 1 alone is not. Hence, the correct answer is option B.
Determine the area of a triangle A.
1. Triangle A and B are similar with a linear scale factor of 7 : 10.
2. B is larger than A.- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question ask
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'E'. Can you explain this answer?
Determine the area of a triangle A.
1. Triangle A and B are similar with a linear scale factor of 7 : 10.
2. B is larger than A.
1. Triangle A and B are similar with a linear scale factor of 7 : 10.
2. B is larger than A.
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question ask
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.

|
Nilotpal Sen answered |
Statement 1: Triangle A and B are similar with a linear scale factor of 7:10.
Statement 2: B is larger than A.
To determine the area of triangle A, we need to know the specific measurements of the triangle. However, neither statement alone provides us with enough information to calculate the area of triangle A. Let's analyze each statement separately.
Statement 1: Triangle A and B are similar with a linear scale factor of 7:10.
This statement tells us that the ratio of corresponding sides of triangles A and B is 7:10. However, it doesn't provide us with any information about the specific lengths of the sides or the height of triangle A. Therefore, we cannot determine the area of triangle A based on this statement alone.
Statement 2: B is larger than A.
This statement tells us that triangle B is larger than triangle A, but it doesn't provide any information about the specific measurements of either triangle. Without knowing the measurements of triangle A, we cannot calculate its area based on this statement alone.
Both Statements Together:
When we consider both statements together, we still don't have enough information to calculate the area of triangle A. While statement 1 tells us about the similarity between the triangles, it doesn't provide any specific measurements. And statement 2 only tells us that triangle B is larger than A, but it doesn't give us any measurements either.
Therefore, the correct answer is option E: Statements (1) and (2) together are not sufficient to answer the question asked, and additional data specific to the problem are needed.
Statement 2: B is larger than A.
To determine the area of triangle A, we need to know the specific measurements of the triangle. However, neither statement alone provides us with enough information to calculate the area of triangle A. Let's analyze each statement separately.
Statement 1: Triangle A and B are similar with a linear scale factor of 7:10.
This statement tells us that the ratio of corresponding sides of triangles A and B is 7:10. However, it doesn't provide us with any information about the specific lengths of the sides or the height of triangle A. Therefore, we cannot determine the area of triangle A based on this statement alone.
Statement 2: B is larger than A.
This statement tells us that triangle B is larger than triangle A, but it doesn't provide any information about the specific measurements of either triangle. Without knowing the measurements of triangle A, we cannot calculate its area based on this statement alone.
Both Statements Together:
When we consider both statements together, we still don't have enough information to calculate the area of triangle A. While statement 1 tells us about the similarity between the triangles, it doesn't provide any specific measurements. And statement 2 only tells us that triangle B is larger than A, but it doesn't give us any measurements either.
Therefore, the correct answer is option E: Statements (1) and (2) together are not sufficient to answer the question asked, and additional data specific to the problem are needed.
After a long career, John C. Walden is retiring. If there are 25 associates who contribute equally to a parting gift for John in an amount that is an integer, what is the total value of the parting gift?
1) If four associates were fired for underperformance, the total value of the parting gift would have decreased by $200
2) The value of the parting gift is greater than $1,225 and less than $1,275- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
- c)BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
- d)EACH statement ALONE is sufficient.
- e)Statement (1) and (2) TOGETHER are NOT sufficient to answer the question asked, andadditional data are needed.
Correct answer is option 'D'. Can you explain this answer?
After a long career, John C. Walden is retiring. If there are 25 associates who contribute equally to a parting gift for John in an amount that is an integer, what is the total value of the parting gift?
1) If four associates were fired for underperformance, the total value of the parting gift would have decreased by $200
2) The value of the parting gift is greater than $1,225 and less than $1,275
1) If four associates were fired for underperformance, the total value of the parting gift would have decreased by $200
2) The value of the parting gift is greater than $1,225 and less than $1,275
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
c)
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
d)
EACH statement ALONE is sufficient.
e)
Statement (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and
additional data are needed.

|
Arnab Kumar answered |
Simplify the question by translating it into algebra.
Let P = the total value of John's parting gift
Let E = the amount each associate contributed
Let N = the number of associates
P = NE = 25E
With this algebraic equation, if you find the value of either P or E, you will know the total value of the parting gift.
Evaluate Statement (1) alone.
Two common ways to evaluate Statement (1) alone:
Statement 1: Method 1
Since the question stated that each person contributed equally, if losing four associates decreased the total value of the parting gift by $200, then the value of each associate's contribution was $50 (=$200/4).
Consequently, P = 25E = 25(50) = $1,250.
Statement 1: Method 2
If four associates leave, there are N - 4 = 25 - 4 = 21 associates.
If the value of the parting gift decreases by $200, its new value will be P - 200.
Taken together, Statement (1) can be translated:
P - 200 = 21E
P = 21E + 200
You now have two unique equations and two variables, which means that Statement (1) is SUFFICIENT.
Although you should not spend time finding the solution on the test, here is the solution.
Equation 1: P = 21E + 200
Equation 2: P = 25E
P = P
25E = 21E + 200
4E = 200
E = $50
P = NE = 25E = 25($50) = $1250
Evaluate Statement (2) alone.
Statement (2) says that $1,225 < P < $1,275. It is crucial to remember that the question stated that "25 associates contribute equally to a parting gift for John in an amount that is an integer." In other words P / 25 must be an integer. Stated differently, P must be a multiple of 25.
There is only one multiple of 25 between 1,225 and 1,275. That number is $1,250. Since there is only one possible value for P, Statement (2) is SUFFICIENT.
Since Statement (1) alone is SUFFICIENT and Statement (2) alone is SUFFICIENT, answer D is correct.
Let P = the total value of John's parting gift
Let E = the amount each associate contributed
Let N = the number of associates
P = NE = 25E
With this algebraic equation, if you find the value of either P or E, you will know the total value of the parting gift.
Evaluate Statement (1) alone.
Two common ways to evaluate Statement (1) alone:
Statement 1: Method 1
Since the question stated that each person contributed equally, if losing four associates decreased the total value of the parting gift by $200, then the value of each associate's contribution was $50 (=$200/4).
Consequently, P = 25E = 25(50) = $1,250.
Statement 1: Method 2
If four associates leave, there are N - 4 = 25 - 4 = 21 associates.
If the value of the parting gift decreases by $200, its new value will be P - 200.
Taken together, Statement (1) can be translated:
P - 200 = 21E
P = 21E + 200
You now have two unique equations and two variables, which means that Statement (1) is SUFFICIENT.
Although you should not spend time finding the solution on the test, here is the solution.
Equation 1: P = 21E + 200
Equation 2: P = 25E
P = P
25E = 21E + 200
4E = 200
E = $50
P = NE = 25E = 25($50) = $1250
Evaluate Statement (2) alone.
Statement (2) says that $1,225 < P < $1,275. It is crucial to remember that the question stated that "25 associates contribute equally to a parting gift for John in an amount that is an integer." In other words P / 25 must be an integer. Stated differently, P must be a multiple of 25.
There is only one multiple of 25 between 1,225 and 1,275. That number is $1,250. Since there is only one possible value for P, Statement (2) is SUFFICIENT.
Since Statement (1) alone is SUFFICIENT and Statement (2) alone is SUFFICIENT, answer D is correct.
Find the equation of a line.
1. Its x and y intercept is 2 and -2 respectively.
2. The slope of the line is 1.- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question ask
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'A'. Can you explain this answer?
Find the equation of a line.
1. Its x and y intercept is 2 and -2 respectively.
2. The slope of the line is 1.
1. Its x and y intercept is 2 and -2 respectively.
2. The slope of the line is 1.
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question ask
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.

|
Shivam Ghoshal answered |
In statement 1, the x and y intercept is 2 and -2 respectively, hence the line passes through (2,0) and (0,-2). The slope is
(-2 - 0)/(2 - 0) = -1.
The equation is y/(x - 2) = -1 hence x = -x + 2.
The statement is sufficient.
In statement 2, the slope is 1. Since we are not given any point where the line is passing, the statement is insufficient. Thus, Statement (1) ALONE is sufficient but statement (2) is not sufficient.
(-2 - 0)/(2 - 0) = -1.
The equation is y/(x - 2) = -1 hence x = -x + 2.
The statement is sufficient.
In statement 2, the slope is 1. Since we are not given any point where the line is passing, the statement is insufficient. Thus, Statement (1) ALONE is sufficient but statement (2) is not sufficient.
Stephenson, a businessman bought an Iron box for $80. Determine his profit.
1. He made a 30% profit.
2. His selling price was $104.- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question ask
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'D'. Can you explain this answer?
Stephenson, a businessman bought an Iron box for $80. Determine his profit.
1. He made a 30% profit.
2. His selling price was $104.
1. He made a 30% profit.
2. His selling price was $104.
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question ask
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.

|
Geetika Sarkar answered |
Cost price = $80 is equivalent to 100%.
In statement 1, profit = 30%
= 30/100 × 80 = $24.
Profit = 104 - 80 = $24. The statement is sufficient.
In statement 2, selling price = 104.
selling price = cost price + profit; hence, profit =104 - 80 = $24. The statement is sufficient.
In statement 1, profit = 30%
= 30/100 × 80 = $24.
Profit = 104 - 80 = $24. The statement is sufficient.
In statement 2, selling price = 104.
selling price = cost price + profit; hence, profit =104 - 80 = $24. The statement is sufficient.
Determine the price of two type A footballs if the total cost of a type A and a type B football is $500.
1. Type B football costs $200.
2. Two type A and three type B footballs costs $1200.- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question ask
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'D'. Can you explain this answer?
Determine the price of two type A footballs if the total cost of a type A and a type B football is $500.
1. Type B football costs $200.
2. Two type A and three type B footballs costs $1200.
1. Type B football costs $200.
2. Two type A and three type B footballs costs $1200.
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question ask
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.

|
Maya Khanna answered |
Let A and B represent the number of type A and Type B footballs respectively. Then A + B = 500.
In statement 1, B = 200, hence, from A + B = 500, A = 500 - B = 500 - 200 = $300. Thus 2A = $600. The statement is sufficient.
In statement 2, 2A + 3B = 1200, from A + B = 500,multiplying it by 3, we have 3A + 3B = 1500. Subtracting 2A + 3B = 1200 from 3A + 3B = 1500, we have A = 300; thus 2A = $600. The statement too is sufficient.
In statement 1, B = 200, hence, from A + B = 500, A = 500 - B = 500 - 200 = $300. Thus 2A = $600. The statement is sufficient.
In statement 2, 2A + 3B = 1200, from A + B = 500,multiplying it by 3, we have 3A + 3B = 1500. Subtracting 2A + 3B = 1200 from 3A + 3B = 1500, we have A = 300; thus 2A = $600. The statement too is sufficient.
A straight line L passes through (2,8) and the origin. Find the equation of a line perpendicular to L.
1. The line passes through the origin.
2. The line passes through (2,-0.5).- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question ask
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'D'. Can you explain this answer?
A straight line L passes through (2,8) and the origin. Find the equation of a line perpendicular to L.
1. The line passes through the origin.
2. The line passes through (2,-0.5).
1. The line passes through the origin.
2. The line passes through (2,-0.5).
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question ask
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.

|
Shivam Ghoshal answered |
The line L passes through (2,8) and (0,0) hence its slope is
slope = (8 - 0)/(2 - 0) = 4.
Since L is perpendicular to the line in question, the product of their slope is -1. Therefore, the slope of the line in question is -1/4.
In statement 1, the line passes the origin, (0,0) and its slope is -1/4 hence its equation is y = -x/4. The statement is sufficient.
In statement 2, line passes through the (2,0.5) and its slope is -1/4. Thus we have (y + 0.5)/(x - 2) = -1/4
y + 1/2 = -x/4 + 1/2
thus y = -x/4. The statement is sufficient too.
Thus, EACH statement ALONE is sufficient.
slope = (8 - 0)/(2 - 0) = 4.
Since L is perpendicular to the line in question, the product of their slope is -1. Therefore, the slope of the line in question is -1/4.
In statement 1, the line passes the origin, (0,0) and its slope is -1/4 hence its equation is y = -x/4. The statement is sufficient.
In statement 2, line passes through the (2,0.5) and its slope is -1/4. Thus we have (y + 0.5)/(x - 2) = -1/4
y + 1/2 = -x/4 + 1/2
thus y = -x/4. The statement is sufficient too.
Thus, EACH statement ALONE is sufficient.
Determine the volume of a cuboids.
1. The length is twice the width and the height is 4 inches.
2. The length is 6 inches.- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question ask
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'C'. Can you explain this answer?
Determine the volume of a cuboids.
1. The length is twice the width and the height is 4 inches.
2. The length is 6 inches.
1. The length is twice the width and the height is 4 inches.
2. The length is 6 inches.
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question ask
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.

|
Maya Khanna answered |
Volume = length × width × height
In statement 1, let width be x, length = 2x and height = 4
Volume = x × 2x × 4 = 8x² cubic inches. Since it is in terms of unknown value, x, it is insufficient.
In statement 2, length = 6 inches but the width and height is unknown hence it is not sufficient to determine the volume.
Combining the two statements, length = 2x = 6 hence x = 3 inches.
width = 3 inches and height = 4 inches.
Volume = 3 × 4 × 6 = 72 cubic inches. Thus , BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
In statement 1, let width be x, length = 2x and height = 4
Volume = x × 2x × 4 = 8x² cubic inches. Since it is in terms of unknown value, x, it is insufficient.
In statement 2, length = 6 inches but the width and height is unknown hence it is not sufficient to determine the volume.
Combining the two statements, length = 2x = 6 hence x = 3 inches.
width = 3 inches and height = 4 inches.
Volume = 3 × 4 × 6 = 72 cubic inches. Thus , BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
Find the value of r if 4r + 2t = 14.
1. t = 2.
2. r > t.- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question ask
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'A'. Can you explain this answer?
Find the value of r if 4r + 2t = 14.
1. t = 2.
2. r > t.
1. t = 2.
2. r > t.
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question ask
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.

|
Aditya Sharma answered |
4r + 2t = 14
In statement 1, t = 2, substituting for t in 4r + 2t = 14, we have
4r + 4 = 14; 4r = 10; r = 2 1/2. The statement is sufficient.
In statement 2, r > t , thus none of this is assigned a numeric value. Thisa implies that the solution of r in 4r + 2t = 14 will be a set of values. This implies that the statement is not sufficient.
In statement 1, t = 2, substituting for t in 4r + 2t = 14, we have
4r + 4 = 14; 4r = 10; r = 2 1/2. The statement is sufficient.
In statement 2, r > t , thus none of this is assigned a numeric value. Thisa implies that the solution of r in 4r + 2t = 14 will be a set of values. This implies that the statement is not sufficient.
A particle moving in air increases its speed within 30 minutes. Find its acceleration.
1. Its initial velocity is 20miles per hour and its final velocity is 25 miles per hour.
2. The particle increases its speed by 5 miles per hour.- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question ask
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'D'. Can you explain this answer?
A particle moving in air increases its speed within 30 minutes. Find its acceleration.
1. Its initial velocity is 20miles per hour and its final velocity is 25 miles per hour.
2. The particle increases its speed by 5 miles per hour.
1. Its initial velocity is 20miles per hour and its final velocity is 25 miles per hour.
2. The particle increases its speed by 5 miles per hour.
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question ask
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.

|
Hridoy Desai answered |
Time taken = change in time = 30 minutes = 1/2 hours
In statement 1, Initial velocity (v1) = 20 miles per hour and change in time = 0.5 hours (given)
Final velocity (v2) = 25 miles per hour.
Acceleration = (v2 - v1)/ change in time = (25 - 20)/ 0.5 = 10 miles per hour per hour. Therefore, the statement is sufficient.
In statement 2, Change in velocity = 5 miles per hour and change in time = 0.5 hours (given).
Acceleration = Change in velocity/change in time = 5/0.5 =10 miles per hour per hour. Therefore, the statement is sufficient.
Therefore, EACH statement ALONE is sufficient.
In statement 1, Initial velocity (v1) = 20 miles per hour and change in time = 0.5 hours (given)
Final velocity (v2) = 25 miles per hour.
Acceleration = (v2 - v1)/ change in time = (25 - 20)/ 0.5 = 10 miles per hour per hour. Therefore, the statement is sufficient.
In statement 2, Change in velocity = 5 miles per hour and change in time = 0.5 hours (given).
Acceleration = Change in velocity/change in time = 5/0.5 =10 miles per hour per hour. Therefore, the statement is sufficient.
Therefore, EACH statement ALONE is sufficient.
What is the cost of one pen?1. The cost of 3 pens and 2 pencils is ₹80.2. The cost of 2 pens and 2 pencils is ₹70, and each pencil costs ₹10.- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
- c)BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
- d)EACH statement ALONE is sufficient.
Correct answer is option 'C'. Can you explain this answer?
What is the cost of one pen?
1. The cost of 3 pens and 2 pencils is ₹80.
2. The cost of 2 pens and 2 pencils is ₹70, and each pencil costs ₹10.
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
c)
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
d)
EACH statement ALONE is sufficient.

|
EduRev GMAT answered |
Let cost of pen = P, pencil = Q.
From (1): 3P + 2Q = 80 — (i)
From (2): 2P + 2Q = 70 and Q = 10
Substitute Q = 10 into both equations:
From (2): 2P + 20 = 70 → 2P = 50 → P = 25
From (1): 3P + 20 = 80 → 3P = 60 → P = 20
Conflict in values shows contradiction → So both are needed to cross-verify.
From (1): 3P + 2Q = 80 — (i)
From (2): 2P + 2Q = 70 and Q = 10
Substitute Q = 10 into both equations:
From (2): 2P + 20 = 70 → 2P = 50 → P = 25
From (1): 3P + 20 = 80 → 3P = 60 → P = 20
Conflict in values shows contradiction → So both are needed to cross-verify.
s,p and q are interior angles of an Isosceles triangle. Find the value of q.
1. s = 72°.
2. p and q are base angles of the triangle.- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question ask
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'C'. Can you explain this answer?
s,p and q are interior angles of an Isosceles triangle. Find the value of q.
1. s = 72°.
2. p and q are base angles of the triangle.
1. s = 72°.
2. p and q are base angles of the triangle.
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question ask
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.

|
Shivam Ghoshal answered |
Since s, p and q are interior angles of Isosceles triangle, s + p + q = 180°.
In statement 1, If s = 72°, then p + q + 72 = 180° and
p + q = 180°.
Since we have two unknowns in one equation and we are not sure which angles are base angles, we cannot determine the value of q, hence the statement is not sufficient.
In statement 2, p and q are base angles of the triangle, hence from s + p + q = 180°, we have s + 2q = 180°, but p = q.
But the statement is not sufficient since it does not have any information about s.
Combining the two, we have s + 2q = 180° and s = 72°, we have
72° + 2q = 180°; 2q = 180 - 72 = 108°. q = 54°.
Therefore, BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
In statement 1, If s = 72°, then p + q + 72 = 180° and
p + q = 180°.
Since we have two unknowns in one equation and we are not sure which angles are base angles, we cannot determine the value of q, hence the statement is not sufficient.
In statement 2, p and q are base angles of the triangle, hence from s + p + q = 180°, we have s + 2q = 180°, but p = q.
But the statement is not sufficient since it does not have any information about s.
Combining the two, we have s + 2q = 180° and s = 72°, we have
72° + 2q = 180°; 2q = 180 - 72 = 108°. q = 54°.
Therefore, BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
In 2003, a then-nascent Internet search engine developed an indexing algorithm called G-Cache that retrieved and stored X million webpages per hour. At the same time, a competitor developed an indexing algorithm called HTML-Compress that indexed and stored Y million pages per hour. If both algorithms indexed a positive number of pages per hour, was the number of pages indexed per hour by G-Cache greater than three times the number of pages indexed by HTML-Compress?
1)On a per-hour basis in 2003, G-Cache indexed 1 million more pages than HTML-Compress indexed
2)HTML-Compress can index between 400,000 and 1.4 million pages per hour- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient
- c)BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
- d)EACH statement ALONE is sufficient.
- e)Statement (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data are needed.
Correct answer is option 'E'. Can you explain this answer?
In 2003, a then-nascent Internet search engine developed an indexing algorithm called G-Cache that retrieved and stored X million webpages per hour. At the same time, a competitor developed an indexing algorithm called HTML-Compress that indexed and stored Y million pages per hour. If both algorithms indexed a positive number of pages per hour, was the number of pages indexed per hour by G-Cache greater than three times the number of pages indexed by HTML-Compress?
1)On a per-hour basis in 2003, G-Cache indexed 1 million more pages than HTML-Compress indexed
2)HTML-Compress can index between 400,000 and 1.4 million pages per hour
1)On a per-hour basis in 2003, G-Cache indexed 1 million more pages than HTML-Compress indexed
2)HTML-Compress can index between 400,000 and 1.4 million pages per hour
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient
c)
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
d)
EACH statement ALONE is sufficient.
e)
Statement (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data are needed.

|
Niti Choudhury answered |
Translate the final sentence, which contains the question, into algebra:
"the number of pages indexed per hour by G-Cache" = X
"greater than three times" translates into: >3
"the number of pages indexed by HTML-Compress" = Y
"the number of pages indexed per hour by G-Cache" = X
"greater than three times" translates into: >3
"the number of pages indexed by HTML-Compress" = Y
Putting this together:
Was X > 3Y?
Evaluate Statement (1) alone.
Translate the information from Statement (1) into algebra:
X - Y = 1 million
Since the original question states that "both algorithms indexed a positive number of pages per hour", the following inequalities must hold true:
X > 0
Y > 0
Simply knowing that X - Y = 1 million does not provide enough information to determine whether X > 3Y.
This can be seen via an algebraic substitution or by trying different numbers.
Trying Numbers
Let X = 10 and, therefore, Y = 9
10 is NOT > 3(9)
But, let X = 1.1 and, therefore, Y = .1
1.1 IS > 3(.1)
Algebraic Substitution
X - Y = 1 million
X = Y + 1 million
Plug this into the inequality we are trying to solve for:
Was X > 3Y?
Was (Y + 1 million) > 3Y?
Was 1 million > 2Y?
Was 500,000 > Y?
Was Y < 500,000?
Was X > 3Y?
Evaluate Statement (1) alone.
Translate the information from Statement (1) into algebra:
X - Y = 1 million
Since the original question states that "both algorithms indexed a positive number of pages per hour", the following inequalities must hold true:
X > 0
Y > 0
Simply knowing that X - Y = 1 million does not provide enough information to determine whether X > 3Y.
This can be seen via an algebraic substitution or by trying different numbers.
Trying Numbers
Let X = 10 and, therefore, Y = 9
10 is NOT > 3(9)
But, let X = 1.1 and, therefore, Y = .1
1.1 IS > 3(.1)
Algebraic Substitution
X - Y = 1 million
X = Y + 1 million
Plug this into the inequality we are trying to solve for:
Was X > 3Y?
Was (Y + 1 million) > 3Y?
Was 1 million > 2Y?
Was 500,000 > Y?
Was Y < 500,000?
Simply knowing that X - Y = 1 million does not provide enough information to determine whether Y < 500,000
Since different legitimate values of Y produce different answers to the question of whether X > 3Y, Statement (1) is not sufficient.
Statement (1) is NOT SUFFICIENT.
Evaluate Statement (2) alone.
Translate the information from Statement (2) into algebra:
400,000 < Y < 1,400,000
We know nothing about the value of X.
If X were 10 million, the answer to the original question was X > 3Y? would be "yes."
If X were 100,000, the answer to the original question was X > 3Y? would be "no."
Since different legitimate values of X and Y produce different answers to the question of whether X > 3Y, Statement (2) is not sufficient.
Statement (2) is NOT SUFFICIENT.
Evaluate Statements (1) and (2) together.
With the information in Statement (1), we concluded that the original question can be boiled down to:
Is Y < 500,000?
Statement (2) says:
400,000 < Y < 1,400,000
Even when combining Statements (1) and (2), we cannot determine whether Y < 500,000
Y could be 450,000 (in which case X = 1,450,000) or Y could be 650,000 (in which case X = 1,650,000). These two different possible values of X and Y would produce different answers to the question "Was Y < 500,000?" Consequently, we would have different answers to the question "Was X > 3Y?"
Statements (1) and (2), even when taken together, are NOT SUFFICIENT.
Since Statement (1) alone is NOT SUFFICIENT, Statement (2) alone is NOT SUFFICIENT, and Statements (1) and (2), even when taken together, are NOT SUFFICIENT.
Since different legitimate values of Y produce different answers to the question of whether X > 3Y, Statement (1) is not sufficient.
Statement (1) is NOT SUFFICIENT.
Evaluate Statement (2) alone.
Translate the information from Statement (2) into algebra:
400,000 < Y < 1,400,000
We know nothing about the value of X.
If X were 10 million, the answer to the original question was X > 3Y? would be "yes."
If X were 100,000, the answer to the original question was X > 3Y? would be "no."
Since different legitimate values of X and Y produce different answers to the question of whether X > 3Y, Statement (2) is not sufficient.
Statement (2) is NOT SUFFICIENT.
Evaluate Statements (1) and (2) together.
With the information in Statement (1), we concluded that the original question can be boiled down to:
Is Y < 500,000?
Statement (2) says:
400,000 < Y < 1,400,000
Even when combining Statements (1) and (2), we cannot determine whether Y < 500,000
Y could be 450,000 (in which case X = 1,450,000) or Y could be 650,000 (in which case X = 1,650,000). These two different possible values of X and Y would produce different answers to the question "Was Y < 500,000?" Consequently, we would have different answers to the question "Was X > 3Y?"
Statements (1) and (2), even when taken together, are NOT SUFFICIENT.
Since Statement (1) alone is NOT SUFFICIENT, Statement (2) alone is NOT SUFFICIENT, and Statements (1) and (2), even when taken together, are NOT SUFFICIENT.
If both x and y are positive integers less than 100 and greater than 10, is the sum x + y a multiple of 11?
1)x -y is a multiple of 22
2)The tens digit and the units digit of x are the same; the tens digit and the units digit of y are the same- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficien
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
- c)BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient
- d)EACH statement ALONE is sufficient.
- e)Statement (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data are needed.
Correct answer is option 'B'. Can you explain this answer?
If both x and y are positive integers less than 100 and greater than 10, is the sum x + y a multiple of 11?
1)x -y is a multiple of 22
2)The tens digit and the units digit of x are the same; the tens digit and the units digit of y are the same
1)x -y is a multiple of 22
2)The tens digit and the units digit of x are the same; the tens digit and the units digit of y are the same
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficien
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
c)
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient
d)
EACH statement ALONE is sufficient.
e)
Statement (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data are needed.

|
Arnab Kumar answered |
If both x and y are multiples of 11, then both x + y and x - y will be multiples of 11. In other words, if two numbers have a common divisor, their sum and difference retain that divisor.
In case this is hard to conceptualize, consider the following examples:
42 - 18 {both numbers share a common factor of 6}
=(6*7) - (6*3)
=6(7 - 3)
=6(4)
=24 {which is a multiple of 6}
In case this is hard to conceptualize, consider the following examples:
42 - 18 {both numbers share a common factor of 6}
=(6*7) - (6*3)
=6(7 - 3)
=6(4)
=24 {which is a multiple of 6}
49 + 14 {both numbers share a common factor of 7}
=(7*7) + (7*2)
=7(7+2)
=7*9
=63 {which is a multiple of 7}
However, if x and y are not both multiples of 11, it is possible that x - y is a multiple of 11 while x + y is not a multiple of 11. For example:
68 - 46 = 22 but 68 + 46 = 114, which is not divisible by 11.
The reason x - y is a multiple of 11 but not x + y is that, in this case, x and y are not individually multiples of 11.
Evaluate Statement (1) alone.
Since x-y is a multiple of 22, x-y is a multiple of 11 and of 2 because 22=11*2
If both x and y are multiples of 11, the sum x + y will also be a multiple of 11. Consider the following examples:
44 - 22 = 22 {which is a multiple of 11 and of 22}
44 + 22 = 66 {which is a multiple of 11 and of 22}
=(7*7) + (7*2)
=7(7+2)
=7*9
=63 {which is a multiple of 7}
However, if x and y are not both multiples of 11, it is possible that x - y is a multiple of 11 while x + y is not a multiple of 11. For example:
68 - 46 = 22 but 68 + 46 = 114, which is not divisible by 11.
The reason x - y is a multiple of 11 but not x + y is that, in this case, x and y are not individually multiples of 11.
Evaluate Statement (1) alone.
Since x-y is a multiple of 22, x-y is a multiple of 11 and of 2 because 22=11*2
If both x and y are multiples of 11, the sum x + y will also be a multiple of 11. Consider the following examples:
44 - 22 = 22 {which is a multiple of 11 and of 22}
44 + 22 = 66 {which is a multiple of 11 and of 22}
88 - 66 = 22 {which is a multiple of 11 and of 22}
88 + 66 = 154 {which is a multiple of 11 and of 22}
However, if x and y are not individually divisible by 11, it is possible that x - y is a multiple of 22 (and 11) while x + y is not a multiple of 11. For example:
78 - 56 = 22 but 78 + 56 = 134 is not a multiple of 11.
Statement (1) alone is NOT SUFFICIENT.
Evaluate Statement (2) alone.
Since the tens digit and the units digit of x are the same, the range of possible values for x includes:
11, 22, 33, 44, 55, 66, 77, 88, 99
Since each of these values is a multiple of 11, x must be a multiple of 11.
Since the tens digit and the units digit of y are the same, the range of possible values for y includes:
11, 22, 33, 44, 55, 66, 77, 88, 99
Since each of these values is a multiple of 11, y must be a multiple of 11.
As demonstrated above, if both x and y are a multiple of 11, we know that both x + y and x - y will be a multiple of 11.
Statement (2) alone is SUFFICIENT.
Since Statement (1) alone is NOT SUFFICIENT and Statement (2) alone is SUFFICIENT.
88 + 66 = 154 {which is a multiple of 11 and of 22}
However, if x and y are not individually divisible by 11, it is possible that x - y is a multiple of 22 (and 11) while x + y is not a multiple of 11. For example:
78 - 56 = 22 but 78 + 56 = 134 is not a multiple of 11.
Statement (1) alone is NOT SUFFICIENT.
Evaluate Statement (2) alone.
Since the tens digit and the units digit of x are the same, the range of possible values for x includes:
11, 22, 33, 44, 55, 66, 77, 88, 99
Since each of these values is a multiple of 11, x must be a multiple of 11.
Since the tens digit and the units digit of y are the same, the range of possible values for y includes:
11, 22, 33, 44, 55, 66, 77, 88, 99
Since each of these values is a multiple of 11, y must be a multiple of 11.
As demonstrated above, if both x and y are a multiple of 11, we know that both x + y and x - y will be a multiple of 11.
Statement (2) alone is SUFFICIENT.
Since Statement (1) alone is NOT SUFFICIENT and Statement (2) alone is SUFFICIENT.
Find the direction in which the parabola y = ax2 + bx - 2 is facing.
1. a = b
2. a < 0- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question ask
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'B'. Can you explain this answer?
Find the direction in which the parabola y = ax2 + bx - 2 is facing.
1. a = b
2. a < 0
1. a = b
2. a < 0
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question ask
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.

|
Abhishek Kapoor answered |
The parabola y = ax2 + bx - 2 faces upwards when a > 0 and downwards when a < 0.
In statement 1, a = b, this does not give the numerical equivalent to a, hence it is not sufficient.
In statement 2, a < 0, hence the parabola faces downwards. Thus the statement is sufficient.
In statement 1, a = b, this does not give the numerical equivalent to a, hence it is not sufficient.
In statement 2, a < 0, hence the parabola faces downwards. Thus the statement is sufficient.
The ratio of water to alcohol in a 14 cup container is 2:5. Determine the new volume of the liquid in the container.
1. Water is increased by 14%.
2. Mixture whose ratio of water to alcohol is 4:5 is added to that in the container.- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question ask
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'A'. Can you explain this answer?
The ratio of water to alcohol in a 14 cup container is 2:5. Determine the new volume of the liquid in the container.
1. Water is increased by 14%.
2. Mixture whose ratio of water to alcohol is 4:5 is added to that in the container.
1. Water is increased by 14%.
2. Mixture whose ratio of water to alcohol is 4:5 is added to that in the container.
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question ask
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.

|
Aditya Gupta answered |
Ratio water : alcohol = 2 : 5.
To imply that water = 2/7 × 14 = 4 cups
Alcohol = 14 - 4 = 10 cups.
If water is increased by 14%, we have
new capacity of water =114/100 × 4 = 4.56 cups.
The new volume of the liquid is 10 + 4.56 cups. Hence the statement is sufficient.
In statement 2, ratio of water : alcohol = 4 : 5 but we are not told the quantity of the liquid added or the quantity of water or alcohol added, hence, the statement is not sufficient.
To imply that water = 2/7 × 14 = 4 cups
Alcohol = 14 - 4 = 10 cups.
If water is increased by 14%, we have
new capacity of water =114/100 × 4 = 4.56 cups.
The new volume of the liquid is 10 + 4.56 cups. Hence the statement is sufficient.
In statement 2, ratio of water : alcohol = 4 : 5 but we are not told the quantity of the liquid added or the quantity of water or alcohol added, hence, the statement is not sufficient.
Is 2x + 1 > 0.
1. x is an integer
2. |x| < 1.5- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question ask
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'E'. Can you explain this answer?
Is 2x + 1 > 0.
1. x is an integer
2. |x| < 1.5
1. x is an integer
2. |x| < 1.5
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question ask
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.

|
Parth Singh answered |
2x + 1 > 0
In statement 1, a is an integer, when x = -2, 2x + 1 = -3 < 0. When x = 2, 2x + 1 = 5 > 0, hence the statement is not sufficient.
In statement 2, |x| < 1.5 implies that -1.5 < x < 1.5.
When x = 1.4, 2x + 1 = 3.8 > 0. When x = -1.4, 2x + 1 = -1.8 < 0.
Hence, the statement is not sufficient.
Combining the two statements, we have, x, an integer and -1.5 < x < 1.5, considering the more strict condition, -1.5 < x < 1.5, we find that 2x + 1 < 0, when x = -1.4 and 2x + 1 > 0 when x = 1.4.
Therefore, Statements (1) and (2) TOGETHER are NOT sufficient.
In statement 1, a is an integer, when x = -2, 2x + 1 = -3 < 0. When x = 2, 2x + 1 = 5 > 0, hence the statement is not sufficient.
In statement 2, |x| < 1.5 implies that -1.5 < x < 1.5.
When x = 1.4, 2x + 1 = 3.8 > 0. When x = -1.4, 2x + 1 = -1.8 < 0.
Hence, the statement is not sufficient.
Combining the two statements, we have, x, an integer and -1.5 < x < 1.5, considering the more strict condition, -1.5 < x < 1.5, we find that 2x + 1 < 0, when x = -1.4 and 2x + 1 > 0 when x = 1.4.
Therefore, Statements (1) and (2) TOGETHER are NOT sufficient.
Find the common difference of the arithmetic sequence.
1. The third term of the sequence is 1.428.
2. The first and the fifth terms of the sequence is 1 and 1.856.- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question ask
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'B'. Can you explain this answer?
Find the common difference of the arithmetic sequence.
1. The third term of the sequence is 1.428.
2. The first and the fifth terms of the sequence is 1 and 1.856.
1. The third term of the sequence is 1.428.
2. The first and the fifth terms of the sequence is 1 and 1.856.
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question ask
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.

|
Tanishq Choudhury answered |
an = a + (n - 1)d
In statement 1, third term, a3 = a + (3 - 1)d = 1.428; a + 2d =1.428.
This is one equation with two unknowns hence we cannot determine the value of d. The statement is not sufficient.
In statement 2, a = 1 and a5 = a + (5 - 1)d = 1.856
Substituting for a, we have 1 + 4d = 1.856; d = 0.214.
The common difference is 0.214, therefore, the statement is sufficient.
In statement 1, third term, a3 = a + (3 - 1)d = 1.428; a + 2d =1.428.
This is one equation with two unknowns hence we cannot determine the value of d. The statement is not sufficient.
In statement 2, a = 1 and a5 = a + (5 - 1)d = 1.856
Substituting for a, we have 1 + 4d = 1.856; d = 0.214.
The common difference is 0.214, therefore, the statement is sufficient.
What is the value of the positive number, p?
1. One of its divisors is 7.
2. p is divisible by two positive numbers only- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question ask
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'C'. Can you explain this answer?
What is the value of the positive number, p?
1. One of its divisors is 7.
2. p is divisible by two positive numbers only
1. One of its divisors is 7.
2. p is divisible by two positive numbers only
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question ask
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.

|
Aditya Gupta answered |
In statement 1, since one of the divisor is 7, it implies that the number is a multiple of 7. This allows us to have infinitely many numbers, hence the statement is not sufficient.
In statement 2, the number is divisible by two numbers only. This implies that p is prime since a prime number is divisible by two positive numbers. Since there are infinitely many prime numbers, the statement is not sufficient.
Combining the two statements, we have p a prime number being divisible by 7, hence p must be 7. Therefore, both statements together are sufficient but neither statement alone is sufficient.
In statement 2, the number is divisible by two numbers only. This implies that p is prime since a prime number is divisible by two positive numbers. Since there are infinitely many prime numbers, the statement is not sufficient.
Combining the two statements, we have p a prime number being divisible by 7, hence p must be 7. Therefore, both statements together are sufficient but neither statement alone is sufficient.
If z = xn-19, is z divisible by 9?
1)x = 10; n is a positive integer
2)z + 981 is a multiple of 9- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
- c)BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
- d)EACH statement ALONE is sufficient.
- e)Statement (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data are needed.
Correct answer is option 'D'. Can you explain this answer?
If z = xn-19, is z divisible by 9?
1)x = 10; n is a positive integer
2)z + 981 is a multiple of 9
1)x = 10; n is a positive integer
2)z + 981 is a multiple of 9
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
c)
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
d)
EACH statement ALONE is sufficient.
e)
Statement (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data are needed.

|
Niti Choudhury answered |
In working on this question, it is helpful to remember that a number will be divisible by 9 if the sum of its digits equals 9.
Evaluate Statement (1) alone.
Based upon the information in Statement (1), it is helpful to plug in a few values and see if a pattern emerges:
101 - 19 = -9
102 - 19 = 81; the sum of the digits is 9, which is divisible by 9, meaning the entire expression is divisible by 9
103 - 19 = 981; the sum of the digits is 9 + 8 + 1=18, which is divisible by 9, meaning the entire expression is divisible by 9
104 - 19 = 9981; the sum of the digits is 9(2) + 8 + 1=27, which is divisible by 9, meaning the entire expression is divisible by 9
Notice that, in each instance, the sum of the digits is divisible by 9, meaning the entire expression is divisible by 9.
The pattern that emerges is that there are (n-2) 9s followed by the digit 8 and the digit 1.
The pattern of the sum of the digits of 10n - 19 is 9(n-2) + 9 for all values of n > 1. (For n = 1, the sum is -9, which is also divisible by 9.) This means that the sum of the digits of 10n - 19 is 9(n-1). Since this sum will always be divisible by 9, the entire expression (i.e., 10n - 19) will always be divisible by 9.
Based upon this pattern, Statement (1) is SUFFICIENT.
Evaluate Statement (2) alone.
Statement (2) says that z + 981 is a multiple of 9. This can be translated into algebra: 9(a constant integer) = z + 981
Divide both sides by 9
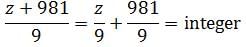
Since 981 is divisible by 9 (its digits sum to 18, which is divisible by 9), you can further rewrite Statement (2).
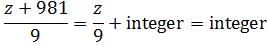
Since an integer minus an integer is an integer, Statement (2) can be rewritten even further. Since z divided by 9 is an integer, z is divisible by 9. Statement (2) is SUFFICIENT.

Since Statement (1) alone is SUFFICIENT and Statement (2) alone is SUFFICIENT.
Evaluate Statement (1) alone.
Based upon the information in Statement (1), it is helpful to plug in a few values and see if a pattern emerges:
101 - 19 = -9
102 - 19 = 81; the sum of the digits is 9, which is divisible by 9, meaning the entire expression is divisible by 9
103 - 19 = 981; the sum of the digits is 9 + 8 + 1=18, which is divisible by 9, meaning the entire expression is divisible by 9
104 - 19 = 9981; the sum of the digits is 9(2) + 8 + 1=27, which is divisible by 9, meaning the entire expression is divisible by 9
Notice that, in each instance, the sum of the digits is divisible by 9, meaning the entire expression is divisible by 9.
The pattern that emerges is that there are (n-2) 9s followed by the digit 8 and the digit 1.
The pattern of the sum of the digits of 10n - 19 is 9(n-2) + 9 for all values of n > 1. (For n = 1, the sum is -9, which is also divisible by 9.) This means that the sum of the digits of 10n - 19 is 9(n-1). Since this sum will always be divisible by 9, the entire expression (i.e., 10n - 19) will always be divisible by 9.
Based upon this pattern, Statement (1) is SUFFICIENT.
Evaluate Statement (2) alone.
Statement (2) says that z + 981 is a multiple of 9. This can be translated into algebra: 9(a constant integer) = z + 981
Divide both sides by 9
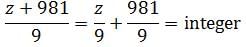
Since 981 is divisible by 9 (its digits sum to 18, which is divisible by 9), you can further rewrite Statement (2).
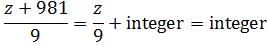
Since an integer minus an integer is an integer, Statement (2) can be rewritten even further. Since z divided by 9 is an integer, z is divisible by 9. Statement (2) is SUFFICIENT.

Since Statement (1) alone is SUFFICIENT and Statement (2) alone is SUFFICIENT.
If w, x, y, and z are the digits of the four-digit number N, a positive integer, what is the remainder when N is divided by 9?
1) w + x + y + z = 13
2) N + 5 is divisible by 9- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
- c)BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
- d)EACH statement ALONE is sufficient.
- e)Statement (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data are needed.
Correct answer is option 'D'. Can you explain this answer?
If w, x, y, and z are the digits of the four-digit number N, a positive integer, what is the remainder when N is divided by 9?
1) w + x + y + z = 13
2) N + 5 is divisible by 9
1) w + x + y + z = 13
2) N + 5 is divisible by 9
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
c)
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
d)
EACH statement ALONE is sufficient.
e)
Statement (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data are needed.

|
Sreemoyee Nambiar answered |
Analysis:
Statement 1:
- The sum of the digits is 13.
- However, this information alone does not provide the exact value of the number N.
- Therefore, statement 1 alone is not sufficient.
Statement 2:
- N + 5 is divisible by 9.
- This implies that the remainder when N is divided by 9 is 4.
- Therefore, statement 2 alone is sufficient.
Combined Statements:
- Combining the two statements, we know that the sum of the digits is 13 and the remainder when N is divided by 9 is 4.
- Since the remainder when N is divided by 9 is 4, the sum of the digits must be congruent to 4 modulo 9.
- The only combination of digits that satisfies this condition is 4, 4, 2, 3.
- Therefore, each statement alone is sufficient to determine the remainder when N is divided by 9.
- The correct answer is option D.
Is the number a prime number?
1. The number is divisible by a prime factor.
2. The number is positive- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question ask
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'E'. Can you explain this answer?
Is the number a prime number?
1. The number is divisible by a prime factor.
2. The number is positive
1. The number is divisible by a prime factor.
2. The number is positive
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question ask
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.

|
Bhavana Kulkarni answered |
In statement 1, the number is divisible by a prime factor, hence the number can be 2, 4, 6, -2, -4, -6, 8 , 9 . . . . Hence the statement is insufficient.
In statement 2, the number is positive. But there are infinitely many numbers that are positive but not prime, hence, the statement is not sufficient.
Combining the two statements, we have the numbers being positive, thus, 2,4,6,8,9,10,. . . . The numbers are infinitely many, hence Statements (1) and (2) TOGETHER are NOT sufficient.
In statement 2, the number is positive. But there are infinitely many numbers that are positive but not prime, hence, the statement is not sufficient.
Combining the two statements, we have the numbers being positive, thus, 2,4,6,8,9,10,. . . . The numbers are infinitely many, hence Statements (1) and (2) TOGETHER are NOT sufficient.
Find the area of a right angle triangle whose base is 12 inches.
1. The hypotenuse is 13 inches.
2. The perpendicular height of the triangle is one less than half its base.- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question ask
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'D'. Can you explain this answer?
Find the area of a right angle triangle whose base is 12 inches.
1. The hypotenuse is 13 inches.
2. The perpendicular height of the triangle is one less than half its base.
1. The hypotenuse is 13 inches.
2. The perpendicular height of the triangle is one less than half its base.
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question ask
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.

|
Hridoy Gupta answered |
Base = 12 inches.
In statement 1, hypotenuse = 13 inches. Using Pythagorean theorem, we have height = √(13² - 12²) = 5.
Area = 1/2 × 5 × 12 = 30 square inches. The statement is sufficient.
In statement 2, perpendicular height = 1/2 (base) - 1 = 1/2 × 12 -1 = 5 inches. Base = 12 inches.
Area =1/2 × 5 × 12 = 30 square inches. The statement is sufficient.
In statement 1, hypotenuse = 13 inches. Using Pythagorean theorem, we have height = √(13² - 12²) = 5.
Area = 1/2 × 5 × 12 = 30 square inches. The statement is sufficient.
In statement 2, perpendicular height = 1/2 (base) - 1 = 1/2 × 12 -1 = 5 inches. Base = 12 inches.
Area =1/2 × 5 × 12 = 30 square inches. The statement is sufficient.
Determine the value of t.
1. 2t + 6s = 8
2. t/2 - 2 = - 3s/4- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question ask
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'E'. Can you explain this answer?
Determine the value of t.
1. 2t + 6s = 8
2. t/2 - 2 = - 3s/4
1. 2t + 6s = 8
2. t/2 - 2 = - 3s/4
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question ask
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.

|
Abhishek Kapoor answered |
In statement 1, 2t + 6s = 8 is one equation is two unknowns, hence we cannot determine the value of t. The statement is insufficient.
In statement 2, t/2 - 2 = -3s/4 can be transformed to t - 4 = -6s/2. But this is an equation with two unknowns hence we cannot determine the value of t. The statement is insufficient.
Combining the two statements, we have 2, t/2 - 2 = -3s/4 which can be transformed to t - 4 = -6s/2 then to 2t - 8 = -6s but this is equal to the equation 2t + 6s = 8, hence we have an equation with two unknowns. Thus, we cannot determine the value of t; the statements (1) and (2) TOGETHER are NOT sufficient.
In statement 2, t/2 - 2 = -3s/4 can be transformed to t - 4 = -6s/2. But this is an equation with two unknowns hence we cannot determine the value of t. The statement is insufficient.
Combining the two statements, we have 2, t/2 - 2 = -3s/4 which can be transformed to t - 4 = -6s/2 then to 2t - 8 = -6s but this is equal to the equation 2t + 6s = 8, hence we have an equation with two unknowns. Thus, we cannot determine the value of t; the statements (1) and (2) TOGETHER are NOT sufficient.

If angle ABC is 30 degrees, what is the area of triangle BCE?
1)Angle CDF is 120 degrees, lines L and M are parallel, and AC = 6, BC = 12, and EC = 2AC
2)Angle DCG is 60 degrees, angle CDG is 30 degrees, angle FDG = 90, and GC = 6, CD = 12 and EC = 12- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
- c)BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
- d) EACH statement ALONE is sufficient.
- e)Statement (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data are needed.
Correct answer is option 'D'. Can you explain this answer?

If angle ABC is 30 degrees, what is the area of triangle BCE?
1)Angle CDF is 120 degrees, lines L and M are parallel, and AC = 6, BC = 12, and EC = 2AC
2)Angle DCG is 60 degrees, angle CDG is 30 degrees, angle FDG = 90, and GC = 6, CD = 12 and EC = 12
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
c)
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
d)
EACH statement ALONE is sufficient.
e)
Statement (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data are needed.

|
Pranav Das answered |
Even though lines L and M look parallel and angle BAC looks like a right angle, you cannot make these assumptions.
The formula for the area of a triangle is .5bh
Evaluate Statement (1) alone.
Since EC = 2AC, EA = CA, EC = 2(6) = 12 and line AB is an angle bisector of angle EBC. This means that angle ABC = angle ABE. Since we know that angle ABC = 30, we know that angle ABE = 30. Further, since lines L and M are parallel, we know that line AB is perpendicular to line EC, meaning angle BAC is 90.
Since all the interior angles of a triangle must sum to 180:
angle ABC + angle BCA + angle BAC = 180
30 + angle BCA + 90 = 180
angle BCA = 60
Since all the interior angles of a triangle must sum to 180:
angle BCA + angle ABC + angle ABE + angle AEB = 180
60 + 30 + 30 + angle AEB = 180
angle AEB = 60
This means that triangle BCA is an equilateral triangle.
To find the area of triangle BCE, we need the base (= 12 from above) and the height, i.e., line AB. Since we know BC and AC and triangle ABC is a right triangle, we can use the Pythagorean theorem on triangle ABC to find the length of AB.
62 + (AB)2 = 122
AB2 = 144 - 36 = 108
AB = 1081/2
Area = .5bh
Area = .5(12)(1081/2) = 6*1081/2
Statement (1) is SUFFICIENT
Evaluate Statement (2) alone.
The sum of the interior angles of any triangle must be 180 degrees.
DCG + GDC + CGD = 180
60 + 30 + CGD = 180
CGD = 90
Triangle CGD is a right triangle.
Using the Pythagorean theorem, DG = 1081/2
(CG)2 + (DG)2 = (CD)2
62 + (DG)2 = 122
DG = 1081/2
At this point, it may be tempting to use DG = 1081/2 as the height of the triangle BCE, assuming that lines AB and DG are parallel and therefore AB = 1081/2 is the height of triangle BCE. However, we must show two things before we can use AB = 1081/2 as the height of triangle BCE: (1) lines L and M are parallel and (2) AB is the height of triangle BCE (i.e., angle BAC is 90 degrees).
Lines L and M must be parallel since angles FDG and CGD are equal and these two angles are alternate interior angles formed by cutting two lines with a transversal. If two alternate interior angles are equal, we know that the two lines that form the angles (lines L and M) when cut by a transversal (line DG) must be parallel.
Since lines L and M are parallel, DG = the height of triangle BCE = 1081/2. Note that it is not essential to know whether AB is the height of triangle BCE. It is sufficient to know that the height is 1081/2. To reiterate, we know that the height is 8 since the height of BCE is parallel to line DG, which is 1081/2.
Since we know both the height (1081/2) and the base (CE = 12) of triangle BCE, we know that the area is: .5*12*1081/2 = 6*1081/2
Statement (2) alone is SUFFICIENT.
Since Statement (1) alone is SUFFICIENT and Statement (2) alone is SUFFICIENT
The formula for the area of a triangle is .5bh
Evaluate Statement (1) alone.
Since EC = 2AC, EA = CA, EC = 2(6) = 12 and line AB is an angle bisector of angle EBC. This means that angle ABC = angle ABE. Since we know that angle ABC = 30, we know that angle ABE = 30. Further, since lines L and M are parallel, we know that line AB is perpendicular to line EC, meaning angle BAC is 90.
Since all the interior angles of a triangle must sum to 180:
angle ABC + angle BCA + angle BAC = 180
30 + angle BCA + 90 = 180
angle BCA = 60
Since all the interior angles of a triangle must sum to 180:
angle BCA + angle ABC + angle ABE + angle AEB = 180
60 + 30 + 30 + angle AEB = 180
angle AEB = 60
This means that triangle BCA is an equilateral triangle.
To find the area of triangle BCE, we need the base (= 12 from above) and the height, i.e., line AB. Since we know BC and AC and triangle ABC is a right triangle, we can use the Pythagorean theorem on triangle ABC to find the length of AB.
62 + (AB)2 = 122
AB2 = 144 - 36 = 108
AB = 1081/2
Area = .5bh
Area = .5(12)(1081/2) = 6*1081/2
Statement (1) is SUFFICIENT
Evaluate Statement (2) alone.
The sum of the interior angles of any triangle must be 180 degrees.
DCG + GDC + CGD = 180
60 + 30 + CGD = 180
CGD = 90
Triangle CGD is a right triangle.
Using the Pythagorean theorem, DG = 1081/2
(CG)2 + (DG)2 = (CD)2
62 + (DG)2 = 122
DG = 1081/2
At this point, it may be tempting to use DG = 1081/2 as the height of the triangle BCE, assuming that lines AB and DG are parallel and therefore AB = 1081/2 is the height of triangle BCE. However, we must show two things before we can use AB = 1081/2 as the height of triangle BCE: (1) lines L and M are parallel and (2) AB is the height of triangle BCE (i.e., angle BAC is 90 degrees).
Lines L and M must be parallel since angles FDG and CGD are equal and these two angles are alternate interior angles formed by cutting two lines with a transversal. If two alternate interior angles are equal, we know that the two lines that form the angles (lines L and M) when cut by a transversal (line DG) must be parallel.
Since lines L and M are parallel, DG = the height of triangle BCE = 1081/2. Note that it is not essential to know whether AB is the height of triangle BCE. It is sufficient to know that the height is 1081/2. To reiterate, we know that the height is 8 since the height of BCE is parallel to line DG, which is 1081/2.
Since we know both the height (1081/2) and the base (CE = 12) of triangle BCE, we know that the area is: .5*12*1081/2 = 6*1081/2
Statement (2) alone is SUFFICIENT.
Since Statement (1) alone is SUFFICIENT and Statement (2) alone is SUFFICIENT
What is the value of x?
1)The average (arithmetic mean) of 5, x2, 2, 10x, and 3 is -3
2)The medianof 109, -32, -30, 208, -15, x, 10, -43, 7 is -5
- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
- c)BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
- d)EACH statement ALONE is sufficient.
- e)Statement (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data are needed.
Correct answer is option 'D'. Can you explain this answer?
What is the value of x?
1)The average (arithmetic mean) of 5, x2, 2, 10x, and 3 is -3
2)The medianof 109, -32, -30, 208, -15, x, 10, -43, 7 is -5
1)The average (arithmetic mean) of 5, x2, 2, 10x, and 3 is -3
2)The medianof 109, -32, -30, 208, -15, x, 10, -43, 7 is -5
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
c)
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
d)
EACH statement ALONE is sufficient.
e)
Statement (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data are needed.

|
Athul Joshi answered |
Evaluate Statement (1) alone.
Based upon the formula for the average, you know that:
(5 + x2 + 2 + 10x + 3)/5 = -3
x2 + 10x + 5 + 2 + 3 = -15
x2 + 10x + 5 + 2 + 3 + 15 = 0
x2 + 10x + 25 = 0
(x + 5)2 = 0
x = -5
Statement (1) alone is SUFFICIENT.
Evaluate Statement (2) alone.
2) The median of 109, -32, -30, 208, -15, x, 10, -43, 7 is -5
Notice that the given list of numbers has 9 numbers. So median must be the 5th number when all numbers are arranged in increasing order. Median is -5 but none of the numbers are -5. Hence x must be -5. Sufficient alone.
Statement (2) alone is SUFFICIENT.
Since Statement (1) alone is SUFFICIENT and Statement (2) alone is SUFFICIENT
Based upon the formula for the average, you know that:
(5 + x2 + 2 + 10x + 3)/5 = -3
x2 + 10x + 5 + 2 + 3 = -15
x2 + 10x + 5 + 2 + 3 + 15 = 0
x2 + 10x + 25 = 0
(x + 5)2 = 0
x = -5
Statement (1) alone is SUFFICIENT.
Evaluate Statement (2) alone.
2) The median of 109, -32, -30, 208, -15, x, 10, -43, 7 is -5
Notice that the given list of numbers has 9 numbers. So median must be the 5th number when all numbers are arranged in increasing order. Median is -5 but none of the numbers are -5. Hence x must be -5. Sufficient alone.
Statement (2) alone is SUFFICIENT.
Since Statement (1) alone is SUFFICIENT and Statement (2) alone is SUFFICIENT
If x and y are positive integers, is the following cube root an integer?
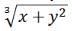 1)x = y2(y-1)
1)x = y2(y-1)
2)x = 2- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
- c)BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
- d)EACH statement ALONE is sufficient.
- e)Statement (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data are needed.
Correct answer is option 'A'. Can you explain this answer?
If x and y are positive integers, is the following cube root an integer?
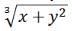
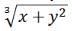
1)x = y2(y-1)
2)x = 2
2)x = 2
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
c)
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
d)
EACH statement ALONE is sufficient.
e)
Statement (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data are needed.

|
Amar Chakraborty answered |
Evaluate Statement (1) alone.
Substitute the value of x from Statement (1) into the equation and manipulate it algebraically.
Since the question says that y is a positive integer, you know that the cube root of y3, which equals y, will also be a positive integer. Statement (1) is SUFFICIENT.
Evaluate Statement (1) alone (Alternative Method).
For the cube root of a number to be an integer, that number must be an integer cubed. Consequently, the simplified version of this question is: "is x + y2 equal to an integer cubed?"
Statement (1) can be re-arranged as follows:
x = y3 - y2
y3 = x + y2
Since y is an integer, the cube root of y3, which equals y, will also be an integer.
Since y3 = x + y2, the cube root of x + y2 will also be an integer. Therefore, the following will always be an integer:
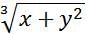
Statement (1) alone is SUFFICIENT.
Evaluate Statement (2) alone.
Statement (2) provides minimal information. The question can be written as: "is the following cube root an integer?"

If y = 4, x + y2 = 2 + 42 = 18 and the cube root of 18 is not an integer. However, if y = 5, x + y2 = 2 + 52 = 27 and the cube root of 27 is an integer. Statement (2) is NOT SUFFICIENT.
Since Statement (1) alone is SUFFICIENT and Statement (2) alone is NOT SUFFICIENT
Substitute the value of x from Statement (1) into the equation and manipulate it algebraically.
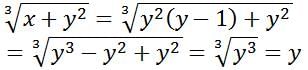
Since the question says that y is a positive integer, you know that the cube root of y3, which equals y, will also be a positive integer. Statement (1) is SUFFICIENT.
Evaluate Statement (1) alone (Alternative Method).
For the cube root of a number to be an integer, that number must be an integer cubed. Consequently, the simplified version of this question is: "is x + y2 equal to an integer cubed?"
Statement (1) can be re-arranged as follows:
x = y3 - y2
y3 = x + y2
Since y is an integer, the cube root of y3, which equals y, will also be an integer.
Since y3 = x + y2, the cube root of x + y2 will also be an integer. Therefore, the following will always be an integer:
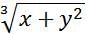
Statement (1) alone is SUFFICIENT.
Evaluate Statement (2) alone.
Statement (2) provides minimal information. The question can be written as: "is the following cube root an integer?"

If y = 4, x + y2 = 2 + 42 = 18 and the cube root of 18 is not an integer. However, if y = 5, x + y2 = 2 + 52 = 27 and the cube root of 27 is an integer. Statement (2) is NOT SUFFICIENT.
Since Statement (1) alone is SUFFICIENT and Statement (2) alone is NOT SUFFICIENT
Chapter doubts & questions for Mock Test: Data Sufficiency - Data Insights for GMAT 2025 is part of GMAT exam preparation. The chapters have been prepared according to the GMAT exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for GMAT 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Mock Test: Data Sufficiency - Data Insights for GMAT in English & Hindi are available as part of GMAT exam.
Download more important topics, notes, lectures and mock test series for GMAT Exam by signing up for free.
Data Insights for GMAT
24 videos|28 docs|21 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup









