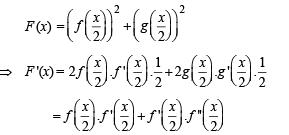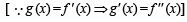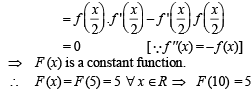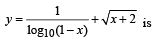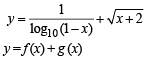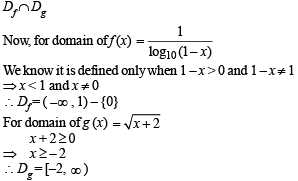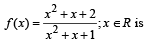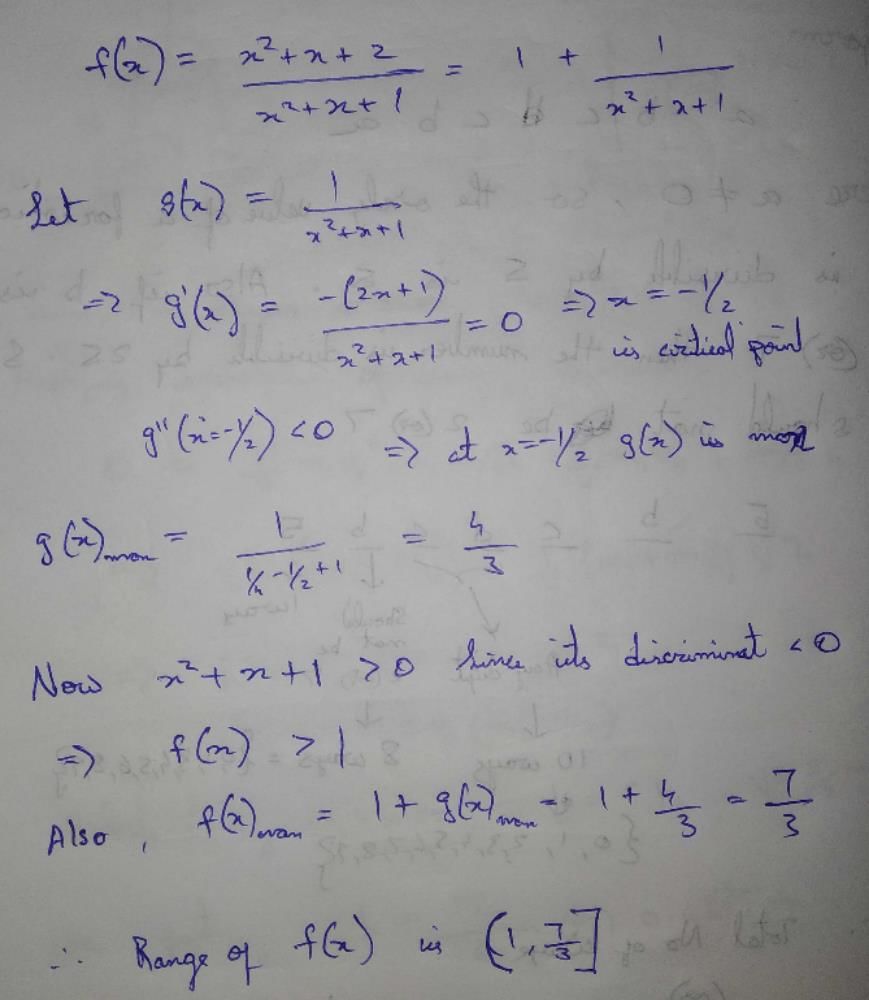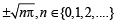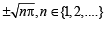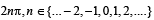All Exams >
JEE >
35 Years Chapter wise Previous Year Solved Papers for JEE >
All Questions
All questions of Functions for JEE Exam
Let a ∈ R and let f : R → R be given by f (x) = x5 – 5x + a. Then- a)f(x) has three real roots if a > 4
- b)f(x) has only real root if a > 4
- c)f x) has three real roots if a < – 4
- d)f(x) has three real roots if – 4 < a < 4
Correct answer is option 'B,D'. Can you explain this answer?
Let a ∈ R and let f : R → R be given by f (x) = x5 – 5x + a. Then
a)
f(x) has three real roots if a > 4
b)
f(x) has only real root if a > 4
c)
f x) has three real roots if a < – 4
d)
f(x) has three real roots if – 4 < a < 4
|
|
Anushka Roy answered |
f (x) = x5 - 5 x+a
f (x) = 0 ⇒ x5 - 5 x +a = 0
⇒ a = 5x – x5 = g(x)
⇒ g(x) = 0 when x = 0, 51/4 - 51/4 and g' (x ) = 0 ⇒ x = 1, – 1
Also g (– 1) = – 4 and g(1) = 4
∴ graph of g(x) will be as shown below.
From graph
f (x) = 0 ⇒ x5 - 5 x +a = 0
⇒ a = 5x – x5 = g(x)
⇒ g(x) = 0 when x = 0, 51/4 - 51/4 and g' (x ) = 0 ⇒ x = 1, – 1
Also g (– 1) = – 4 and g(1) = 4
∴ graph of g(x) will be as shown below.
From graph
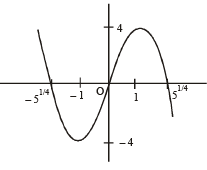
if a ∈ ( -4,-4)
then g(x) = a or f (x) = 0 has 3 real roots If a > 4 or a < – 4
then f(x) = 0 has only one real root.
∴ (b) and (d) are the correct options.
then g(x) = a or f (x) = 0 has 3 real roots If a > 4 or a < – 4
then f(x) = 0 has only one real root.
∴ (b) and (d) are the correct options.
The entire graphs of the equation y = x2 + kx – x + 9 is strictly above the x-axis if and only if- a)k < 7
- b)– 5 < k < 7
- c)k > – 5
- d)None of these.
Correct answer is option 'B'. Can you explain this answer?
The entire graphs of the equation y = x2 + kx – x + 9 is strictly above the x-axis if and only if
a)
k < 7
b)
– 5 < k < 7
c)
k > – 5
d)
None of these.
|
|
Pallavi Das answered |
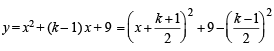
For entire graph to be above x-axis, we should have
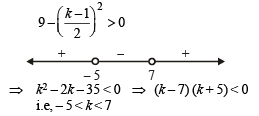
The domain of sin-1 [log3 (x/3)] is- a)[1, 9]
- b)[–1, 9]
- c)[–9, 1]
- d)[–9, –1]
Correct answer is option 'A'. Can you explain this answer?
The domain of sin-1 [log3 (x/3)] is
a)
[1, 9]
b)
[–1, 9]
c)
[–9, 1]
d)
[–9, –1]

|
Asha Nair answered |
Domain of sin-1x is [-1,1]
Therefore, -1 ≤ log3(x/3) ≤ 1
3-1 ≤ x/3 ≤ 3
1 ≤ x ≤ 9
Therefore, the domain of sin-1[log3(x/3)] is [1,9]
Let f(x) = ( x + 1)2 – 1,x > –1Statement -1 : The set {x : f(x) = f –1(x) = {0, –1}Statement-2 : f is a bijection.- a)Statement-1 is true, Statement-2 is true.Statement-2 is not a correct explanation for Statement-1.
- b)Statement-1 is true, Statement-2 is false.
- c)Statement-1 is false, Statement-2 is False.
- d)Statement-1 is False, Statement-2 is true.Statement-2 is not a correct explanation for Statement-1.
Correct answer is option 'B'. Can you explain this answer?
Let f(x) = ( x + 1)2 – 1,x > –1
Statement -1 : The set {x : f(x) = f –1(x) = {0, –1}
Statement-2 : f is a bijection.
a)
Statement-1 is true, Statement-2 is true.Statement-2 is not a correct explanation for Statement-1.
b)
Statement-1 is true, Statement-2 is false.
c)
Statement-1 is false, Statement-2 is False.
d)
Statement-1 is False, Statement-2 is true.Statement-2 is not a correct explanation for Statement-1.

|
Sai Chakraborty answered |
Given that f (x) = (x + 1)2 –1, x > –1 Clearly Df = [–, ∞) but co-demain is not given.
Therefore f (x) need not be necessarily onto.
But if f (x) is onto then as f (x) is one one also, (x + 1) being something +ve, f–1(x) will exist where (x + 1)2 –1 = y
Therefore f (x) need not be necessarily onto.
But if f (x) is onto then as f (x) is one one also, (x + 1) being something +ve, f–1(x) will exist where (x + 1)2 –1 = y
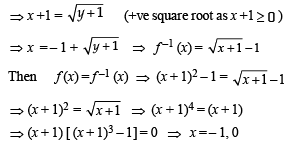
∴ The statement-1 is correct but statement-2 is false.
Let f : R → R be any function. Define g : R → R by g(x) = |f(x)| for all x. Then g is- a)onto if f is onto
- b)one-one if f is one-one
- c)continuous if f is continuous
- d)differentiable if f is differentiable.
Correct answer is option 'C'. Can you explain this answer?
Let f : R → R be any function. Define g : R → R by g(x) = |f(x)| for all x. Then g is
a)
onto if f is onto
b)
one-one if f is one-one
c)
continuous if f is continuous
d)
differentiable if f is differentiable.
|
|
Ameya Menon answered |
Let h (x) = |x| then g (x) = |f (x)| = h (f (x))
Since composition of two continuous functions is continuous, therefore g is continuous if f is continuous.
Since composition of two continuous functions is continuous, therefore g is continuous if f is continuous.
The function f(x) = 2|x| + |x + 2| – | |x + 2| – 2 |x| has a local minimum or a local maximum at x = - a)-2
- b)-2/3
- c)2
- d)2/3
Correct answer is option 'A,B'. Can you explain this answer?
The function f(x) = 2|x| + |x + 2| – | |x + 2| – 2 |x| has a local minimum or a local maximum at x =
a)
-2
b)
-2/3
c)
2
d)
2/3
|
|
Anirudh Yadav answered |
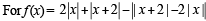
the critical points can be obtained by solving |x| = 0

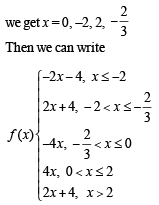
The graph of y = f(x) is as follows
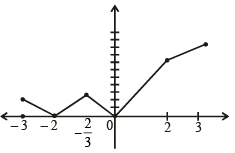
From graph f(x) has local minimum at –2 and 0 and

Th e fun ction f(x) = |px – q| + r | x |, x ∈ (-∞,∞) where p > 0, q > 0, r > 0 assumes its minimum value only on one point if- a)p ≠ q
- b)r ≠ q
- c)r ≠ p
- d)p = q = r
Correct answer is option 'C'. Can you explain this answer?
Th e fun ction f(x) = |px – q| + r | x |, x ∈ (-∞,∞) where p > 0, q > 0, r > 0 assumes its minimum value only on one point if
a)
p ≠ q
b)
r ≠ q
c)
r ≠ p
d)
p = q = r
|
|
Akanksha Sarkar answered |
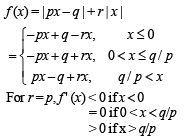
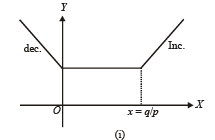
From graph (i) infinite many points for min value of f (x)
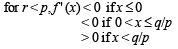
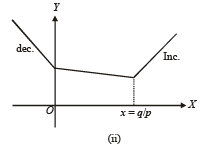
From graph (ii) only pt. of min of f (x) at x = q/p
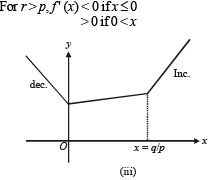
From graph (iii) only one pt. of min of f (x) at x = 0
If x satisfies |x - 1| + |x - 2| + |x - 3| > 6 , then- a)0 < x < 4
- b)x < -2 or x > 4
- c)x < 0 or x > 4
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
If x satisfies |x - 1| + |x - 2| + |x - 3| > 6 , then
a)
0 < x < 4
b)
x < -2 or x > 4
c)
x < 0 or x > 4
d)
None of these

|
Mehul Chavan answered |
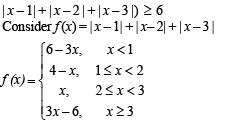
Graph of f (x) shows f (x) > 6 for x < 0 or x > 4
Let R be the set of real numbers. If f : R → R is a function defined by f (x) = x2, then f is :- a)Injective but not surjective
- b)Surjective but not injective
- c)Bijective
- d)None of these.
Correct answer is option 'D'. Can you explain this answer?
Let R be the set of real numbers. If f : R → R is a function defined by f (x) = x2, then f is :
a)
Injective but not surjective
b)
Surjective but not injective
c)
Bijective
d)
None of these.

|
Rhea Joshi answered |
f (x) = x2 is many one as f (1) = f (–1) = 1 Also f is into as – ve real number have no pre-image.
∴ F is neither injective nor surjective.
∴ F is neither injective nor surjective.
X an d Y are two sets and f : X → Y. If {f(c) = y; c ⊂ X, y ⊂ Y} and {f–1(d) = x; d ⊂ Y, x ⊂ X}, then the true statement is- a)f(f–1(b)) = b
- b)f–1(f(a)) = a
- c)f(f–1(b)) = b, b ⊂ y
- d)f–1(f(a)) = a, a ⊂ x
Correct answer is option 'D'. Can you explain this answer?
X an d Y are two sets and f : X → Y. If {f(c) = y; c ⊂ X, y ⊂ Y} and {f–1(d) = x; d ⊂ Y, x ⊂ X}, then the true statement is
a)
f(f–1(b)) = b
b)
f–1(f(a)) = a
c)
f(f–1(b)) = b, b ⊂ y
d)
f–1(f(a)) = a, a ⊂ x
|
|
Aaditya Datta answered |
Given that X and Y are two sets and f : X → Y.
{f (c) = y; c ⊂ X, y ⊂ Y} and
{f –1(d) = x : d ⊂ Y, x ⊂ X }
The pictorial representation of given information is as shown:
{f (c) = y; c ⊂ X, y ⊂ Y} and
{f –1(d) = x : d ⊂ Y, x ⊂ X }
The pictorial representation of given information is as shown:
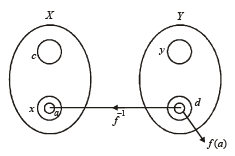
Since f –1 (d) = x ⇒ f (x) = d Now if a ⊂ x
⇒ f (a) ⊂ f (x) = d ⇒ f –1 [f (a)] = a
∴ f –1 (f (a)) = a, a ⊂ x is the correct option.
⇒ f (a) ⊂ f (x) = d ⇒ f –1 [f (a)] = a
∴ f –1 (f (a)) = a, a ⊂ x is the correct option.
L et f : (– 1, 1) → B , be a function defined by 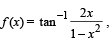 then f is both one - one and onto when B is the interval
then f is both one - one and onto when B is the interval- a)
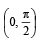
- b)
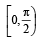
- c)
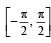
- d)
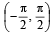
Correct answer is option 'D'. Can you explain this answer?
L et f : (– 1, 1) → B , be a function defined by 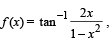 then f is both one - one and onto when B is the interval
then f is both one - one and onto when B is the interval
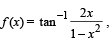 then f is both one - one and onto when B is the interval
then f is both one - one and onto when B is the intervala)
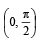
b)
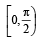
c)
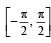
d)
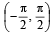

|
Asha Nair answered |
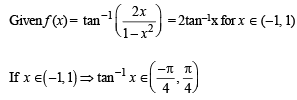
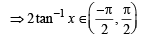
Clearly, range of f (x)
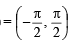
For f to be onto, codomain = range
∴ Co-domain of function
∴ Co-domain of function

The graph of the function y = f(x) is symmetrical about the line x = 2, then- a)f (x) = - f (-x)
- b)f (2 +x) = f (2-x)
- c)f (x) = f (-x)
- d)f (x +2) = f (x-2)
Correct answer is option 'B'. Can you explain this answer?
The graph of the function y = f(x) is symmetrical about the line x = 2, then
a)
f (x) = - f (-x)
b)
f (2 +x) = f (2-x)
c)
f (x) = f (-x)
d)
f (x +2) = f (x-2)

|
Ashwini Chakraborty answered |
Let us consider a graph symm. with respect to line x = 2 as shown in the figure.
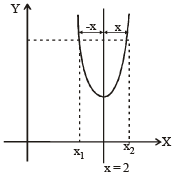
From the figure
f (x1) = f (x2), where x1 = 2-x and x2 = 2+x
∴ f (2 - x) = f (2+x)
∴ f (2 - x) = f (2+x)
A function f from the set of natural numbers to integers defined by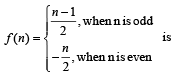
- a) neither one -one nor onto
- b) one-one but not onto
- c) onto but not one-one
- d) one-one and onto both.
Correct answer is option 'D'. Can you explain this answer?
A function f from the set of natural numbers to integers defined by
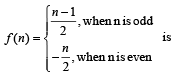
a)
neither one -one nor onto
b)
one-one but not onto
c)
onto but not one-one
d)
one-one and onto both.

|
Ishita Deshpande answered |
We have f: N →I
If x and y are two even natural numbers,
If x and y are two even natural numbers,
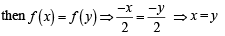
Again if x and y are two odd natural numbers then
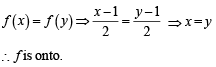
Also each negative integer is an image of even natural number and each positive integer is an image of odd natural number.
∴ f is onto.
Hence f is one one and onto both.
Hence f is one one and onto both.
If the functions f(x) and g(x) are defined on R → R such that
- a)one-one & on to
- b)neither one-one nor onto
- c)one-one but not on to
- d)on to but not one-one
Correct answer is option 'A'. Can you explain this answer?
If the functions f(x) and g(x) are defined on R → R such that

a)
one-one & on to
b)
neither one-one nor onto
c)
one-one but not on to
d)
on to but not one-one
|
|
Parth Yadav answered |
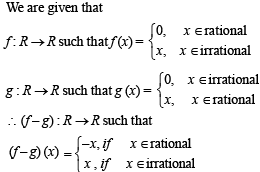
Since f – g : R → R for any x there is only one value of (f (x) – g(x)) whether x is rational or irrational.
Moreover as x∈R, f (x) – g (x) also belongs to R.
Therefore, (f – g) is one-one onto.
Moreover as x∈R, f (x) – g (x) also belongs to R.
Therefore, (f – g) is one-one onto.
 R be given by f (x) = (log(sec x + tan x))3.Then
R be given by f (x) = (log(sec x + tan x))3.Then- a)f (x) is an odd function
- b)f (x) is one-one function
- c)f (x) is an onto function
- d)f (x) is an even function
Correct answer is option 'A,B,C'. Can you explain this answer?
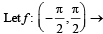 R be given by f (x) = (log(sec x + tan x))3.
R be given by f (x) = (log(sec x + tan x))3.Then
a)
f (x) is an odd function
b)
f (x) is one-one function
c)
f (x) is an onto function
d)
f (x) is an even function
|
|
Abhishek Majumdar answered |
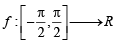
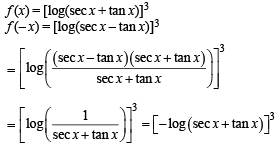
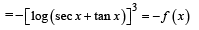
∴ f is an odd function.
(a) is correct and (d) is not correct.
Also
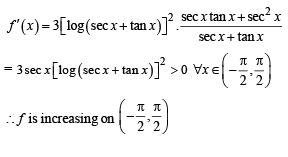
We know that strictly increasing function is one one.
∴ f is one one
∴ (b) is correct

∴ Range of f = (–∞, ∞) = R
∴ f is an onto function.
∴ (c) is correct.
∴ f is an onto function.
∴ (c) is correct.
For real x, let f (x) = x3 + 5x + 1, then- a)f is onto R but not one-one
- b)f is one-one and onto R
- c)f is neither one-one nor onto R
- d)f is one-one but not onto R
Correct answer is option 'B'. Can you explain this answer?
For real x, let f (x) = x3 + 5x + 1, then
a)
f is onto R but not one-one
b)
f is one-one and onto R
c)
f is neither one-one nor onto R
d)
f is one-one but not onto R

|
Ameya Tiwari answered |
Given that f (x) = x3 + 5x + 1
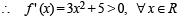
⇒ f (x) is strictly increasing on R
⇒ f (x) is one one
∴ Being a polynomial f (x) is cont. and inc.
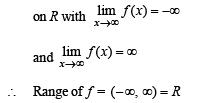
Hence f is onto also. So, f is one one and onto R.
A function is matched below against an interval where it is supposed to be increasing. Which of the following pairs is incorrectly matched?
- a)a
- b)b
- c)c
- d)d
Correct answer is option 'C'. Can you explain this answer?
A function is matched below against an interval where it is supposed to be increasing. Which of the following pairs is incorrectly matched?

a)
a
b)
b
c)
c
d)
d

|
Baishali Chakraborty answered |
Clearly function f (x) = 3x2 - 2x+1 is increasing when
f ' (x) = 6x – 2 > 0 ⇒ x ∈[1 / 3,∞)
f ' (x) = 6x – 2 > 0 ⇒ x ∈[1 / 3,∞)
∴ f (x) is incorrectly matched with 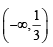
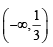
Which of the following functions is periodic?- a)f(x) = x – [x] where [x] denotes the largest integer less than or equal to the real number x
- b)
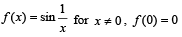
- c)f(x) = x cosx
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
Which of the following functions is periodic?
a)
f(x) = x – [x] where [x] denotes the largest integer less than or equal to the real number x
b)
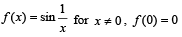
c)
f(x) = x cosx
d)
none of these
|
|
Siddharth Ghosh answered |
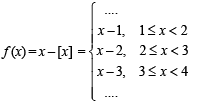
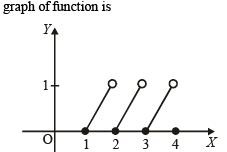
Clearly it is a periodic function with period 1.
∴ (a) is the correct alternative.
∴ (a) is the correct alternative.
Let g (x) be a function defined on [– 1, 1]. If the area of the equilateral triangle with two of its vertices at (0,0) and 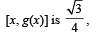 then the function g(x) is
then the function g(x) is- a)
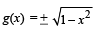
- b)
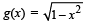
- c)
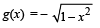
- d)
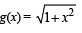
Correct answer is option 'B,C'. Can you explain this answer?
Let g (x) be a function defined on [– 1, 1]. If the area of the equilateral triangle with two of its vertices at (0,0) and 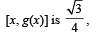 then the function g(x) is
then the function g(x) is
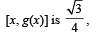 then the function g(x) is
then the function g(x) isa)
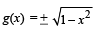
b)
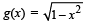
c)
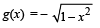
d)
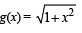
|
|
Palak Joshi answered |
As (0, 0) and (x, g (x)) are two vertices of an equilateral triangle; therefore, length of the side of D is
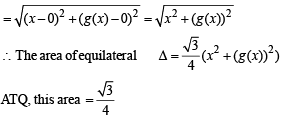
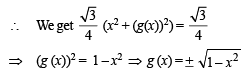
∴ (b), (c) are the correct answers as (a) is not a function
(∴ image of x is not unique)
Let f(x) = sin x and g(x) = ln | x |. If th e ran ges of th e composition functions fog and gof are R1 and R2 respectively, th en- a)R1 = {u : -1 < u < 1}, R2 ={v : - ∞ < v < 0}
- b)R1 = {u : - ∞ < u < 0}, R2 = {v : -1 < v < 0}
- c)R1 = {u : -1 < u < 1}, R2 ={v : - ∞ < v < 0}
- d)R1 = {u : -1 < u < 1}, R2 ={v : - ∞ < v < 0}
Correct answer is option 'D'. Can you explain this answer?
Let f(x) = sin x and g(x) = ln | x |. If th e ran ges of th e composition functions fog and gof are R1 and R2 respectively, th en
a)
R1 = {u : -1 < u < 1}, R2 ={v : - ∞ < v < 0}
b)
R1 = {u : - ∞ < u < 0}, R2 = {v : -1 < v < 0}
c)
R1 = {u : -1 < u < 1}, R2 ={v : - ∞ < v < 0}
d)
R1 = {u : -1 < u < 1}, R2 ={v : - ∞ < v < 0}
|
|
Om Verma answered |
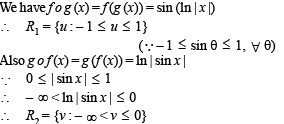
Let f, g and h be real-valued functions defined on the interval 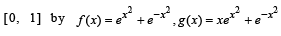 and
and 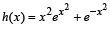 . If a, b and c denote, respectively, the absolute maximum of f, g and h on [0, 1], then
. If a, b and c denote, respectively, the absolute maximum of f, g and h on [0, 1], then- a)a = b and c ≠ b
- b)a = c and a ≠ b
- c)a ≠ b and c ≠ b
- d)a = b = c
Correct answer is option 'D'. Can you explain this answer?
Let f, g and h be real-valued functions defined on the interval 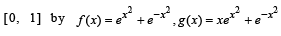 and
and 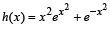 . If a, b and c denote, respectively, the absolute maximum of f, g and h on [0, 1], then
. If a, b and c denote, respectively, the absolute maximum of f, g and h on [0, 1], then
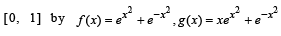 and
and 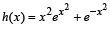 . If a, b and c denote, respectively, the absolute maximum of f, g and h on [0, 1], then
. If a, b and c denote, respectively, the absolute maximum of f, g and h on [0, 1], thena)
a = b and c ≠ b
b)
a = c and a ≠ b
c)
a ≠ b and c ≠ b
d)
a = b = c
|
|
Mira Yadav answered |
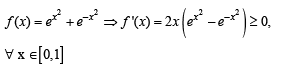
∴ f (x) is an increasing function on [ 0,1]
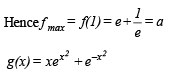
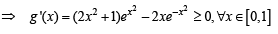
∴ g (x) is an increasing function on [ 0,1]

∴ h (x) is an increasing function on [ 0,1]
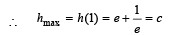
Hence a = b = c.
Let E = {1, 2, 3, 4} and F = {1, 2}. Then the number of onto functions from E to F is- a)14
- b)16
- c)12
- d)8
Correct answer is option 'A'. Can you explain this answer?
Let E = {1, 2, 3, 4} and F = {1, 2}. Then the number of onto functions from E to F is
a)
14
b)
16
c)
12
d)
8
|
|
Nikhil Sengupta answered |
From E to F we can define, in all, 2 × 2 × 2 × 2 = 16 functions (2 options for each element of E) out of which 2 are into, when all the elements of E either map to 1 or to 2.
∴ No. of onto functions = 16 – 2 = 14
∴ No. of onto functions = 16 – 2 = 14
Let f(x) = | x – 1 |. Then- a)f(x2) = (f(x))2
- b)f(x + y) = f(x) + f(y)
- c)f(| x |) = | f(x) |
- d)None of these
Correct answer is option 'D'. Can you explain this answer?
Let f(x) = | x – 1 |. Then
a)
f(x2) = (f(x))2
b)
f(x + y) = f(x) + f(y)
c)
f(| x |) = | f(x) |
d)
None of these

|
Swara Ahuja answered |
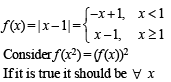
∴ Put x = 2
LHS = f (22) = |4 – 1| = 3 and RHS = ( f (2))2 = 1
∴ (a) is not correct
Consider f (x + y) = f (x) + f (y)
Put x = 2, y = 5 we get
f (7) = 6; f (2) + f (5) = 1 + 4 = 5
∴ (b) is not correct
Consider f (| x |) = | f (x) |
Put x = – 5 then f (| –5 |) = f (5) = 4
| f (– 5) | = | – 5 – 1| = 6
∴ (c) is not correct.
Hence (d) is the correct alternative.
Let f : (0, 1) → R be defined by 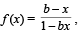 where b is a constant such that 0 < b < 1. Then
where b is a constant such that 0 < b < 1. Then- a)f is not invertible on (0, 1)
- b)
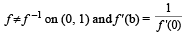
- c)
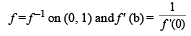
- d)f –1 is differentiable (0, 1)
Correct answer is option 'A,B'. Can you explain this answer?
Let f : (0, 1) → R be defined by 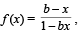 where b is a constant such that 0 < b < 1. Then
where b is a constant such that 0 < b < 1. Then
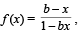 where b is a constant such that 0 < b < 1. Then
where b is a constant such that 0 < b < 1. Thena)
f is not invertible on (0, 1)
b)
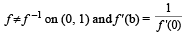
c)
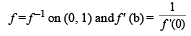
d)
f –1 is differentiable (0, 1)
|
|
Keerthana Bose answered |
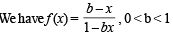
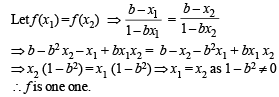
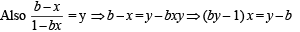
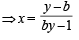
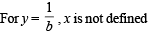
∴ f is neither onto nor invertible
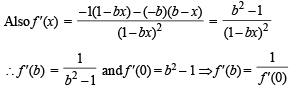
Hence a and b are the correct options.
Let f(x) be defined for all x > 0 and be continuous. Let f(x) 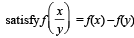 for all x, y and f(e) = 1. Then
for all x, y and f(e) = 1. Then- a)f(x) is bounded
- b)
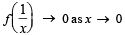
- c)x f(x) → 1 as x → 0
- d)f(x) = ln x
Correct answer is option 'D'. Can you explain this answer?
Let f(x) be defined for all x > 0 and be continuous. Let f(x) 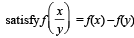 for all x, y and f(e) = 1. Then
for all x, y and f(e) = 1. Then
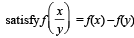 for all x, y and f(e) = 1. Then
for all x, y and f(e) = 1. Thena)
f(x) is bounded
b)
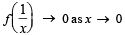
c)
x f(x) → 1 as x → 0
d)
f(x) = ln x
|
|
Siddharth Basak answered |
f (x) is continuous and defined for all x > 0 and

⇒ Clearly f (x) = ln x which satisfies all these properties
∴ f (x) = ℓnx
Chapter doubts & questions for Functions - 35 Years Chapter wise Previous Year Solved Papers for JEE 2025 is part of JEE exam preparation. The chapters have been prepared according to the JEE exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for JEE 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Functions - 35 Years Chapter wise Previous Year Solved Papers for JEE in English & Hindi are available as part of JEE exam.
Download more important topics, notes, lectures and mock test series for JEE Exam by signing up for free.
35 Years Chapter wise Previous Year Solved Papers for JEE
347 docs|185 tests
|
Related JEE Content
Signup to see your scores go up within 7 days!
Study with 1000+ FREE Docs, Videos & Tests
10M+ students study on EduRev

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Forgot Password
OR
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily




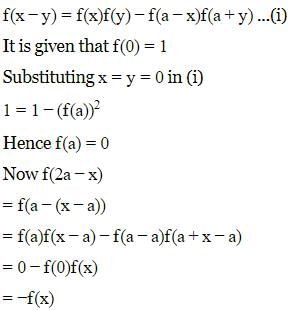
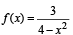
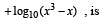

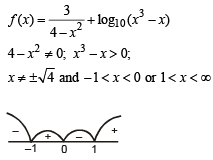
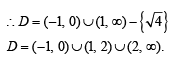

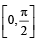
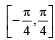
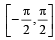
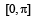

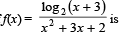

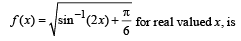
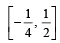
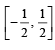
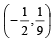
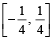
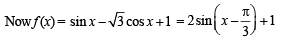
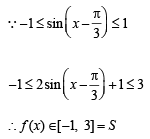


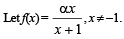 Then, for what value of a is f (f(x)) = x ?
Then, for what value of a is f (f(x)) = x ?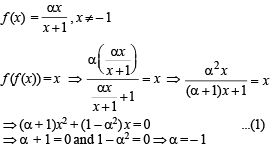
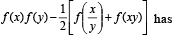 the value
the value
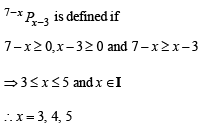
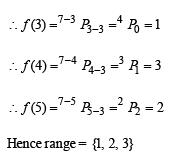
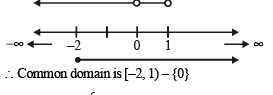
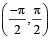 for which the function,
for which the function, 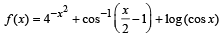 , is defined, is
, is defined, is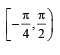
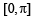
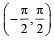
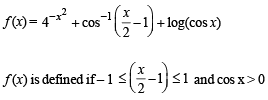
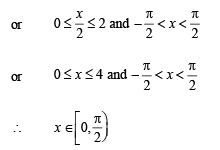
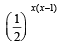
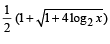
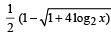

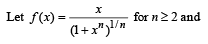
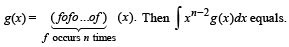
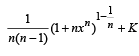
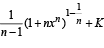
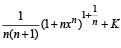
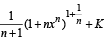

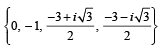
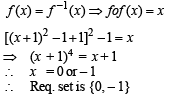
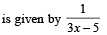
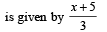

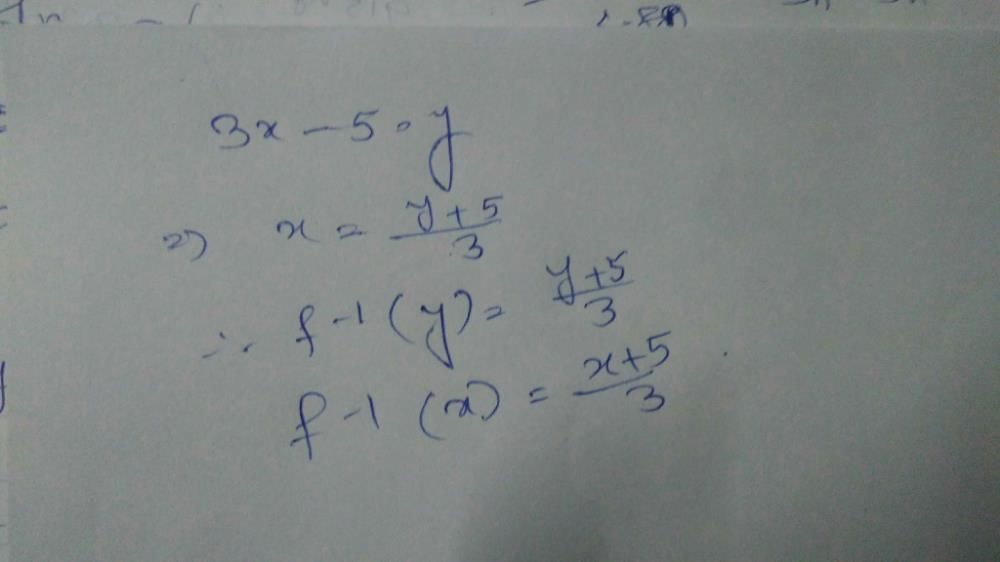
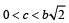
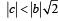
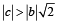
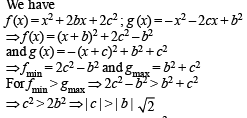
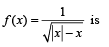

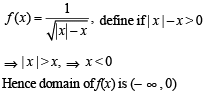
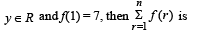
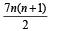
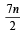
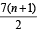
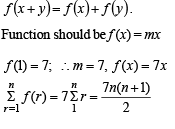
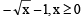
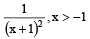
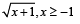
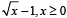
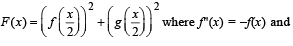 g(x) = f '(x) and given that F(5) = 5, then F(10) is equal to
g(x) = f '(x) and given that F(5) = 5, then F(10) is equal to