All Exams >
JEE >
35 Years Chapter wise Previous Year Solved Papers for JEE >
All Questions
All questions of Vector Algebra and Three Dimensional Geometry for JEE Exam
Let α, β, γ be distinct real numbers. The points with position vectors 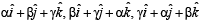
- a)are collinear
- b)form an equilateral triangle
- c)form a scalene triangle
- d)form a right angled triangle
Correct answer is option 'B'. Can you explain this answer?
Let α, β, γ be distinct real numbers. The points with position vectors 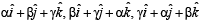
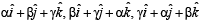
a)
are collinear
b)
form an equilateral triangle
c)
form a scalene triangle
d)
form a right angled triangle
|
|
Anaya Patel answered |
Let the given position vectors be of point A, B and C respectively, then
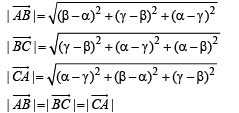
⇒ ΔABC is an equilateral Δ.
If the vectors 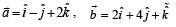 and
and 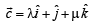 are mutually orthogonal, then (λ, μ)=
are mutually orthogonal, then (λ, μ)=- a)(2, –3)
- b)(–2, 3)
- c)(3, –2)
- d)(–3, 2)
Correct answer is option 'D'. Can you explain this answer?
If the vectors 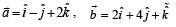 and
and 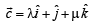 are mutually orthogonal, then (λ, μ)=
are mutually orthogonal, then (λ, μ)=
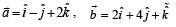 and
and 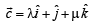 are mutually orthogonal, then (λ, μ)=
are mutually orthogonal, then (λ, μ)=a)
(2, –3)
b)
(–2, 3)
c)
(3, –2)
d)
(–3, 2)
|
|
Anaya Patel answered |
Since 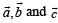 are mutually orthogonal
are mutually orthogonal
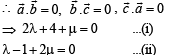
On solving (i) and (ii), we get λ = -3, μ = 2
 are mutually orthogonal
are mutually orthogonal 
On solving (i) and (ii), we get λ = -3, μ = 2
Distance between two parallel planes 2x + y + 2z = 8 and 4x + 2y + 4z + 5 = 0 is- a)3/2
- b)5/2
- c)7/2
- d)9/2
Correct answer is option 'C'. Can you explain this answer?
Distance between two parallel planes 2x + y + 2z = 8 and 4x + 2y + 4z + 5 = 0 is
a)
3/2
b)
5/2
c)
7/2
d)
9/2
|
|
Lavanya Menon answered |
2x + y + 2z – 8 = 0 …(Plane 1)
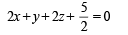 …(Plane 2)
…(Plane 2)Distance between Plane 1 and 2

A tetrahedron has vertices at O(0, 0, 0), A(1, 2, 1) B(2, 1, 3) and C(–1, 1, 2). Then the angle between the faces OAB and ABC will be- a)90°
- b)
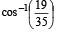
- c)
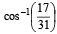
- d)30°
Correct answer is option 'B'. Can you explain this answer?
A tetrahedron has vertices at O(0, 0, 0), A(1, 2, 1) B(2, 1, 3) and C(–1, 1, 2). Then the angle between the faces OAB and ABC will be
a)
90°
b)
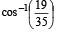
c)
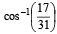
d)
30°
|
|
Lavanya Menon answered |
Vector perpendicular to the face OAB

Vector perpendicular to the face ABC
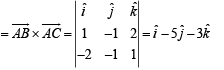
Angle between the faces = angle between their normals
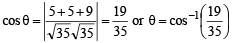
If (2, 3, 5) is one end of a diameter of the sphere x2 + y2 + z2 – 6x – 12y – 2z + 20 = 0, then the cooordinates of the other end of the diameter are- a)(4, 3, 5)
- b)(4, 3, – 3)
- c)(4, 9, – 3)
- d)(4, –3, 3).
Correct answer is option 'C'. Can you explain this answer?
If (2, 3, 5) is one end of a diameter of the sphere x2 + y2 + z2 – 6x – 12y – 2z + 20 = 0, then the cooordinates of the other end of the diameter are
a)
(4, 3, 5)
b)
(4, 3, – 3)
c)
(4, 9, – 3)
d)
(4, –3, 3).
|
|
Ram Mohith answered |
The center for the givens sphere is (3,6,1) and one end of diameter is (2,3,5). So, we can find the other end using mid-point formula. Let the other end be (x,y,z) then,
3 = (2 + x)/2 => x = 4
6 = (3 + y)/2 => y = 9
1 = (5 + z)/2 => z = -3
Therefore, the other end of the diameter is (4,9,-3)
Two system of rectangular axes have the same origin. If a plane cuts them at distances a, b, c and a' , b' , c' from the origin then- a)
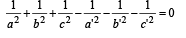
- b)
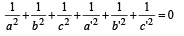
- c)

- d)
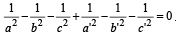
Correct answer is option 'A'. Can you explain this answer?
Two system of rectangular axes have the same origin. If a plane cuts them at distances a, b, c and a' , b' , c' from the origin then
a)
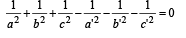
b)
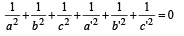
c)

d)
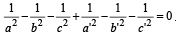
|
|
Chirag Verma answered |
Eq. of planes be 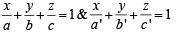
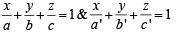
(⊥ r distance on plane from origin is same.)

If the vectors 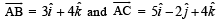 are the sides of a triangle ABC, then the length of the median through A is
are the sides of a triangle ABC, then the length of the median through A is- a)
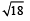
- b)
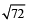
- c)

- d)
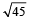
Correct answer is option 'C'. Can you explain this answer?
If the vectors 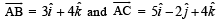 are the sides of a triangle ABC, then the length of the median through A is
are the sides of a triangle ABC, then the length of the median through A is
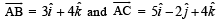 are the sides of a triangle ABC, then the length of the median through A is
are the sides of a triangle ABC, then the length of the median through A isa)
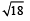
b)
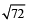
c)

d)
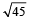
|
|
Chirag Verma answered |
∵ M is mid point of BC
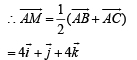
Length of median AM
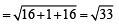
If the line, 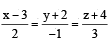 lies in the plane, lx + my – z = 9,then l2 + m2 is equal to :
lies in the plane, lx + my – z = 9,then l2 + m2 is equal to :- a)5
- b)2
- c)26
- d)18
Correct answer is option 'B'. Can you explain this answer?
If the line, 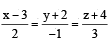 lies in the plane, lx + my – z = 9,then l2 + m2 is equal to :
lies in the plane, lx + my – z = 9,then l2 + m2 is equal to :
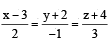 lies in the plane, lx + my – z = 9,then l2 + m2 is equal to :
lies in the plane, lx + my – z = 9,then l2 + m2 is equal to :a)
5
b)
2
c)
26
d)
18
|
|
Rohit Jain answered |
Line lies in the plane ⇒ (3, –2, –4) lie in the plane
⇒ 3ℓ – 2m + 4 = 9 or 3ℓ – 2m = 5 ..... (1)
Also, ℓ, m,–1 are dr's of line perpendicular to plane and 2, –1, 3 are dr's of line lying in the plane
⇒ 2ℓ – m – 3 = 0 or 2ℓ – m = 3 .....(2)
Solving (1) and (2) we get ℓ = 1 and m = –1
⇒ ℓ2 + m2 = 2
⇒ 3ℓ – 2m + 4 = 9 or 3ℓ – 2m = 5 ..... (1)
Also, ℓ, m,–1 are dr's of line perpendicular to plane and 2, –1, 3 are dr's of line lying in the plane
⇒ 2ℓ – m – 3 = 0 or 2ℓ – m = 3 .....(2)
Solving (1) and (2) we get ℓ = 1 and m = –1
⇒ ℓ2 + m2 = 2
Let 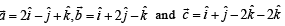 be three vectors. A vector in the plane of
be three vectors. A vector in the plane of 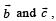 whose projection on
whose projection on 
- a)
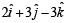
- b)
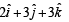
- c)
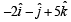
- d)
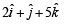
Correct answer is option 'A,C'. Can you explain this answer?
Let 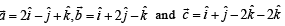 be three vectors. A vector in the plane of
be three vectors. A vector in the plane of 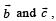 whose projection on
whose projection on 
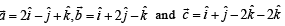 be three vectors. A vector in the plane of
be three vectors. A vector in the plane of 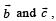 whose projection on
whose projection on 
a)
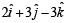
b)
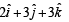
c)
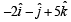
d)
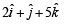
|
|
Chirag Verma answered |
We have

Given magnitude of projection of
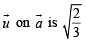
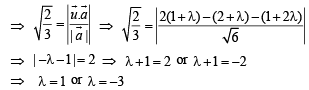
∴ The required vector is either,
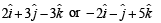
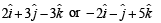
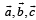 are 3 vectors, such that
are 3 vectors, such that 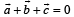
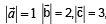 , then
, then 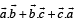 is equal to
is equal to- a)1
- b)0
- c)–7
- d)7
Correct answer is option 'C'. Can you explain this answer?
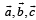 are 3 vectors, such that
are 3 vectors, such that 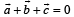
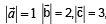 , then
, then 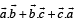 is equal to
is equal toa)
1
b)
0
c)
–7
d)
7

|
Vikash Yadav answered |
Square a+b+c=0
(a+b+c)^2 = a^2 + b^2 + c^2 + 2 a.b + 2 b.c + 2 c.a
0 = 1 + 4 + 9 + 2(a.b + b.c + c.a)
(a.b + b.c + c.a)= -14/2 = -7
If a line makes an angle of π /4 with the positive directions of each of x- axis and y- axis, then the angle that the line makes with the positive direction of the z-axis is- a)π /4
- b)π /2
- c)π /6
- d)π /3
Correct answer is option 'B'. Can you explain this answer?
If a line makes an angle of π /4 with the positive directions of each of x- axis and y- axis, then the angle that the line makes with the positive direction of the z-axis is
a)
π /4
b)
π /2
c)
π /6
d)
π /3
|
|
Tushar Choudhury answered |
Let the angle of line makes with the positive direction of z-axis is a direction cosines of line with the +ve directions of x-axis, y-axis, and z-axis is l, m, n respectively.
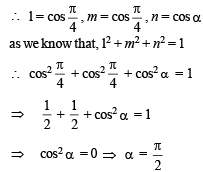
Hence, angle with positive direction of the
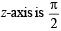
The angle between the lines whose direction cosines satisfy the equations l + m +n= 0 and l2 = m2 + n2 is- a)π/6
- b)π/2
- c)π/3
- d)π/4
Correct answer is option 'C'. Can you explain this answer?
The angle between the lines whose direction cosines satisfy the equations l + m +n= 0 and l2 = m2 + n2 is
a)
π/6
b)
π/2
c)
π/3
d)
π/4
|
|
Nabanita Nambiar answered |
Given l + m + n = 0 and l2 = m2 + n2
Now, (–m –n)2 = m2 + n2
⇒ mn = 0 ⇒ m = 0 or n = 0
If m = 0 then l = –n
Now, (–m –n)2 = m2 + n2
⇒ mn = 0 ⇒ m = 0 or n = 0
If m = 0 then l = –n
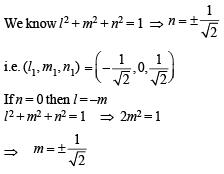
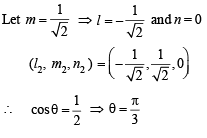
The value of k such that 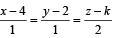 lies in the plane 2x – 4y + z = 7, is
lies in the plane 2x – 4y + z = 7, is- a)7
- b)–7
- c)no real value
- d)4
Correct answer is option 'A'. Can you explain this answer?
The value of k such that 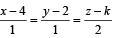 lies in the plane 2x – 4y + z = 7, is
lies in the plane 2x – 4y + z = 7, is
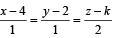 lies in the plane 2x – 4y + z = 7, is
lies in the plane 2x – 4y + z = 7, isa)
7
b)
–7
c)
no real value
d)
4
|
|
Gaurav Kumar answered |
As the line 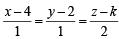 lies in th e plan e 2x - 4 y +z= 7, the point (4, 2, k) through which line passes must also lie on the given plane and hence 2 × 4 – 4 × 2 + k = 7 ⇒ k = 7
lies in th e plan e 2x - 4 y +z= 7, the point (4, 2, k) through which line passes must also lie on the given plane and hence 2 × 4 – 4 × 2 + k = 7 ⇒ k = 7
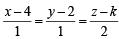 lies in th e plan e 2x - 4 y +z= 7, the point (4, 2, k) through which line passes must also lie on the given plane and hence 2 × 4 – 4 × 2 + k = 7 ⇒ k = 7
lies in th e plan e 2x - 4 y +z= 7, the point (4, 2, k) through which line passes must also lie on the given plane and hence 2 × 4 – 4 × 2 + k = 7 ⇒ k = 7The two lines x = ay+b , z = cy+d ; and x = a' y+b' , z = c' y+d' are perpendicular to each other if- a)aa '+ cc ' =-1
- b)aa '+ cc '=1
- c)
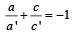
- d)
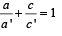
Correct answer is option 'A'. Can you explain this answer?
The two lines x = ay+b , z = cy+d ; and x = a' y+b' , z = c' y+d' are perpendicular to each other if
a)
aa '+ cc ' =-1
b)
aa '+ cc '=1
c)
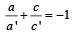
d)
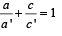
|
|
Harsh Singhal answered |
First find direction of two line by taking cross product of their eq.of plane & then their dot product become zero
Let the line  lie in the plane x + 3y – αz + β = 0. Then (α, β) equals
lie in the plane x + 3y – αz + β = 0. Then (α, β) equals- a)(–6, 7)
- b)(5, –15)
- c)(–5, 5)
- d)(6, –17)
Correct answer is option 'A'. Can you explain this answer?
Let the line  lie in the plane x + 3y – αz + β = 0. Then (α, β) equals
lie in the plane x + 3y – αz + β = 0. Then (α, β) equals
 lie in the plane x + 3y – αz + β = 0. Then (α, β) equals
lie in the plane x + 3y – αz + β = 0. Then (α, β) equalsa)
(–6, 7)
b)
(5, –15)
c)
(–5, 5)
d)
(6, –17)
|
|
Sonu Kumar answered |
Line lie in the plane and line passes through (2, 1,-2) then plane also passes through this point.
by satisfying find relation between alpha and beta.
and second direction ratio of line and plane are perpendicular then by dot products we get the value of alpha.
by satisfying find relation between alpha and beta.
and second direction ratio of line and plane are perpendicular then by dot products we get the value of alpha.
Let 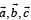 be unit vectors such that
be unit vectors such that  Which one of the following is correct ?
Which one of the following is correct ?- a)
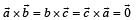
- b)
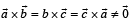
- c)
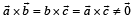
- d)
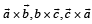 are muturally perpendicular
are muturally perpendicular
Correct answer is option 'B'. Can you explain this answer?
Let 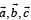 be unit vectors such that
be unit vectors such that  Which one of the following is correct ?
Which one of the following is correct ?
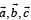 be unit vectors such that
be unit vectors such that  Which one of the following is correct ?
Which one of the following is correct ?a)
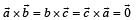
b)
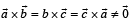
c)
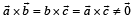
d)
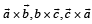 are muturally perpendicular
are muturally perpendicular

|
Ankita Das answered |
These vectors are forming an equilateral triangle so option b will be correct
A line with positive direction cosines passes through the point P(2, –1, 2) and makes equal angles with the coordinate axes. The line meets the plane 2x + y + z = 9 at point Q. The length of the line segment PQ equals- a)1
- b)√2
- c)√3
- d)2
Correct answer is option 'C'. Can you explain this answer?
A line with positive direction cosines passes through the point P(2, –1, 2) and makes equal angles with the coordinate axes. The line meets the plane 2x + y + z = 9 at point Q. The length of the line segment PQ equals
a)
1
b)
√2
c)
√3
d)
2
|
|
Samarth Saha answered |
The line has +ve and equal direction cosines, these are 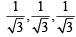 or direction ratios are 1, 1, 1. Also thelines passes through P (2, – 1, 2).
or direction ratios are 1, 1, 1. Also thelines passes through P (2, – 1, 2).
∴ Equation of line is
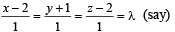
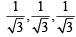 or direction ratios are 1, 1, 1. Also thelines passes through P (2, – 1, 2).
or direction ratios are 1, 1, 1. Also thelines passes through P (2, – 1, 2).∴ Equation of line is
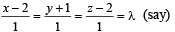
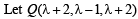 be a point on this line where it meets the plane 2 x + y + z = 9
be a point on this line where it meets the plane 2 x + y + z = 9Then Q must satisfy the eqn of plane
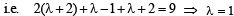
∴ Q has coordintes (3, 0, 3)


Let  If the vectors
If the vectors 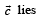 in the plane of
in the plane of 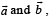 then x equals
then x equals- a)– 4
- b)– 2
- c)0
- d)1.
Correct answer is option 'B'. Can you explain this answer?
Let  If the vectors
If the vectors 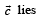 in the plane of
in the plane of 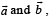 then x equals
then x equals
 If the vectors
If the vectors 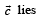 in the plane of
in the plane of 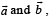 then x equals
then x equalsa)
– 4
b)
– 2
c)
0
d)
1.
|
|
Anand Kumar answered |
Since, vector a,b and c are coplanar.
Therefore, by condition of coplanarity,
vector c=m(vector a)+n(vector b)
substitute the given values of the individual vector.
further, relate coefficient of i,j and k of LHS to RHS
there is will have three relations between X,m and n . solve further for m,n and X.
Therefore, by condition of coplanarity,
vector c=m(vector a)+n(vector b)
substitute the given values of the individual vector.
further, relate coefficient of i,j and k of LHS to RHS
there is will have three relations between X,m and n . solve further for m,n and X.
If 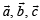 are non-coplanar vectors and l is a real number, then the vectors
are non-coplanar vectors and l is a real number, then the vectors 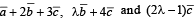 are non coplanar for
are non coplanar for- a)no value of λ
- b)all except on e value of λ
- c)all except two values of λ
- d)all values of λ
Correct answer is option 'C'. Can you explain this answer?
If 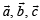 are non-coplanar vectors and l is a real number, then the vectors
are non-coplanar vectors and l is a real number, then the vectors 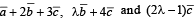 are non coplanar for
are non coplanar for
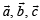 are non-coplanar vectors and l is a real number, then the vectors
are non-coplanar vectors and l is a real number, then the vectors 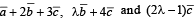 are non coplanar for
are non coplanar fora)
no value of λ
b)
all except on e value of λ
c)
all except two values of λ
d)
all values of λ
|
|
Sahil Ghosh answered |

coplanar if
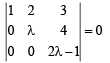

∵ Forces are noncoplanar for all λ, except 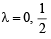
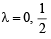
Distance between two parallel planes 2x + y + 2z = 8 and 4x + 2y +4z + 5 = 0 is- a)9/2
- b)5/2
- c)7/2
- d)3/2
Correct answer is option 'C'. Can you explain this answer?
Distance between two parallel planes 2x + y + 2z = 8 and 4x + 2y +4z + 5 = 0 is
a)
9/2
b)
5/2
c)
7/2
d)
3/2
|
|
Kiran Sengupta answered |
To find the distance between two parallel planes, we need to find the perpendicular distance between them. The normal vectors of the planes will be parallel, so we can find the distance between the planes by finding the distance between a point on one plane and the other plane.
Given planes:
1) 2x + y + 2z = 8
2) 4x + 2y + 4z + 5 = 0
Step 1: Find the normal vectors of the planes
The normal vector of a plane is the coefficients of x, y, and z in the equation of the plane. So, the normal vectors for the given planes are:
1) Plane 1: (2, 1, 2)
2) Plane 2: (4, 2, 4)
Step 2: Find a point on one of the planes
To find a point on Plane 1, we can assume a value for one of the variables and solve for the other two variables. Let's assume x = 0. Substituting x = 0 in Plane 1 equation, we get:
y + 2z = 8
Assuming y = 0, we get:
2z = 8
z = 4
So, a point on Plane 1 is (0, 0, 4).
Step 3: Find the distance between the point and Plane 2
To find the distance between a point and a plane, we can use the formula:
Distance = |ax + by + cz + d| / √(a^2 + b^2 + c^2)
where (a, b, c) are the coefficients of x, y, and z in the equation of the plane, and d is the constant term.
Substituting the values for Plane 2, we get:
Distance = |4(0) + 2(0) + 4(4) + 5| / √(4^2 + 2^2 + 4^2)
= |16 + 5| / √(16 + 4 + 16)
= |21| / √(36)
= 21 / 6
= 7/2
Therefore, the distance between the two parallel planes is 7/2, which corresponds to option C.
Given planes:
1) 2x + y + 2z = 8
2) 4x + 2y + 4z + 5 = 0
Step 1: Find the normal vectors of the planes
The normal vector of a plane is the coefficients of x, y, and z in the equation of the plane. So, the normal vectors for the given planes are:
1) Plane 1: (2, 1, 2)
2) Plane 2: (4, 2, 4)
Step 2: Find a point on one of the planes
To find a point on Plane 1, we can assume a value for one of the variables and solve for the other two variables. Let's assume x = 0. Substituting x = 0 in Plane 1 equation, we get:
y + 2z = 8
Assuming y = 0, we get:
2z = 8
z = 4
So, a point on Plane 1 is (0, 0, 4).
Step 3: Find the distance between the point and Plane 2
To find the distance between a point and a plane, we can use the formula:
Distance = |ax + by + cz + d| / √(a^2 + b^2 + c^2)
where (a, b, c) are the coefficients of x, y, and z in the equation of the plane, and d is the constant term.
Substituting the values for Plane 2, we get:
Distance = |4(0) + 2(0) + 4(4) + 5| / √(4^2 + 2^2 + 4^2)
= |16 + 5| / √(16 + 4 + 16)
= |21| / √(36)
= 21 / 6
= 7/2
Therefore, the distance between the two parallel planes is 7/2, which corresponds to option C.
If 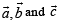 are unit vectors, then
are unit vectors, then 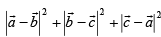 does NOT exceed
does NOT exceed- a)4
- b)9
- c)8
- d)6
Correct answer is option 'B'. Can you explain this answer?
If 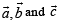 are unit vectors, then
are unit vectors, then 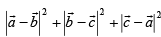 does NOT exceed
does NOT exceed
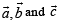 are unit vectors, then
are unit vectors, then 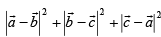 does NOT exceed
does NOT exceeda)
4
b)
9
c)
8
d)
6

|
Ankita Das answered |
Ur ans will be 9 because when angle between a,b,c is 120 it will be maximize
Let 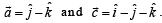 Then the vector
Then the vector 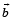 satisfying
satisfying 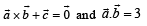
- a)
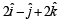
- b)

- c)
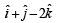
- d)
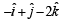
Correct answer is option 'D'. Can you explain this answer?
Let 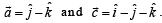 Then the vector
Then the vector 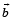 satisfying
satisfying 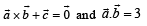
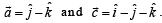 Then the vector
Then the vector 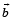 satisfying
satisfying 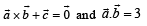
a)
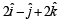
b)

c)
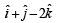
d)
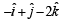
|
|
Sanchita Chavan answered |
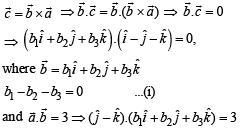

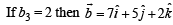 which is not possible
which is not possible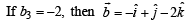
Let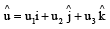 be a unit vector in R3 and
be a unit vector in R3 and 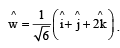 Given that there exists a vector
Given that there exists a vector 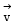 in
in 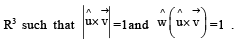 Which of the following statement(s) is (are) correct?
Which of the following statement(s) is (are) correct?- a)There is exactly one choice for such
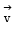
- b)There are in finitely many choices for such
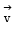
- c)If
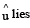 in the xy-plane then |u1| = |u2|
in the xy-plane then |u1| = |u2| - d)If
 in the xz-plane then 2 |u1| = |u3|
in the xz-plane then 2 |u1| = |u3|
Correct answer is option 'B,C'. Can you explain this answer?
Let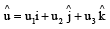 be a unit vector in R3 and
be a unit vector in R3 and 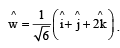 Given that there exists a vector
Given that there exists a vector 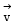 in
in 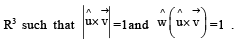 Which of the following statement(s) is (are) correct?
Which of the following statement(s) is (are) correct?
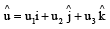 be a unit vector in R3 and
be a unit vector in R3 and 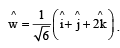 Given that there exists a vector
Given that there exists a vector 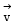 in
in 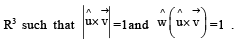 Which of the following statement(s) is (are) correct?
Which of the following statement(s) is (are) correct?a)
There is exactly one choice for such 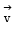
b)
There are in finitely many choices for such 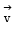
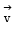
c)
If 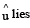 in the xy-plane then |u1| = |u2|
in the xy-plane then |u1| = |u2|
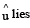 in the xy-plane then |u1| = |u2|
in the xy-plane then |u1| = |u2|d)
If  in the xz-plane then 2 |u1| = |u3|
in the xz-plane then 2 |u1| = |u3|
 in the xz-plane then 2 |u1| = |u3|
in the xz-plane then 2 |u1| = |u3||
|
Ameya Sengupta answered |
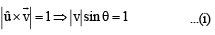
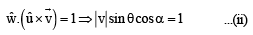
where α is the angle between
From (i) and (ii) cos α = 1 ⇒ a = 0°
 is perpendicular to the plane containing
is perpendicular to the plane containing 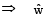 is perpendicular to
is perpendicular to 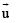
Clearly there can be infinite many choices for 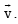

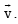

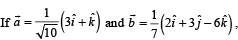 then the value
then the value 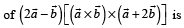
- a)–3
- b)5
- c)3
- d)–5
Correct answer is option 'D'. Can you explain this answer?
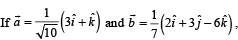 then the value
then the value 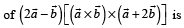
a)
–3
b)
5
c)
3
d)
–5

|
Vikash Yadav answered |
Use vector triple product
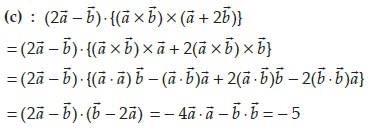
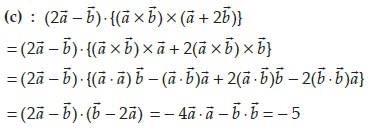
Chapter doubts & questions for Vector Algebra and Three Dimensional Geometry - 35 Years Chapter wise Previous Year Solved Papers for JEE 2025 is part of JEE exam preparation. The chapters have been prepared according to the JEE exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for JEE 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Vector Algebra and Three Dimensional Geometry - 35 Years Chapter wise Previous Year Solved Papers for JEE in English & Hindi are available as part of JEE exam.
Download more important topics, notes, lectures and mock test series for JEE Exam by signing up for free.
35 Years Chapter wise Previous Year Solved Papers for JEE
347 docs|185 tests
|
Related JEE Content
Signup to see your scores go up within 7 days!
Study with 1000+ FREE Docs, Videos & Tests
10M+ students study on EduRev

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Forgot Password
OR
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup



 in (1), we get
in (1), we get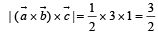
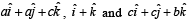 lie in a plane, then c is
lie in a plane, then c is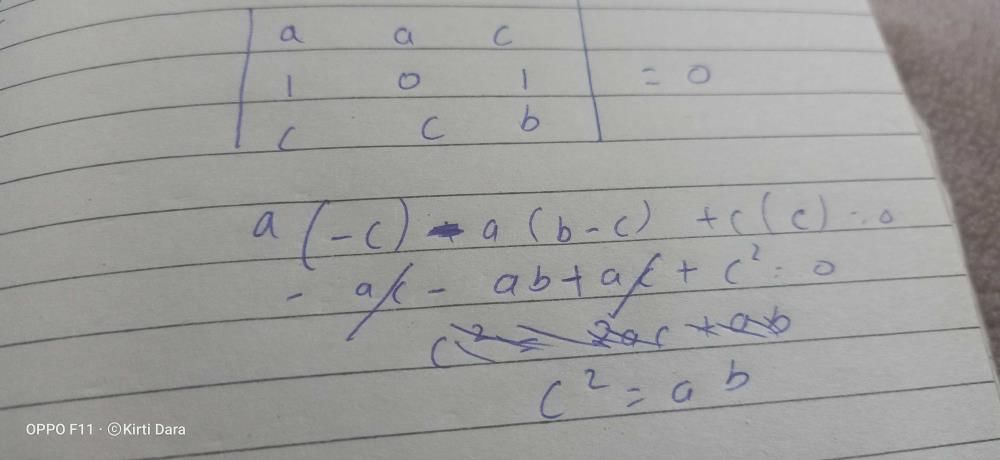
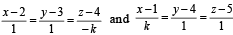 arecoplanar if
arecoplanar if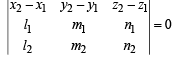
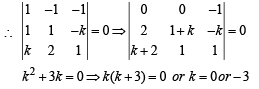
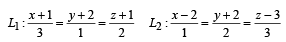
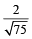
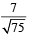
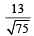
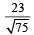

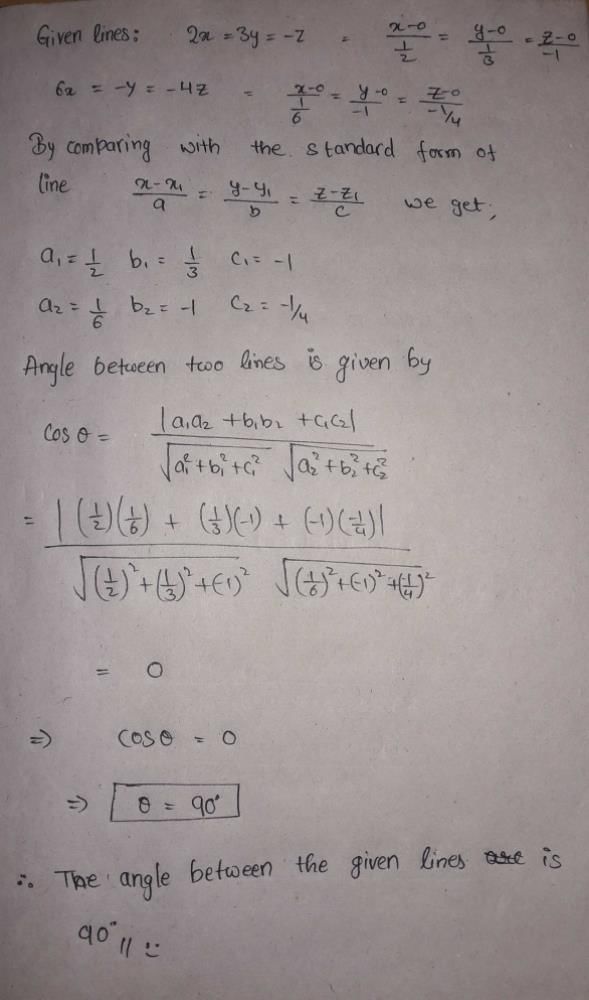
 are coplanar, is
are coplanar, is
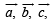 be three non - coplanar vectors and
be three non - coplanar vectors and 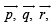 are vectors defined by the relations
are vectors defined by the relations 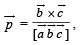
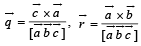 then the value of the expression
then the value of the expression  is equal to
is equal to
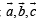 are non coplanar
are non coplanar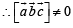
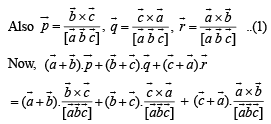
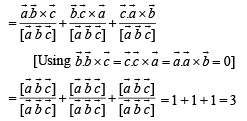
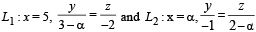 are coplanar. Then a can take value(s)
are coplanar. Then a can take value(s)

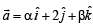 lies in the plane of the vectors
lies in the plane of the vectors 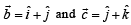 and bisects the angle between
and bisects the angle between 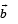
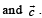 Then which one of the following gives possible values of α and β?
Then which one of the following gives possible values of α and β?

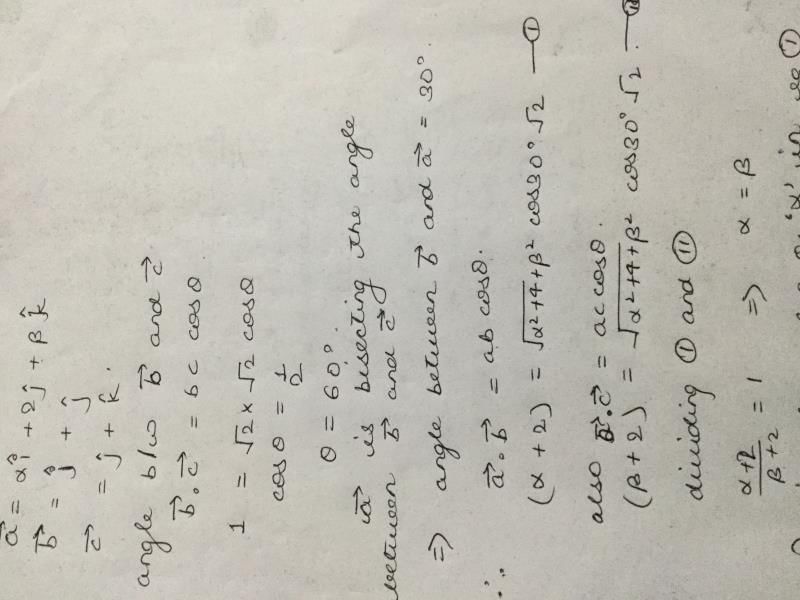
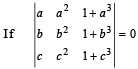 and vectrs (1, a,a2),(1, b, b2) and (1, c,c2) are non- coplanar, then the product abc equals
and vectrs (1, a,a2),(1, b, b2) and (1, c,c2) are non- coplanar, then the product abc equals
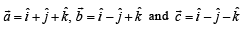 be three vector s. A vector
be three vector s. A vector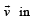 the plane of
the plane of 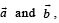 whose projection on
whose projection on 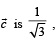 , is given by
, is given by 
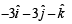
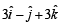
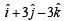
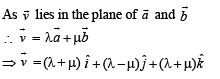
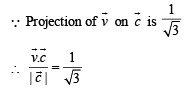
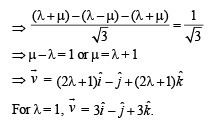

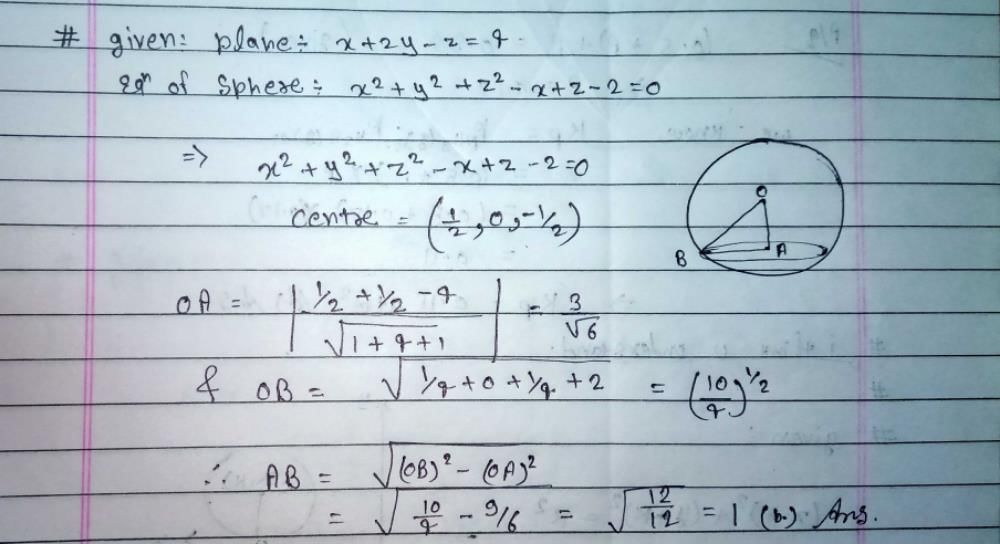
 is a unit vector such that
is a unit vector such that  is equal to
is equal to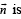 perpendicular
perpendicular 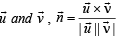
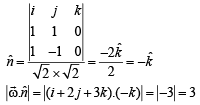
 thus what will be the value of
thus what will be the value of 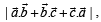 given that
given that 

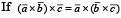 where
where 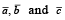 are any three vectors such that
are any three vectors such that 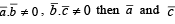 are
are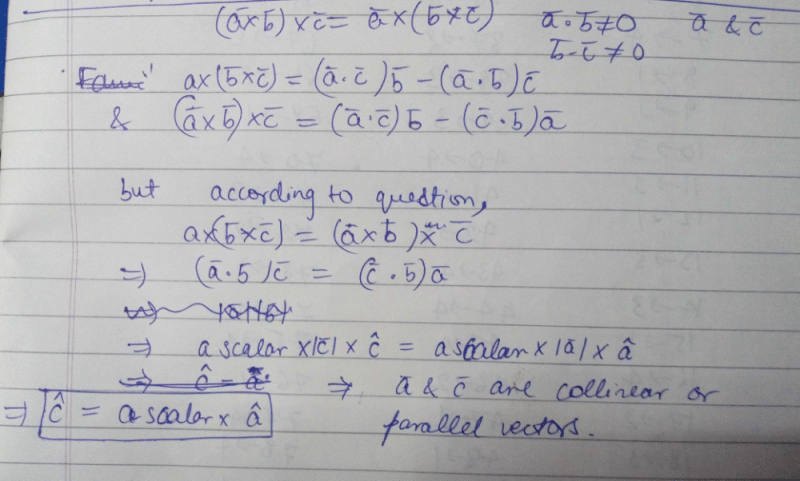
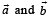 are not perpendicular and
are not perpendicular and 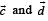 are two vectors satisfying
are two vectors satisfying  Then the vector
Then the vector 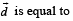
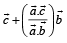

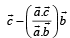
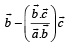
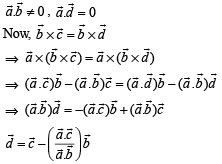
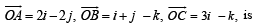

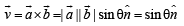
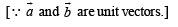
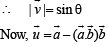
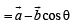
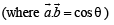

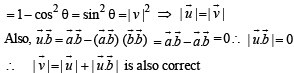
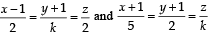 are coplanar, then the plane (s) containing these two lines is (are)
are coplanar, then the plane (s) containing these two lines is (are)
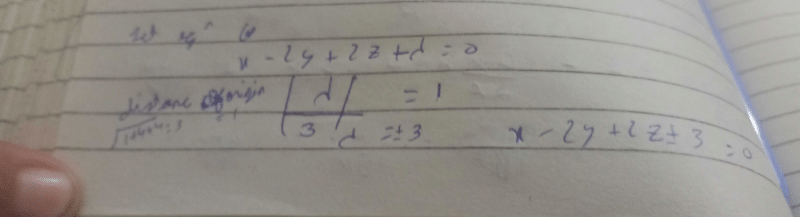
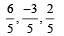
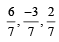
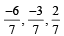

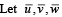 be such that
be such that 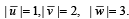 If the projection
If the projection 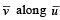 is equal to that of
is equal to that of 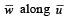 and
and 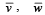 are perpendicular to each other then
are perpendicular to each other then 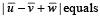
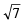
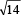

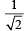
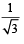
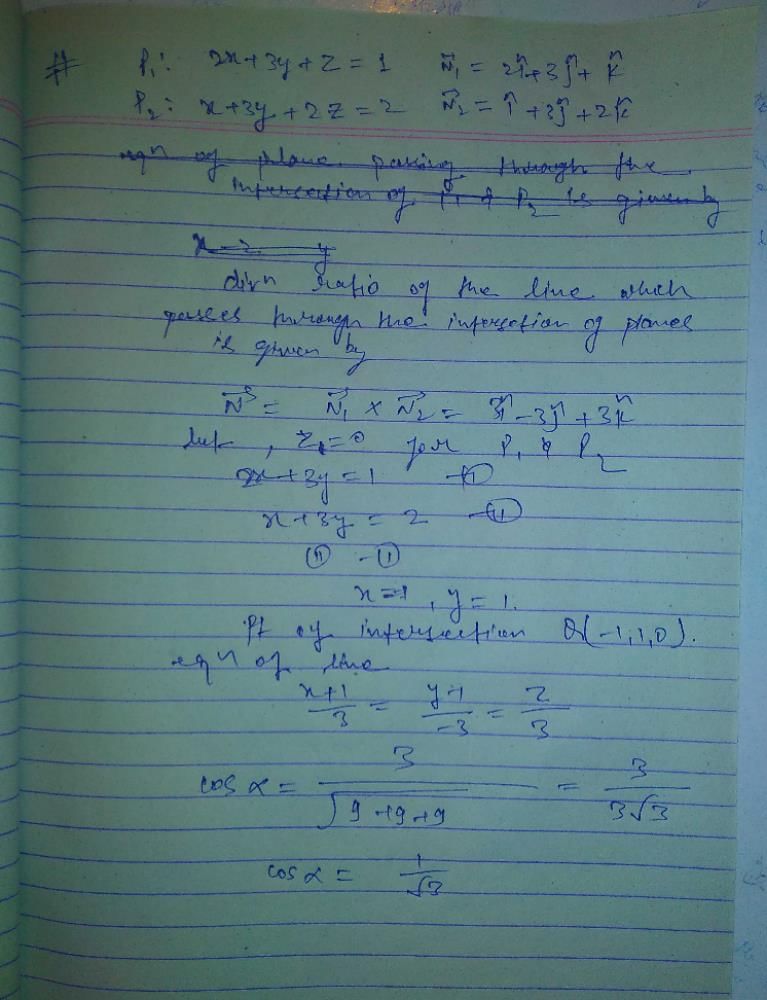
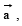 the value of
the value of 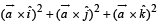 is equal to
is equal to