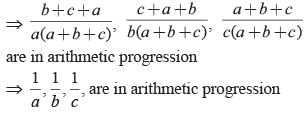All Exams >
Class 10 >
Olympiad Preparation for Class 10 >
All Questions
All questions of Arithmetic Progression for Class 10 Exam
If the sum of n terms of an Arithmetic Progression is given by Sn = 3n2 + 2n. Find its first term and common difference.- a)2, 3
- b)4, 5
- c)5, 6
- d)5, 7
Correct answer is option 'C'. Can you explain this answer?
If the sum of n terms of an Arithmetic Progression is given by Sn = 3n2 + 2n. Find its first term and common difference.
a)
2, 3
b)
4, 5
c)
5, 6
d)
5, 7
|
|
Ritu Saxena answered |
Given Sn = 3n2 + 2n
∴ S1 = 3 × 12 + 2 × 1 = 5
S2 = 3 × 22 + 2 × 2 = 16
The sequence is 5, 11, …..
a = 5 , d = 11 - 5 = 6
∴ S1 = 3 × 12 + 2 × 1 = 5
S2 = 3 × 22 + 2 × 2 = 16
The sequence is 5, 11, …..
a = 5 , d = 11 - 5 = 6
What is the sum of first 30 terms of the arithmetic progression whose 2nd term is 8 and 4th term is 14?- a)1435
- b)1495
- c)1455
- d)1465
Correct answer is option 'C'. Can you explain this answer?
What is the sum of first 30 terms of the arithmetic progression whose 2nd term is 8 and 4th term is 14?
a)
1435
b)
1495
c)
1455
d)
1465
|
|
Samiksha dasgupta answered |
To find the sum of the first 30 terms of an arithmetic progression, we need to know the first term (a) and the common difference (d).
Given information:
- The second term (a2) is 8.
- The fourth term (a4) is 14.
Finding the common difference:
We can find the common difference by subtracting the second term from the first term.
a2 = a + d
8 = a + d
Similarly, we can find the fourth term in terms of the first term and the common difference.
a4 = a + 3d
14 = a + 3d
We now have a system of equations:
a + d = 8
a + 3d = 14
Solving this system of equations, we find:
a = 2
d = 6
Finding the sum of the first 30 terms:
The sum of an arithmetic progression can be found using the formula:
Sn = (n/2)(2a + (n-1)d)
Substituting the values:
S30 = (30/2)(2(2) + (30-1)(6))
S30 = 15(4 + 29(6))
S30 = 15(4 + 174)
S30 = 15(178)
S30 = 2670
Therefore, the sum of the first 30 terms of the arithmetic progression is 2670.
So, the correct answer is option C) 1455.
Given information:
- The second term (a2) is 8.
- The fourth term (a4) is 14.
Finding the common difference:
We can find the common difference by subtracting the second term from the first term.
a2 = a + d
8 = a + d
Similarly, we can find the fourth term in terms of the first term and the common difference.
a4 = a + 3d
14 = a + 3d
We now have a system of equations:
a + d = 8
a + 3d = 14
Solving this system of equations, we find:
a = 2
d = 6
Finding the sum of the first 30 terms:
The sum of an arithmetic progression can be found using the formula:
Sn = (n/2)(2a + (n-1)d)
Substituting the values:
S30 = (30/2)(2(2) + (30-1)(6))
S30 = 15(4 + 29(6))
S30 = 15(4 + 174)
S30 = 15(178)
S30 = 2670
Therefore, the sum of the first 30 terms of the arithmetic progression is 2670.
So, the correct answer is option C) 1455.
What is the value of k for which 5k + 2, 4k - 1 and k + 2 are in arithmetic progression?- a)2
- b)3
- c)4
- d)6
Correct answer is option 'B'. Can you explain this answer?
What is the value of k for which 5k + 2, 4k - 1 and k + 2 are in arithmetic progression?
a)
2
b)
3
c)
4
d)
6
|
|
Vivek Bansal answered |
Here 4k - 1 - (5k + 2) = (k + 2) - (4k - 1)
⇒ 4k - 1 - 5k - 2 = k + 2 - 4k + 1
⇒ -k - 3 = -3k + 3
⇒ 2k = 6 ⇒ k = 3
⇒ 4k - 1 - 5k - 2 = k + 2 - 4k + 1
⇒ -k - 3 = -3k + 3
⇒ 2k = 6 ⇒ k = 3
Raghav buys a shop for ₹ 120000. He pays half of the amount in cash and agrees to pay the balance in 12 annual instalments of ₹ 5000 each. If the rate of interest is 12% and he pays the interest due on the unpaid amount with the instalment. Find the total cost of the shop.- a)₹156800
- b)₹156700
- c)₹165200
- d)₹166800
Correct answer is option 'D'. Can you explain this answer?
Raghav buys a shop for ₹ 120000. He pays half of the amount in cash and agrees to pay the balance in 12 annual instalments of ₹ 5000 each. If the rate of interest is 12% and he pays the interest due on the unpaid amount with the instalment. Find the total cost of the shop.
a)
₹156800
b)
₹156700
c)
₹165200
d)
₹166800
|
|
Anshuman mehra answered |
Given:
Cost of the shop = Rs. 120000
Amount paid in cash = Rs. 60000
Balance amount = Rs. 60000
Rate of interest = 12%
Number of annual instalments = 12
Amount of each instalment = Rs. 5000
To find:
Total cost of the shop
Calculation:
1. Interest on the unpaid amount:
The unpaid amount is Rs. 60000. The interest rate is 12%. So, the interest on the unpaid amount can be calculated using the formula: Interest = (Principal * Rate * Time) / 100
Here, Principal = Rs. 60000, Rate = 12%, and Time = 1 year.
So, the interest = (60000 * 12 * 1) / 100 = Rs. 7200
2. Total amount paid in instalments:
Number of instalments = 12
Amount of each instalment = Rs. 5000
So, the total amount paid in instalments = Number of instalments * Amount of each instalment
= 12 * 5000 = Rs. 60000
3. Total cost of the shop:
The total cost of the shop can be calculated by adding the amount paid in cash, the interest on the unpaid amount, and the total amount paid in instalments.
Total cost of the shop = Amount paid in cash + Interest on unpaid amount + Total amount paid in instalments
= 60000 + 7200 + 60000
= Rs. 127200
Therefore, the total cost of the shop is Rs. 127200, which is not mentioned in the given options.
Cost of the shop = Rs. 120000
Amount paid in cash = Rs. 60000
Balance amount = Rs. 60000
Rate of interest = 12%
Number of annual instalments = 12
Amount of each instalment = Rs. 5000
To find:
Total cost of the shop
Calculation:
1. Interest on the unpaid amount:
The unpaid amount is Rs. 60000. The interest rate is 12%. So, the interest on the unpaid amount can be calculated using the formula: Interest = (Principal * Rate * Time) / 100
Here, Principal = Rs. 60000, Rate = 12%, and Time = 1 year.
So, the interest = (60000 * 12 * 1) / 100 = Rs. 7200
2. Total amount paid in instalments:
Number of instalments = 12
Amount of each instalment = Rs. 5000
So, the total amount paid in instalments = Number of instalments * Amount of each instalment
= 12 * 5000 = Rs. 60000
3. Total cost of the shop:
The total cost of the shop can be calculated by adding the amount paid in cash, the interest on the unpaid amount, and the total amount paid in instalments.
Total cost of the shop = Amount paid in cash + Interest on unpaid amount + Total amount paid in instalments
= 60000 + 7200 + 60000
= Rs. 127200
Therefore, the total cost of the shop is Rs. 127200, which is not mentioned in the given options.
If there are (2n + 1) terms in A.P., then find the ratio of the sum of odd terms and the sum of even terms.- a)n : (n + 1)
- b)(n + 1) : n
- c)n : (n + 2)
- d)(n + 2) : n
Correct answer is option 'B'. Can you explain this answer?
If there are (2n + 1) terms in A.P., then find the ratio of the sum of odd terms and the sum of even terms.
a)
n : (n + 1)
b)
(n + 1) : n
c)
n : (n + 2)
d)
(n + 2) : n
|
|
Ritu Saxena answered |
Let a and d be the first term and common difference respectively of the given A.P.
Now, S1 = Sum of odd terms
⇒ S1 = a1 + a3 + a5 + ...+ a2n+1
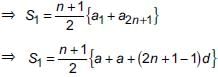
⇒ S1 = (n + 1) (a + nd)
and, S2 = Sum of even terms
⇒ S2 = a2 + a4 + a6 + ... + a2n ⇒ S2 = n/2[a2 + a2n]
⇒ S2 = n/2 [(a+d)+{a+(2n-1)d}]
⇒ S2 = n(a + nd)
∴ S1 : S2 = (n + 1) (a + nd) : n(a + nd) = (n + 1) : n
Now, S1 = Sum of odd terms
⇒ S1 = a1 + a3 + a5 + ...+ a2n+1
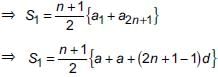
⇒ S1 = (n + 1) (a + nd)
and, S2 = Sum of even terms
⇒ S2 = a2 + a4 + a6 + ... + a2n ⇒ S2 = n/2[a2 + a2n]
⇒ S2 = n/2 [(a+d)+{a+(2n-1)d}]
⇒ S2 = n(a + nd)
∴ S1 : S2 = (n + 1) (a + nd) : n(a + nd) = (n + 1) : n
Deepak repays his total loan of ₹1,18,000 by paying every month starting with the first instalment of ₹1000. If he increases the instalment by ₹100 every month. what amount will be paid as the last instalment of loan?- a)₹4900
- b)₹5400
- c)₹3500
- d)₹4500
Correct answer is option 'A'. Can you explain this answer?
Deepak repays his total loan of ₹1,18,000 by paying every month starting with the first instalment of ₹1000. If he increases the instalment by ₹100 every month. what amount will be paid as the last instalment of loan?
a)
₹4900
b)
₹5400
c)
₹3500
d)
₹4500
|
|
Ritu Saxena answered |
1st instalment = ₹ 1000
2nd instalment = ₹ 1000 + ₹ 100 = ₹ 1100
3rd instalment = ₹ 1100 + ₹ 100 = ₹ 1200 and so on
Let number of instalments = n
∴ 1000 + 1100 + 1200 + ... up to n terms = 118000
⇒ n/2[2x1000+(n-1)100] = 118000
⇒ 100n2 + 1900n – 236000 = 0
⇒ n2 + 19n – 2360 = 0 ⇒ (n + 59)(n – 40) = 0
⇒ n = 40 (∴ n ≠ – 59)
∴ Total no. of instalments = 40
Now, last instalment = 40th instalment
∴ a40 = a + 39d = ₹ 4900
2nd instalment = ₹ 1000 + ₹ 100 = ₹ 1100
3rd instalment = ₹ 1100 + ₹ 100 = ₹ 1200 and so on
Let number of instalments = n
∴ 1000 + 1100 + 1200 + ... up to n terms = 118000
⇒ n/2[2x1000+(n-1)100] = 118000
⇒ 100n2 + 1900n – 236000 = 0
⇒ n2 + 19n – 2360 = 0 ⇒ (n + 59)(n – 40) = 0
⇒ n = 40 (∴ n ≠ – 59)
∴ Total no. of instalments = 40
Now, last instalment = 40th instalment
∴ a40 = a + 39d = ₹ 4900
What is the sum of all three digit natural numbers which are multiples of 7?- a)72336
- b)70336
- c)72036
- d)72396
Correct answer is option 'B'. Can you explain this answer?
What is the sum of all three digit natural numbers which are multiples of 7?
a)
72336
b)
70336
c)
72036
d)
72396

|
Sakshi Chopra answered |
Sum of Three-Digit Numbers Multiples of 7
To find the sum of all three-digit natural numbers which are multiples of 7, we need to determine the first and last numbers in the sequence and then use the formula for the sum of an arithmetic series.
Finding the First and Last Numbers
- The smallest three-digit number that is a multiple of 7 is 105 (7 x 15).
- The largest three-digit number that is a multiple of 7 is 994 (7 x 142).
Calculating the Number of Terms
- To find the number of terms in the sequence, we use the formula:
Number of terms = (Last term - First term) / Common difference + 1
Number of terms = (994 - 105) / 7 + 1
Number of terms = 142 - 15 + 1
Number of terms = 128
Sum of an Arithmetic Series
- The sum of an arithmetic series can be calculated using the formula:
Sum = n/2 * (first term + last term)
Sum = 128/2 * (105 + 994)
Sum = 64 * 1099
Sum = 70336
Therefore, the sum of all three-digit natural numbers which are multiples of 7 is 70336, which corresponds to option 'B'.
To find the sum of all three-digit natural numbers which are multiples of 7, we need to determine the first and last numbers in the sequence and then use the formula for the sum of an arithmetic series.
Finding the First and Last Numbers
- The smallest three-digit number that is a multiple of 7 is 105 (7 x 15).
- The largest three-digit number that is a multiple of 7 is 994 (7 x 142).
Calculating the Number of Terms
- To find the number of terms in the sequence, we use the formula:
Number of terms = (Last term - First term) / Common difference + 1
Number of terms = (994 - 105) / 7 + 1
Number of terms = 142 - 15 + 1
Number of terms = 128
Sum of an Arithmetic Series
- The sum of an arithmetic series can be calculated using the formula:
Sum = n/2 * (first term + last term)
Sum = 128/2 * (105 + 994)
Sum = 64 * 1099
Sum = 70336
Therefore, the sum of all three-digit natural numbers which are multiples of 7 is 70336, which corresponds to option 'B'.
The sum of all terms of the arithmetic progression having ten terms except for the first term, is 99, and except for the sixth term, is 89. Find the 8th term of the progression if the sum of the first and the fifth term is equal to 10.- a)15
- b)25
- c)18
- d)10
Correct answer is option 'A'. Can you explain this answer?
The sum of all terms of the arithmetic progression having ten terms except for the first term, is 99, and except for the sixth term, is 89. Find the 8th term of the progression if the sum of the first and the fifth term is equal to 10.
a)
15
b)
25
c)
18
d)
10
|
|
Meghana choudhary answered |
To solve this problem, we can start by setting up the arithmetic progression. Let's assume the first term is 'a' and the common difference is 'd'.
Setting up the arithmetic progression:
The sum of all terms except the first term is 99. Since there are 10 terms, the sum of the remaining 9 terms can be expressed as (9/2)(2a + (9-1)d) = 99.
The sum of all terms except the sixth term is 89. Since there are 10 terms, the sum of the remaining 9 terms can be expressed as (9/2)(2a + (9-1)d) - (a + 5d) = 89.
Now, let's solve these two equations simultaneously to find the values of 'a' and 'd'.
(9/2)(2a + 8d) = 99 ...(1)
(9/2)(2a + 8d) - (a + 5d) = 89 ...(2)
Simplifying equation (2):
(9/2)(2a + 8d) - (a + 5d) = 89
9(2a + 8d) - 2(a + 5d) = 178
18a + 72d - 2a - 10d = 178
16a + 62d = 178 ...(3)
Substituting equation (1) into equation (3):
16a + 62d = 178
16(99/9) + 62d = 178
(16*11) + 62d = 178
176 + 62d = 178
62d = 178 - 176
62d = 2
d = 2/62
d = 1/31
Now, substitute the value of 'd' into equation (1) to find 'a':
(9/2)(2a + 8(1/31)) = 99
(9/2)(2a + 8/31) = 99
(9/2)(62a + 8)/31 = 99
(558a + 72)/31 = 99
558a + 72 = 99 * 31
558a + 72 = 3069
558a = 3069 - 72
558a = 2997
a = 2997/558
a = 27/5
Now that we know the values of 'a' and 'd', we can find the 8th term of the arithmetic progression.
8th term = a + 7d
8th term = (27/5) + 7(1/31)
8th term = (27/5) + (7/31)
8th term = (27*31 + 5*7)/(5*31)
8th term = (837 + 35)/(155)
8th term = 872/155
8th term = 5.632
Therefore, the 8th term of the arithmetic progression is approximately 5.632.
Setting up the arithmetic progression:
The sum of all terms except the first term is 99. Since there are 10 terms, the sum of the remaining 9 terms can be expressed as (9/2)(2a + (9-1)d) = 99.
The sum of all terms except the sixth term is 89. Since there are 10 terms, the sum of the remaining 9 terms can be expressed as (9/2)(2a + (9-1)d) - (a + 5d) = 89.
Now, let's solve these two equations simultaneously to find the values of 'a' and 'd'.
(9/2)(2a + 8d) = 99 ...(1)
(9/2)(2a + 8d) - (a + 5d) = 89 ...(2)
Simplifying equation (2):
(9/2)(2a + 8d) - (a + 5d) = 89
9(2a + 8d) - 2(a + 5d) = 178
18a + 72d - 2a - 10d = 178
16a + 62d = 178 ...(3)
Substituting equation (1) into equation (3):
16a + 62d = 178
16(99/9) + 62d = 178
(16*11) + 62d = 178
176 + 62d = 178
62d = 178 - 176
62d = 2
d = 2/62
d = 1/31
Now, substitute the value of 'd' into equation (1) to find 'a':
(9/2)(2a + 8(1/31)) = 99
(9/2)(2a + 8/31) = 99
(9/2)(62a + 8)/31 = 99
(558a + 72)/31 = 99
558a + 72 = 99 * 31
558a + 72 = 3069
558a = 3069 - 72
558a = 2997
a = 2997/558
a = 27/5
Now that we know the values of 'a' and 'd', we can find the 8th term of the arithmetic progression.
8th term = a + 7d
8th term = (27/5) + 7(1/31)
8th term = (27/5) + (7/31)
8th term = (27*31 + 5*7)/(5*31)
8th term = (837 + 35)/(155)
8th term = 872/155
8th term = 5.632
Therefore, the 8th term of the arithmetic progression is approximately 5.632.
If 8th term of an arithmetic progression is 31 and its 15th term is 16 more than 11th term of the arithmetic progression. What is the first term of that arithmetic progression?- a)4
- b)3
- c)-4
- d)-3
Correct answer is option 'B'. Can you explain this answer?
If 8th term of an arithmetic progression is 31 and its 15th term is 16 more than 11th term of the arithmetic progression. What is the first term of that arithmetic progression?
a)
4
b)
3
c)
-4
d)
-3
|
|
Ritu Saxena answered |
Let a be the first term and d be the common difference
a + 7d = 31
a + 14d = a + 10d + 16
a + 14d - a - 10d = 16
⇒ d = 4
∴ a = 31 - 7d = 31 - 28 = 3
a + 7d = 31
a + 14d = a + 10d + 16
a + 14d - a - 10d = 16
⇒ d = 4
∴ a = 31 - 7d = 31 - 28 = 3
If the 3rd and 7th terms of an arithmetic progression are 17 and 27 respectively. Find the first term of arithmetic progression.- a)12
- b)14
- c)10
- d)8
Correct answer is option 'A'. Can you explain this answer?
If the 3rd and 7th terms of an arithmetic progression are 17 and 27 respectively. Find the first term of arithmetic progression.
a)
12
b)
14
c)
10
d)
8
|
|
Seema joshi answered |
To find the first term of an arithmetic progression, we need to determine the common difference (d) and use it to find the first term (a₁).
Given information:
- The 3rd term is 17
- The 7th term is 27
Step 1: Find the common difference (d)
The common difference (d) is the difference between any two consecutive terms in an arithmetic progression. We can use the formula for the general term (an) of an arithmetic progression to find the common difference.
The general formula for the nth term (an) of an arithmetic progression is:
an = a₁ + (n - 1)d
We can use this formula with the given information to set up two equations:
17 = a₁ + (3 - 1)d ...(1)
27 = a₁ + (7 - 1)d ...(2)
Step 2: Solve the equations
We now have a system of two equations with two unknowns (a₁ and d). We can solve this system of equations to find the values of a₁ and d.
Subtract equation (1) from equation (2) to eliminate a₁:
27 - 17 = (a₁ + (7 - 1)d) - (a₁ + (3 - 1)d)
10 = a₁ + 6d - a₁ - 2d
10 = 4d
Divide both sides of the equation by 4:
d = 10/4
d = 2.5
Step 3: Find the first term (a₁)
We can substitute the value of d into equation (1) or (2) to find the value of a₁.
Let's use equation (1):
17 = a₁ + (3 - 1)(2.5)
17 = a₁ + 2(2.5)
17 = a₁ + 5
a₁ = 17 - 5
a₁ = 12
Therefore, the first term of the arithmetic progression is 12.
Given information:
- The 3rd term is 17
- The 7th term is 27
Step 1: Find the common difference (d)
The common difference (d) is the difference between any two consecutive terms in an arithmetic progression. We can use the formula for the general term (an) of an arithmetic progression to find the common difference.
The general formula for the nth term (an) of an arithmetic progression is:
an = a₁ + (n - 1)d
We can use this formula with the given information to set up two equations:
17 = a₁ + (3 - 1)d ...(1)
27 = a₁ + (7 - 1)d ...(2)
Step 2: Solve the equations
We now have a system of two equations with two unknowns (a₁ and d). We can solve this system of equations to find the values of a₁ and d.
Subtract equation (1) from equation (2) to eliminate a₁:
27 - 17 = (a₁ + (7 - 1)d) - (a₁ + (3 - 1)d)
10 = a₁ + 6d - a₁ - 2d
10 = 4d
Divide both sides of the equation by 4:
d = 10/4
d = 2.5
Step 3: Find the first term (a₁)
We can substitute the value of d into equation (1) or (2) to find the value of a₁.
Let's use equation (1):
17 = a₁ + (3 - 1)(2.5)
17 = a₁ + 2(2.5)
17 = a₁ + 5
a₁ = 17 - 5
a₁ = 12
Therefore, the first term of the arithmetic progression is 12.
The sum of the three numbers in arithmetic progression is 12. The sum of their cubes is 288. What are the numbers?- a)2, 4, 6
- b)4, 6, 8
- c)6, 8, 10
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
The sum of the three numbers in arithmetic progression is 12. The sum of their cubes is 288. What are the numbers?
a)
2, 4, 6
b)
4, 6, 8
c)
6, 8, 10
d)
None of these
|
|
Ritu Saxena answered |
Let the numbers be a - d, a, a + d.
a - d + a + a + d = 12 ⇒ 3a = 12 ⇒ a = 4
and (a - d)3 + a3 + (a + d)3 = 288
a3 - d3 - 3ad(a - d) + a3 + a3 + d3 + 3ad(a + d) = 288
a3 - d3 - 3ad(a - d) + a3 + a3 + a3 + 3ad + 3ad2 = 288
⇒ 3a3 + 6ad2 = 288 ⇒ 3 × 43 + 6 × 4 × d2 = 288
⇒ 24d2 = 288 - 192
⇒ d2 = 95/24 = 4
⇒ d = ±2
a - d + a + a + d = 12 ⇒ 3a = 12 ⇒ a = 4
and (a - d)3 + a3 + (a + d)3 = 288
a3 - d3 - 3ad(a - d) + a3 + a3 + d3 + 3ad(a + d) = 288
a3 - d3 - 3ad(a - d) + a3 + a3 + a3 + 3ad + 3ad2 = 288
⇒ 3a3 + 6ad2 = 288 ⇒ 3 × 43 + 6 × 4 × d2 = 288
⇒ 24d2 = 288 - 192
⇒ d2 = 95/24 = 4
⇒ d = ±2
The sum of n terms of the three arithmetic progression are S1, S2, S3. The first term of each arithmetic progression is unity. The common differences are 1, 2, 3 respectively, then which of the following options is correct?- a)S1 + S3 = 2S2
- b)S1 - S3 = S2
- c)S1 + S2 = S3
- d)S1 + S3 + = S2
Correct answer is option 'A'. Can you explain this answer?
The sum of n terms of the three arithmetic progression are S1, S2, S3. The first term of each arithmetic progression is unity. The common differences are 1, 2, 3 respectively, then which of the following options is correct?
a)
S1 + S3 = 2S2
b)
S1 - S3 = S2
c)
S1 + S2 = S3
d)
S1 + S3 + = S2
|
|
Ritu Saxena answered |
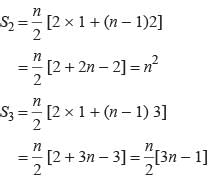

The sum of three numbers in arithmetic is 27 and their product is 405. What are the numbers?- a)3, 9, 15
- b)1, 9, 17
- c)5, 9, 13
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
The sum of three numbers in arithmetic is 27 and their product is 405. What are the numbers?
a)
3, 9, 15
b)
1, 9, 17
c)
5, 9, 13
d)
None of these
|
|
Shiladitya shah answered |
To solve this problem, we need to find three numbers that have the following properties:
1. Their sum is 27.
2. Their product is 405.
Let's assume the three numbers are a, b, and c.
Sum of the numbers:
a + b + c = 27
Product of the numbers:
abc = 405
Now, we need to find the values of a, b, and c that satisfy both of these equations.
Using trial and error method:
We can start by guessing some values and checking if they satisfy both equations.
Let's try option a) 3, 9, 15:
3 + 9 + 15 = 27 (Sum is correct)
3 * 9 * 15 = 405 (Product is correct)
Therefore, option a) 3, 9, 15 satisfies both equations.
Using algebraic method:
We can solve the equations algebraically to find the values of a, b, and c.
From the equation a + b + c = 27, we can rewrite it as c = 27 - a - b.
Substituting this value of c in the equation abc = 405, we get:
ab(27 - a - b) = 405
Expanding the equation:
27ab - a^2b - ab^2 = 405
Rearranging the equation:
a^2b + ab^2 - 27ab + 405 = 0
Now, we can try to factorize this equation:
ab(a + b - 27) + 405 = 0
Since the product of a, b, and (a + b - 27) is positive (405), we can conclude that either:
1. a, b, and (a + b - 27) are all positive, or
2. a, b, and (a + b - 27) are all negative.
If we try different values of a and b that satisfy these conditions, we will find that the only solution is a = 3 and b = 9.
Substituting these values back into the equation c = 27 - a - b, we get c = 15.
Therefore, the numbers are 3, 9, and 15, which matches option a).
Hence, the correct answer is option a) 3, 9, 15.
1. Their sum is 27.
2. Their product is 405.
Let's assume the three numbers are a, b, and c.
Sum of the numbers:
a + b + c = 27
Product of the numbers:
abc = 405
Now, we need to find the values of a, b, and c that satisfy both of these equations.
Using trial and error method:
We can start by guessing some values and checking if they satisfy both equations.
Let's try option a) 3, 9, 15:
3 + 9 + 15 = 27 (Sum is correct)
3 * 9 * 15 = 405 (Product is correct)
Therefore, option a) 3, 9, 15 satisfies both equations.
Using algebraic method:
We can solve the equations algebraically to find the values of a, b, and c.
From the equation a + b + c = 27, we can rewrite it as c = 27 - a - b.
Substituting this value of c in the equation abc = 405, we get:
ab(27 - a - b) = 405
Expanding the equation:
27ab - a^2b - ab^2 = 405
Rearranging the equation:
a^2b + ab^2 - 27ab + 405 = 0
Now, we can try to factorize this equation:
ab(a + b - 27) + 405 = 0
Since the product of a, b, and (a + b - 27) is positive (405), we can conclude that either:
1. a, b, and (a + b - 27) are all positive, or
2. a, b, and (a + b - 27) are all negative.
If we try different values of a and b that satisfy these conditions, we will find that the only solution is a = 3 and b = 9.
Substituting these values back into the equation c = 27 - a - b, we get c = 15.
Therefore, the numbers are 3, 9, and 15, which matches option a).
Hence, the correct answer is option a) 3, 9, 15.
Find the sum of all two-digits odd positive integers.- a)2475
- b)2375
- c)2175
- d)1835
Correct answer is option 'B'. Can you explain this answer?
Find the sum of all two-digits odd positive integers.
a)
2475
b)
2375
c)
2175
d)
1835
|
|
Madhukar kamat answered |
To find the sum of all two-digit odd positive integers, we need to consider all the odd numbers between 10 and 99.
There are two main methods to solve this problem:
Method 1: Using the arithmetic series formula
1. The sum of an arithmetic series can be found using the formula: Sn = (n/2)(a + L), where Sn is the sum of the series, n is the number of terms, a is the first term, and L is the last term.
2. In this case, the first term is 11 (the smallest two-digit odd positive integer) and the last term is 99 (the largest two-digit odd positive integer).
3. The number of terms can be calculated by subtracting the first term from the last term and adding 1, then dividing by 2. In this case, (99 - 11 + 1)/2 = 45.
4. Plugging these values into the formula, we get Sn = (45/2)(11 + 99) = 22.5 * 110 = 2475.
Method 2: Using the sum of odd integers formula
1. The sum of all odd integers between 1 and n can be found using the formula: Sn = n^2, where Sn is the sum and n is the number of terms.
2. In this case, we need to find the sum of all odd integers between 1 and 99.
3. To find the number of terms, we need to count the odd integers in the range. We can observe that every second number is odd in this range, so the number of odd integers is equal to half of the number of integers between 1 and 99. Therefore, the number of terms is (99 - 1 + 1)/2 = 49.
4. Plugging these values into the formula, we get Sn = 49^2 = 2401.
5. However, we need to exclude the sum of all odd integers between 1 and 9, as these are not two-digit numbers. The sum of odd integers between 1 and 9 is 1 + 3 + 5 + 7 + 9 = 25.
6. Therefore, the final sum is 2401 - 25 = 2375.
Based on the methods used, the correct answer is option 'B' (2375).
There are two main methods to solve this problem:
Method 1: Using the arithmetic series formula
1. The sum of an arithmetic series can be found using the formula: Sn = (n/2)(a + L), where Sn is the sum of the series, n is the number of terms, a is the first term, and L is the last term.
2. In this case, the first term is 11 (the smallest two-digit odd positive integer) and the last term is 99 (the largest two-digit odd positive integer).
3. The number of terms can be calculated by subtracting the first term from the last term and adding 1, then dividing by 2. In this case, (99 - 11 + 1)/2 = 45.
4. Plugging these values into the formula, we get Sn = (45/2)(11 + 99) = 22.5 * 110 = 2475.
Method 2: Using the sum of odd integers formula
1. The sum of all odd integers between 1 and n can be found using the formula: Sn = n^2, where Sn is the sum and n is the number of terms.
2. In this case, we need to find the sum of all odd integers between 1 and 99.
3. To find the number of terms, we need to count the odd integers in the range. We can observe that every second number is odd in this range, so the number of odd integers is equal to half of the number of integers between 1 and 99. Therefore, the number of terms is (99 - 1 + 1)/2 = 49.
4. Plugging these values into the formula, we get Sn = 49^2 = 2401.
5. However, we need to exclude the sum of all odd integers between 1 and 9, as these are not two-digit numbers. The sum of odd integers between 1 and 9 is 1 + 3 + 5 + 7 + 9 = 25.
6. Therefore, the final sum is 2401 - 25 = 2375.
Based on the methods used, the correct answer is option 'B' (2375).
A manufacturer of laptop produced 6000 units in 3rd year and 7000 units in the 7th year. Assuming that production increases uniformly by a fixed number every year, find the production in the 5th year.- a)6500 units
- b)5000 units
- c)6000 units
- d)8000 units
Correct answer is option 'A'. Can you explain this answer?
A manufacturer of laptop produced 6000 units in 3rd year and 7000 units in the 7th year. Assuming that production increases uniformly by a fixed number every year, find the production in the 5th year.
a)
6500 units
b)
5000 units
c)
6000 units
d)
8000 units
|
|
Priyanka Kapoor answered |
Since, production of Laptops in 3rd year = 6000
⇒ a3 = 6000 ⇒ a + 2d = 6000 ...(i)
Also production of laptops in 7th year = 7000
a7 = 7000 ⇒ a + 6d = 7000 ...(ii)
Subtracting (i) from (ii), we get
4d = 1000 ⇒ d = 250
From (i), a + 2 (250) = 6000 ⇒ a = 5500
Hence, production in fifth year
a5 = a + 4d = (5500 + 4 (250)) = 6500 units
⇒ a3 = 6000 ⇒ a + 2d = 6000 ...(i)
Also production of laptops in 7th year = 7000
a7 = 7000 ⇒ a + 6d = 7000 ...(ii)
Subtracting (i) from (ii), we get
4d = 1000 ⇒ d = 250
From (i), a + 2 (250) = 6000 ⇒ a = 5500
Hence, production in fifth year
a5 = a + 4d = (5500 + 4 (250)) = 6500 units
The first, second and last term of an arithmetic progression are respectively 4, 7 and 31. How many terms are there in the given arithmetic progression?- a)14
- b)10
- c)9
- d)11
Correct answer is option 'B'. Can you explain this answer?
The first, second and last term of an arithmetic progression are respectively 4, 7 and 31. How many terms are there in the given arithmetic progression?
a)
14
b)
10
c)
9
d)
11
|
|
Ritu Saxena answered |
a = 4, d = 7 - 4 = 3, tn = 31
∴ tn = a + (n - 1)d
⇒ 31 = 4 + (n - 1) 3
⇒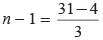
⇒ n - 1 = 9 ⇒ n = 10
∴ tn = a + (n - 1)d
⇒ 31 = 4 + (n - 1) 3
⇒
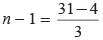
⇒ n - 1 = 9 ⇒ n = 10
Find the sum of first 25 terms of an arithmetic progression whose nth term is given by 7 - 3n.- a)800
- b)-800
- c)400
- d)-400
Correct answer is option 'B'. Can you explain this answer?
Find the sum of first 25 terms of an arithmetic progression whose nth term is given by 7 - 3n.
a)
800
b)
-800
c)
400
d)
-400
|
|
Ritu Saxena answered |
tn = 7 - 3n
t1 = 7 - 3 × 1 = 4 ⇒ a = 4
t2 = 7 - 3 × 2 = 1
d = 1 - 4 = -3
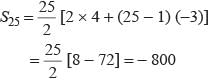
t1 = 7 - 3 × 1 = 4 ⇒ a = 4
t2 = 7 - 3 × 2 = 1
d = 1 - 4 = -3
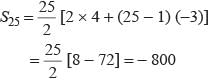
The ratio of the sum of m and n terms of an A.P. is m2 : n2, then find the ratio of mth and nth terms.- a)2m + 1 : 2n + 1
- b)2m – 1 : 2n – 1
- c)2m : n
- d)m : n
Correct answer is option 'B'. Can you explain this answer?
The ratio of the sum of m and n terms of an A.P. is m2 : n2, then find the ratio of mth and nth terms.
a)
2m + 1 : 2n + 1
b)
2m – 1 : 2n – 1
c)
2m : n
d)
m : n
|
|
Priyanka Kapoor answered |
We have, given that, 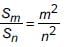
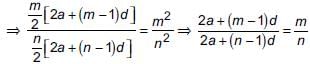
Replacing m with 2m – 1 and n with 2n – 1, we get
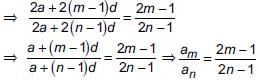
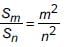
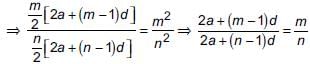
Replacing m with 2m – 1 and n with 2n – 1, we get
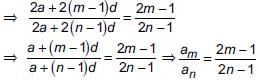
Four numbers are inserted between the numbers 4 and 39 such that an A.P. results. Find the biggest of these four numbers.- a)33
- b)31
- c)32
- d)30
Correct answer is option 'C'. Can you explain this answer?
Four numbers are inserted between the numbers 4 and 39 such that an A.P. results. Find the biggest of these four numbers.
a)
33
b)
31
c)
32
d)
30
|
|
Ramya menon answered |
To find the biggest of the four numbers inserted between 4 and 39 such that an arithmetic progression (A.P.) results, we can use the formula for the nth term of an arithmetic progression:
nth term (Tn) = a + (n - 1)d
where a is the first term, n is the position of the term, and d is the common difference.
Let's consider the A.P. with the first term as 4 and the last term as 39. Since we need to insert four numbers between them, the total number of terms in the A.P. will be 6 (including the first and last terms).
We need to find the biggest of the four numbers, which means we need to find the sixth term of the A.P.
1. Finding the common difference (d):
To find the common difference, we can use the formula:
common difference (d) = (last term - first term) / (number of terms - 1)
In this case, the last term is 39, the first term is 4, and the number of terms is 6.
d = (39 - 4) / (6 - 1) = 35 / 5 = 7
So, the common difference is 7.
2. Finding the sixth term (T6):
Now, we can use the formula for the nth term to find the sixth term (T6):
T6 = a + (n - 1)d
T6 = 4 + (6 - 1) * 7
= 4 + 5 * 7
= 4 + 35
= 39
Therefore, the biggest of the four numbers inserted between 4 and 39 such that an A.P. results is 39.
The correct answer is option 'C' (32) is incorrect.
nth term (Tn) = a + (n - 1)d
where a is the first term, n is the position of the term, and d is the common difference.
Let's consider the A.P. with the first term as 4 and the last term as 39. Since we need to insert four numbers between them, the total number of terms in the A.P. will be 6 (including the first and last terms).
We need to find the biggest of the four numbers, which means we need to find the sixth term of the A.P.
1. Finding the common difference (d):
To find the common difference, we can use the formula:
common difference (d) = (last term - first term) / (number of terms - 1)
In this case, the last term is 39, the first term is 4, and the number of terms is 6.
d = (39 - 4) / (6 - 1) = 35 / 5 = 7
So, the common difference is 7.
2. Finding the sixth term (T6):
Now, we can use the formula for the nth term to find the sixth term (T6):
T6 = a + (n - 1)d
T6 = 4 + (6 - 1) * 7
= 4 + 5 * 7
= 4 + 35
= 39
Therefore, the biggest of the four numbers inserted between 4 and 39 such that an A.P. results is 39.
The correct answer is option 'C' (32) is incorrect.
There are 25 trees at equal distances of 5 metres in a line with a well, the distance of the well from the nearest tree being 10 metres. A gardener waters all the trees separately starting from the well and he returns to the well after watering each tree to get water for the next. Find the total distance the gardner will cover in order to water all the trees.- a)3000 m
- b)3500 m
- c)3800 m
- d)4000 m
Correct answer is option 'B'. Can you explain this answer?
There are 25 trees at equal distances of 5 metres in a line with a well, the distance of the well from the nearest tree being 10 metres. A gardener waters all the trees separately starting from the well and he returns to the well after watering each tree to get water for the next. Find the total distance the gardner will cover in order to water all the trees.
a)
3000 m
b)
3500 m
c)
3800 m
d)
4000 m
|
|
Vivek Bansal answered |
Since, distance of nearest tree from the well = 10 m
Also, each tree is at equal distance of 5 m from the next tree.
∴ A.P. formed is 10, 15, 20, ...........
Here, a = 10, d = 5 and n = 25
S25 = (25/2)[2(10)+(25-1)5] = 1750
Hence, the total distance the gardener will cover in order to water all the trees = 2 × 1750 = 3500 m
Also, each tree is at equal distance of 5 m from the next tree.
∴ A.P. formed is 10, 15, 20, ...........
Here, a = 10, d = 5 and n = 25
S25 = (25/2)[2(10)+(25-1)5] = 1750
Hence, the total distance the gardener will cover in order to water all the trees = 2 × 1750 = 3500 m
The sum of the third and seventh terms of an A.P. is 6 and their product is 8. Find the sum of first sixteen terms of the A.P.- a)86
- b)90
- c)Both (A) and (B)
- d)None of these
Correct answer is option 'D'. Can you explain this answer?
The sum of the third and seventh terms of an A.P. is 6 and their product is 8. Find the sum of first sixteen terms of the A.P.
a)
86
b)
90
c)
Both (A) and (B)
d)
None of these
|
|
Priyanka Kapoor answered |
Let a be the first term and d be the common difference of the A.P.
We have, a3 + a7 = 6 and a3a7 = 8
⇒ (a + 2d) + (a + 6d) = 6 and (a + 2d) (a + 6d) = 8
⇒ 2a + 8d = 6 and (a + 2d) (a + 6d) = 8 ⇒ d = ±(1/2)
Case-I : When d =(1/2); a = 1 ⇒ S16 = 76
Case-II : When d = -(1/2); a = 5 ⇒ S16 = 20
We have, a3 + a7 = 6 and a3a7 = 8
⇒ (a + 2d) + (a + 6d) = 6 and (a + 2d) (a + 6d) = 8
⇒ 2a + 8d = 6 and (a + 2d) (a + 6d) = 8 ⇒ d = ±(1/2)
Case-I : When d =(1/2); a = 1 ⇒ S16 = 76
Case-II : When d = -(1/2); a = 5 ⇒ S16 = 20
The production of TV in a factory increases uniformly by a fixed number every year. It produced 8000 sets in 6th year and 11300 in 9th year. Find the production in the 6 years.- a)40500
- b)20000
- c)20500
- d)31500
Correct answer is option 'D'. Can you explain this answer?
The production of TV in a factory increases uniformly by a fixed number every year. It produced 8000 sets in 6th year and 11300 in 9th year. Find the production in the 6 years.
a)
40500
b)
20000
c)
20500
d)
31500
|
|
Subham Ghosh answered |
Given Data:
- TV production increases uniformly by a fixed number every year
- 8000 sets produced in the 6th year
- 11300 sets produced in the 9th year
Calculating the increase in production per year:
- Let the fixed increase be denoted by 'x'
- In the 6th year, the production is 8000 sets
- In the 9th year, the production is 11300 sets
- So, the increase in production over 3 years is (11300 - 8000) = 3300 sets
- This increase is due to the fixed increase 'x' each year
- So, 3x = 3300
- x = 1100
Calculating the production in the first 6 years:
- The production in the 6th year is 8000 sets
- So, the production in the 1st year would be (8000 - 5x) = (8000 - 5*1100) = 8000 - 5500 = 2500 sets
- Total production in the first 6 years = 6 * (2500 + 1100 + 2*1100 + 3*1100) = 6 * (2500 + 1100 + 2200 + 3300) = 6 * 9100 = 54600 sets
Therefore, the correct answer is option 'D' - 31500.
- TV production increases uniformly by a fixed number every year
- 8000 sets produced in the 6th year
- 11300 sets produced in the 9th year
Calculating the increase in production per year:
- Let the fixed increase be denoted by 'x'
- In the 6th year, the production is 8000 sets
- In the 9th year, the production is 11300 sets
- So, the increase in production over 3 years is (11300 - 8000) = 3300 sets
- This increase is due to the fixed increase 'x' each year
- So, 3x = 3300
- x = 1100
Calculating the production in the first 6 years:
- The production in the 6th year is 8000 sets
- So, the production in the 1st year would be (8000 - 5x) = (8000 - 5*1100) = 8000 - 5500 = 2500 sets
- Total production in the first 6 years = 6 * (2500 + 1100 + 2*1100 + 3*1100) = 6 * (2500 + 1100 + 2200 + 3300) = 6 * 9100 = 54600 sets
Therefore, the correct answer is option 'D' - 31500.
If the mth term of an arithmetic is 1/n and its nth term 1/m then what is its (mn)th term?- a)0
- b)m + n
- c)1
- d)-1
Correct answer is option 'A'. Can you explain this answer?
If the mth term of an arithmetic is 1/n and its nth term 1/m then what is its (mn)th term?
a)
0
b)
m + n
c)
1
d)
-1
|
|
Ritu Saxena answered |
Let a be the first term and d be the common difference
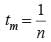
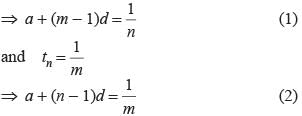
Subtracting eqn (2) from eqn (1)
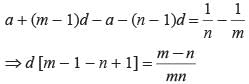
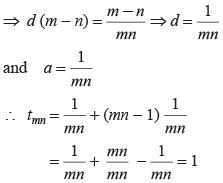
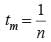
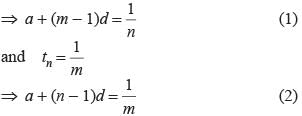
Subtracting eqn (2) from eqn (1)
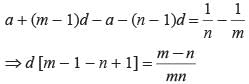
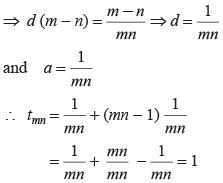
Find the sum of n terms of an arithmetic progression whose kth term is 5k + 1- a)
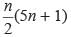
- b)
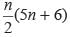
- c)
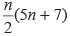
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
Find the sum of n terms of an arithmetic progression whose kth term is 5k + 1
a)
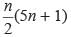
b)
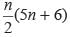
c)
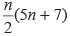
d)
None of these
|
|
Priyanka Kapoor answered |
tk = 5k + 1
t1 = 5 × 1 + 1 = 6
tn = 5n + 1
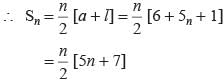
t1 = 5 × 1 + 1 = 6
tn = 5n + 1
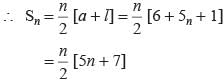
Find the sum of first 20 terms of an A.P. whose nth term is given by Tn = (7 – 3n).- a)382
- b)–490
- c)420
- d)–382
Correct answer is option 'B'. Can you explain this answer?
Find the sum of first 20 terms of an A.P. whose nth term is given by Tn = (7 – 3n).
a)
382
b)
–490
c)
420
d)
–382
|
|
Priyanka Kapoor answered |
We have, Tn = (7 – 3n)
First term, T1 = (7 – 3 × 1) = 4
Second term, T2 = 7 – 3 × 2 = 1
Third term, T3 = 7 – 3 × 3 = –2
∴ Series is 4, 1, – 2, .......... and common difference = –3
Sum of first 20 terms (S20)
= 20/2 [24 (20 - 1)(- 3)] = 10 [8 – 57] = –490
First term, T1 = (7 – 3 × 1) = 4
Second term, T2 = 7 – 3 × 2 = 1
Third term, T3 = 7 – 3 × 3 = –2
∴ Series is 4, 1, – 2, .......... and common difference = –3
Sum of first 20 terms (S20)
= 20/2 [24 (20 - 1)(- 3)] = 10 [8 – 57] = –490
If 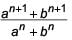 is the A.M. between a and b, then find the value of n.
is the A.M. between a and b, then find the value of n.- a)0
- b)1
- c)2
- d)3
Correct answer is option 'A'. Can you explain this answer?
If 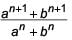 is the A.M. between a and b, then find the value of n.
is the A.M. between a and b, then find the value of n.
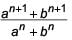 is the A.M. between a and b, then find the value of n.
is the A.M. between a and b, then find the value of n.a)
0
b)
1
c)
2
d)
3
|
|
Priyanka Kapoor answered |
A.M. between a and b = 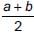
According to question,
⇒ aan + ban + abn + bbn = 2an + 1 + 2bn + 1
⇒ 2an + 1 + 2bn + 1 – an + 1 – ban – abn – bn + 1 = 0
⇒ an + 1 + bn + 1 – ban – abn = 0
⇒ an(a – b) – bn (a – b) = 0 ⇒ (a – b)(an – bn) = 0
But a – b ≠ 0 ⇒ an – bn = 0 ⇒ an = bn
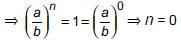
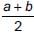
According to question,

⇒ aan + ban + abn + bbn = 2an + 1 + 2bn + 1
⇒ 2an + 1 + 2bn + 1 – an + 1 – ban – abn – bn + 1 = 0
⇒ an + 1 + bn + 1 – ban – abn = 0
⇒ an(a – b) – bn (a – b) = 0 ⇒ (a – b)(an – bn) = 0
But a – b ≠ 0 ⇒ an – bn = 0 ⇒ an = bn
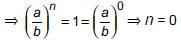
If pth, qth and rth terms of an arithmetic progression are a, b, c respectively, then what is the value of a(q - r) + b(r - p) + c(p - q)?- a)0
- b)1
- c)a + b + c
- d)p + d - r
Correct answer is option 'A'. Can you explain this answer?
If pth, qth and rth terms of an arithmetic progression are a, b, c respectively, then what is the value of a(q - r) + b(r - p) + c(p - q)?
a)
0
b)
1
c)
a + b + c
d)
p + d - r
|
|
Ritu Saxena answered |
Let x be the first term and d be the common difference.
pth term = a
x + (p - 1)d = a ...(1)
qth term = b ⇒ x + (q - 1)d = b ...(2)
rth term = c ⇒ x + (r - 1)d = c ...(3)
∴ a(q - r) + b(r - p) + c(p - q)
= x[q - r + r - p + p - q] + d[(p - 1) (q - r) + (q - 1) (r - p) + (r - 1) (q - q)]
⇒ a(q - r) + b(r - p) + c(p - q) = 0
pth term = a
x + (p - 1)d = a ...(1)
qth term = b ⇒ x + (q - 1)d = b ...(2)
rth term = c ⇒ x + (r - 1)d = c ...(3)
∴ a(q - r) + b(r - p) + c(p - q)
= x[q - r + r - p + p - q] + d[(p - 1) (q - r) + (q - 1) (r - p) + (r - 1) (q - q)]
⇒ a(q - r) + b(r - p) + c(p - q) = 0
If the mth term of an A.P. is 1/n and nth term is 1/m, then the sum of first mn terms is _______.- a)mn + 1
- b)(mn+1)/2
- c)(mn-1)/2
- d)(mn-1)/3
Correct answer is option 'B'. Can you explain this answer?
If the mth term of an A.P. is 1/n and nth term is 1/m, then the sum of first mn terms is _______.
a)
mn + 1
b)
(mn+1)/2
c)
(mn-1)/2
d)
(mn-1)/3
|
|
Priyanka Kapoor answered |
We have given, 
Then, a + (m-1)d = 1/n ...(i)
And, a + (n-1)d = 1/m ... (ii)
Subtracting (ii) from (i), we get,
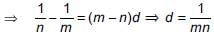
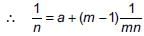 [From (i)]
[From (i)]
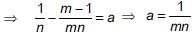
Now,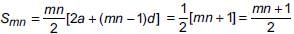

Then, a + (m-1)d = 1/n ...(i)
And, a + (n-1)d = 1/m ... (ii)
Subtracting (ii) from (i), we get,
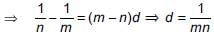
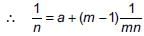 [From (i)]
[From (i)]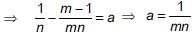
Now,
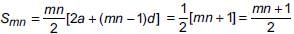
If in an arithmetic progression the sum of m terms is n and the sum of n terms is m then what is the sum of (m + n) terms?- a)m + n
- b)2m
- c)- (m + n)
- d)2n
Correct answer is option 'C'. Can you explain this answer?
If in an arithmetic progression the sum of m terms is n and the sum of n terms is m then what is the sum of (m + n) terms?
a)
m + n
b)
2m
c)
- (m + n)
d)
2n
|
|
Ritu Saxena answered |
Let a be the first term and d be the common difference.
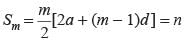
2am + m(m - 1)d = 2n (1)
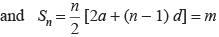
2an + n(n - 1)d = 2m (2)
Subtracting (2) from eqn (1), we get
2a(m - n) + [(m2 - n2) - (m - n)]d = 2(n - m)
⇒ (m - n)[2a + (m + n - 1) d] = 2(n - m)
2a + (m + n - 1)d = -2
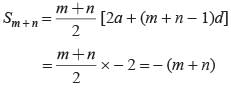
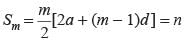
2am + m(m - 1)d = 2n (1)
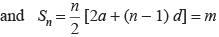
2an + n(n - 1)d = 2m (2)
Subtracting (2) from eqn (1), we get
2a(m - n) + [(m2 - n2) - (m - n)]d = 2(n - m)
⇒ (m - n)[2a + (m + n - 1) d] = 2(n - m)
2a + (m + n - 1)d = -2
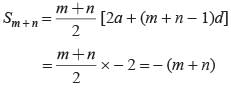
Fill in the blanks.
(i) If the ratio of sum of n terms of two A.P. is (7n + 1) : (4n + 27), then ratio of their mth terms is P .
(ii) Sum of n odd natural numbers is Q .
(iii) If sum of n terms of three A.P. are S1, S2, S3. The first term of each is 1 and common differance are 1, 2 and 3 respectively, then 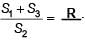
- a)
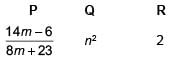
- b)
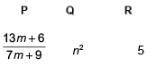
- c)
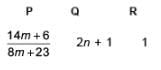
- d)
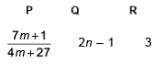
Correct answer is option 'A'. Can you explain this answer?
Fill in the blanks.
(i) If the ratio of sum of n terms of two A.P. is (7n + 1) : (4n + 27), then ratio of their mth terms is P .
(ii) Sum of n odd natural numbers is Q .
(iii) If sum of n terms of three A.P. are S1, S2, S3. The first term of each is 1 and common differance are 1, 2 and 3 respectively, then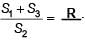
(i) If the ratio of sum of n terms of two A.P. is (7n + 1) : (4n + 27), then ratio of their mth terms is P .
(ii) Sum of n odd natural numbers is Q .
(iii) If sum of n terms of three A.P. are S1, S2, S3. The first term of each is 1 and common differance are 1, 2 and 3 respectively, then
a)
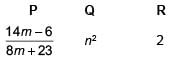
b)
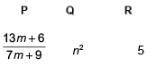
c)
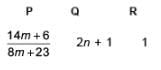
d)
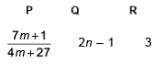
|
|
Priyanka Kapoor answered |
(i) Let Sn be the sum of n terms of 1st A.P. and S′n be sum of n terms of 2nd A.P.
According to question,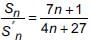
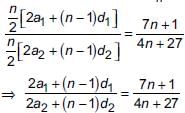
Put n = (2m – 1) in above equation, we get
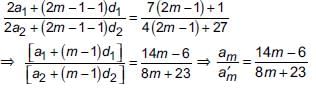
(ii) A.P. of odd n natural numbers is 1, 3, 5, ............

(iii) We have,
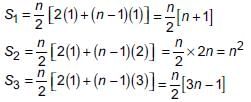
Now,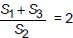
According to question,
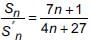
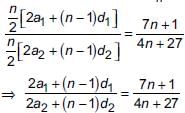
Put n = (2m – 1) in above equation, we get
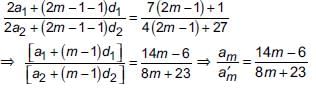
(ii) A.P. of odd n natural numbers is 1, 3, 5, ............

(iii) We have,
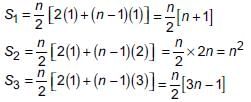
Now,
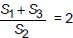
In an A.P., if the pth term is ‘q’ and the qth term is ‘p’, then its nth term is ________.- a)p + q – n
- b)p + q + n
- c)p – q + n
- d)p – q – n
Correct answer is option 'A'. Can you explain this answer?
In an A.P., if the pth term is ‘q’ and the qth term is ‘p’, then its nth term is ________.
a)
p + q – n
b)
p + q + n
c)
p – q + n
d)
p – q – n
|
|
Priyanka Kapoor answered |
We have given that ap = q and aq = p
⇒ q = a + (p – 1)d and ... (i)
p = a + (q – 1)d ... (ii)
Subtracting (ii) from (i), we get
q – p = d (p – q) ⇒ d = –1
Now, q = a + 1 – p [From (i)]
⇒ a = q + p – 1
∴ an = a + (n – 1) d = q + p – 1 + (n – 1) (– 1)
= q + p – 1 + 1 – n = q + p – n
⇒ q = a + (p – 1)d and ... (i)
p = a + (q – 1)d ... (ii)
Subtracting (ii) from (i), we get
q – p = d (p – q) ⇒ d = –1
Now, q = a + 1 – p [From (i)]
⇒ a = q + p – 1
∴ an = a + (n – 1) d = q + p – 1 + (n – 1) (– 1)
= q + p – 1 + 1 – n = q + p – n
In an A. P., the sum of first n terms is 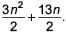 Find its 25th term.
Find its 25th term.- a)80
- b)120
- c)60
- d)78
Correct answer is option 'A'. Can you explain this answer?
In an A. P., the sum of first n terms is 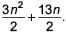 Find its 25th term.
Find its 25th term.
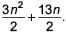 Find its 25th term.
Find its 25th term.a)
80
b)
120
c)
60
d)
78
|
|
Priyanka Kapoor answered |
We have given that 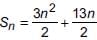
25th term = Sum of 25 terms – Sum of 24 terms
= S25 – S24
Now, S25 = 1100 and S24 = 1020
∴ 25th term = 1100 – 1020 = 80
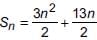
25th term = Sum of 25 terms – Sum of 24 terms
= S25 – S24
Now, S25 = 1100 and S24 = 1020
∴ 25th term = 1100 – 1020 = 80
If 9th term of an A.P. is zero, then its 29th term is ________ its 19th term.- a)Thrice of
- b)Twice of
- c)Half of
- d)Equal to
Correct answer is option 'B'. Can you explain this answer?
If 9th term of an A.P. is zero, then its 29th term is ________ its 19th term.
a)
Thrice of
b)
Twice of
c)
Half of
d)
Equal to
|
|
Priyanka Kapoor answered |
Let 1st term of A.P. be a and common difference be d.
Now, a9 = 0 ⇒ a + 8d = 0 ⇒ a = –8d ...(i)
Now, a29 = a + 28d = –8d + 28d
⇒ a29 = 20d ...(ii)
Also, a19 = a + 18d = –8d + 18d = 10d
⇒ 2 × a19 = 2 × 10d = 20d ...(iii)
From (ii) and (iii), we have
a29 = 2a19
Now, a9 = 0 ⇒ a + 8d = 0 ⇒ a = –8d ...(i)
Now, a29 = a + 28d = –8d + 28d
⇒ a29 = 20d ...(ii)
Also, a19 = a + 18d = –8d + 18d = 10d
⇒ 2 × a19 = 2 × 10d = 20d ...(iii)
From (ii) and (iii), we have
a29 = 2a19
If the sum of n terms of an arithmetic progression is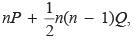 where P and Q are constants. What is the common difference?
where P and Q are constants. What is the common difference?- a)P
- b)P + Q
- c)2Q
- d)Q
Correct answer is option 'D'. Can you explain this answer?
If the sum of n terms of an arithmetic progression is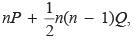 where P and Q are constants. What is the common difference?
where P and Q are constants. What is the common difference?
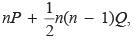 where P and Q are constants. What is the common difference?
where P and Q are constants. What is the common difference?a)
P
b)
P + Q
c)
2Q
d)
Q
|
|
Ritu Saxena answered |
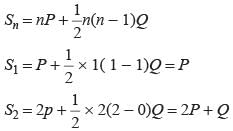
S2 - S1 = 2P + Q - P = P + Q
P, P + Q ….
Common difference = Q
How many terms of an arithmetic progression 3, 7, 11, 15, …. are taken so that the sum is 406?- a)14
- b)10
- c)12
- d)8
Correct answer is option 'A'. Can you explain this answer?
How many terms of an arithmetic progression 3, 7, 11, 15, …. are taken so that the sum is 406?
a)
14
b)
10
c)
12
d)
8
|
|
Priyanka Kapoor answered |
3, 7, 11, 15…..
a = 3, d = 4, Sn = 406
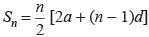
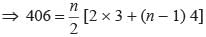
⇒ n[6 + 4n - 4] = 812
⇒ 4n2 + 2n = 812
⇒ 2n2 + n = 406
⇒ 2n2 + 29n - 28n - 406 = 0
⇒ n(2n + 29) × 14(2n + 29) = 0
⇒ (n - 14) (2n + 29) = 0
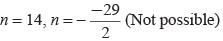
a = 3, d = 4, Sn = 406
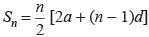
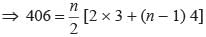
⇒ n[6 + 4n - 4] = 812
⇒ 4n2 + 2n = 812
⇒ 2n2 + n = 406
⇒ 2n2 + 29n - 28n - 406 = 0
⇒ n(2n + 29) × 14(2n + 29) = 0
⇒ (n - 14) (2n + 29) = 0
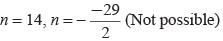
If S1, S2, S3, …. Sm are the sum of n terms of m arithmetic progression whose first terms are 1, 2, 3, …. m and common differences are 1, 3, 5, … (2m - 1) respectively. What is the value of S1 + S2 + …. Sm?- a)
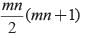
- b)
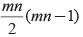
- c)
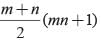
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
If S1, S2, S3, …. Sm are the sum of n terms of m arithmetic progression whose first terms are 1, 2, 3, …. m and common differences are 1, 3, 5, … (2m - 1) respectively. What is the value of S1 + S2 + …. Sm?
a)
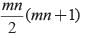
b)
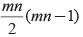
c)
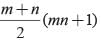
d)
None of these
|
|
Ritu Saxena answered |
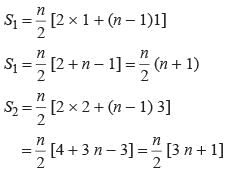
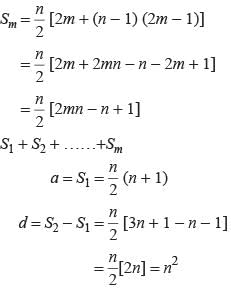
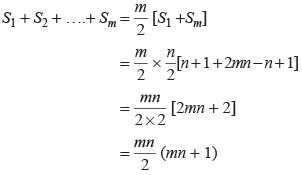
If four numbers in arithmetic progression are such that their sum is 50 and the greatest number is 4 times the least. Which number is the least one?- a)10
- b)15
- c)5
- d)20
Correct answer is option 'C'. Can you explain this answer?
If four numbers in arithmetic progression are such that their sum is 50 and the greatest number is 4 times the least. Which number is the least one?
a)
10
b)
15
c)
5
d)
20
|
|
Ritu Saxena answered |
Let the numbers are a -3d, a - d, a + d, a + 3d
a - 3d + a - d + a + d + a + 3d = 50
⇒ 4a = 50 ⇒ a = 50/4 = 25/2
a + 3d = 4(a - 3d )
⇒ a + 3d = 4a - 12d
⇒ 3a = 15d
⇒ a = 5d
⇒ 25/2 = 5d
⇒ d = 5/2
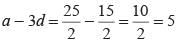
a - 3d + a - d + a + d + a + 3d = 50
⇒ 4a = 50 ⇒ a = 50/4 = 25/2
a + 3d = 4(a - 3d )
⇒ a + 3d = 4a - 12d
⇒ 3a = 15d
⇒ a = 5d
⇒ 25/2 = 5d
⇒ d = 5/2
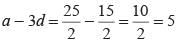
If x ≠ y and the sequences x, a1, a2, y and x, b1, b2, y each are in A.P., then 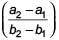 is ________.
is ________.- a)2/3
- b)3/2
- c)1
- d)3/4
Correct answer is option 'C'. Can you explain this answer?
If x ≠ y and the sequences x, a1, a2, y and x, b1, b2, y each are in A.P., then 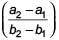 is ________.
is ________.
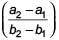 is ________.
is ________.a)
2/3
b)
3/2
c)
1
d)
3/4
|
|
Priyanka Kapoor answered |
For sequence, x, a1, a2, y
y = x + 3d ⇒ d = (y - x)/3
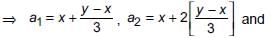
Similarly,
For sequence, x, b1, b2, y
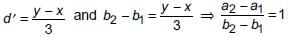
y = x + 3d ⇒ d = (y - x)/3
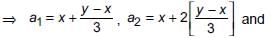
Similarly,

For sequence, x, b1, b2, y
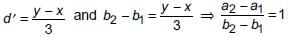
Which term of the A.P. 5, 2, –1, ....... is –22? - a)9
- b)11
- c)10
- d)7
Correct answer is option 'C'. Can you explain this answer?
Which term of the A.P. 5, 2, –1, ....... is –22?
a)
9
b)
11
c)
10
d)
7
|
|
Priyanka Kapoor answered |
Given A.P. is 5, 2, –1, ......
⇒ a = 5, d = 2 – 5 = –3
Tn = – 22 ⇒ a + (n – 1)d = –22
⇒ 5 + (n – 1) (–3) = –22 ⇒ n = 10
Hence, 10th term of the given A.P. is –22.
⇒ a = 5, d = 2 – 5 = –3
Tn = – 22 ⇒ a + (n – 1)d = –22
⇒ 5 + (n – 1) (–3) = –22 ⇒ n = 10
Hence, 10th term of the given A.P. is –22.
What is the nth term of the sequence log a, log ab, log ab2, log ab3, . . .- a)log b
- b)log anbn
- c)log (abn-1)
- d)log bn
Correct answer is option 'C'. Can you explain this answer?
What is the nth term of the sequence log a, log ab, log ab2, log ab3, . . .
a)
log b
b)
log anbn
c)
log (abn-1)
d)
log bn
|
|
Ritu Saxena answered |
loga, logab, logab2, logab3, ….
loga, loga + logb, loga + 2logb, loga + 3logb
t1 = loga, d = loga + logb - loga = logb
tn = t1 + (n - 1)d = loga + (n - 1)logb
= loga + logbn-1
= logabn-1
loga, loga + logb, loga + 2logb, loga + 3logb
t1 = loga, d = loga + logb - loga = logb
tn = t1 + (n - 1)d = loga + (n - 1)logb
= loga + logbn-1
= logabn-1
Which of the following statements is INCORRECT?(a) Sum of n terms of the list of numbers 
(b) The common difference of the A.P. given by an = 3n + 2 is 3.
(c) The sum of the A.P. (–5), (–8), (–11), ..., (–230) is – 8930.- a)Only (a)
- b)Only (b)
- c)Both (a) and (b)
- d)(a), (b) and (c)
Correct answer is option 'D'. Can you explain this answer?
Which of the following statements is INCORRECT?
(a) Sum of n terms of the list of numbers 
(b) The common difference of the A.P. given by an = 3n + 2 is 3.
(c) The sum of the A.P. (–5), (–8), (–11), ..., (–230) is – 8930.

(b) The common difference of the A.P. given by an = 3n + 2 is 3.
(c) The sum of the A.P. (–5), (–8), (–11), ..., (–230) is – 8930.
a)
Only (a)
b)
Only (b)
c)
Both (a) and (b)
d)
(a), (b) and (c)
|
|
Ritu Saxena answered |
(a) Given A.P. is 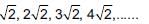
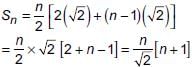
(b) Since, an = 3n + 2
Here, a1 = 3(1) + 2 = 5
a2 = 3(2) + 2 = 8
∴ Common difference = a2 – a1 = 3
(c) Given A.P. is (–5), (–8), (–11), ......, (–230)
⇒ an = a + (n – 1) (–3) ⇒ – 230 = –5 + (n – 1) (–3)
⇒(-225)/(-3) = (n-1) ⇒ n = 75 + 1 = 76
⇒ Sn = 76/2((-5)+(230))=-8930
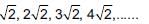
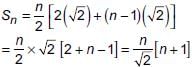
(b) Since, an = 3n + 2
Here, a1 = 3(1) + 2 = 5
a2 = 3(2) + 2 = 8
∴ Common difference = a2 – a1 = 3
(c) Given A.P. is (–5), (–8), (–11), ......, (–230)
⇒ an = a + (n – 1) (–3) ⇒ – 230 = –5 + (n – 1) (–3)
⇒(-225)/(-3) = (n-1) ⇒ n = 75 + 1 = 76
⇒ Sn = 76/2((-5)+(230))=-8930
How many terms are there in the Arithmetic Progression?
7, 11, 15, …..139?- a)32
- b)34
- c)31
- d)30
Correct answer is option 'B'. Can you explain this answer?
How many terms are there in the Arithmetic Progression?
7, 11, 15, …..139?
7, 11, 15, …..139?
a)
32
b)
34
c)
31
d)
30
|
|
Ritu Saxena answered |
Given AP is 7, 11, 15, ….139
Here a = 7, d = 11 - 7 = 4, l = 139
l = a + (n - 1) d
⇒ 139 = 7 + (n - 1) 4
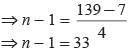
⇒ n = 34
Here a = 7, d = 11 - 7 = 4, l = 139
l = a + (n - 1) d
⇒ 139 = 7 + (n - 1) 4
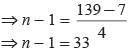
⇒ n = 34
Chapter doubts & questions for Arithmetic Progression - Olympiad Preparation for Class 10 2025 is part of Class 10 exam preparation. The chapters have been prepared according to the Class 10 exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Class 10 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Arithmetic Progression - Olympiad Preparation for Class 10 in English & Hindi are available as part of Class 10 exam.
Download more important topics, notes, lectures and mock test series for Class 10 Exam by signing up for free.

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup

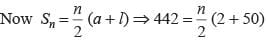
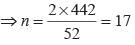

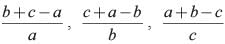 are in arithmetic progression then which of the following is correct?
are in arithmetic progression then which of the following is correct?