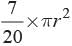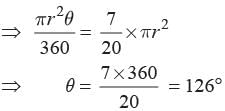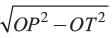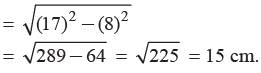All Exams >
Class 10 >
Olympiad Preparation for Class 10 >
All Questions
All questions of Circles for Class 10 Exam
The diameter of the front and rear wheels of a tractor are 80 cm and 200 cm respectively. What are the number of revolution that a rear wheel makes to cover the distance which the front wheel covers in 800 revolutions?- a)640
- b)320
- c)240
- d)300
Correct answer is option 'B'. Can you explain this answer?
The diameter of the front and rear wheels of a tractor are 80 cm and 200 cm respectively. What are the number of revolution that a rear wheel makes to cover the distance which the front wheel covers in 800 revolutions?
a)
640
b)
320
c)
240
d)
300
|
|
Aishwarya gupta answered |
To solve this problem, we can use the concept of the circumference of a circle and the relationship between the circumference and diameter.
Given:
Diameter of the front wheel = 80 cm
Diameter of the rear wheel = 200 cm
Step 1: Calculate the circumference of each wheel
Circumference of a circle = π * diameter
Circumference of the front wheel = π * 80 cm
Circumference of the rear wheel = π * 200 cm
Step 2: Find the ratio of the circumferences
Since the front and rear wheels are connected to the same axle, they will cover the same distance in one revolution. Therefore, the ratio of the circumferences is equal to the ratio of the number of revolutions.
Ratio of the circumferences = (Circumference of the rear wheel) / (Circumference of the front wheel)
Ratio of the circumferences = (π * 200 cm) / (π * 80 cm) = 200 cm / 80 cm = 5/2
Step 3: Find the number of revolutions the rear wheel makes to cover the distance covered by the front wheel in 800 revolutions
Since the ratio of the circumferences is equal to the ratio of the number of revolutions, we can set up the following proportion:
(Revolutions of the rear wheel) / 800 = 5/2
Cross-multiplying, we get:
2 * (Revolutions of the rear wheel) = 800 * 5
2 * (Revolutions of the rear wheel) = 4000
Revolutions of the rear wheel = 4000 / 2
Revolutions of the rear wheel = 2000
Therefore, the rear wheel makes 2000 revolutions to cover the distance covered by the front wheel in 800 revolutions.
Hence, the correct answer is option B) 320.
Given:
Diameter of the front wheel = 80 cm
Diameter of the rear wheel = 200 cm
Step 1: Calculate the circumference of each wheel
Circumference of a circle = π * diameter
Circumference of the front wheel = π * 80 cm
Circumference of the rear wheel = π * 200 cm
Step 2: Find the ratio of the circumferences
Since the front and rear wheels are connected to the same axle, they will cover the same distance in one revolution. Therefore, the ratio of the circumferences is equal to the ratio of the number of revolutions.
Ratio of the circumferences = (Circumference of the rear wheel) / (Circumference of the front wheel)
Ratio of the circumferences = (π * 200 cm) / (π * 80 cm) = 200 cm / 80 cm = 5/2
Step 3: Find the number of revolutions the rear wheel makes to cover the distance covered by the front wheel in 800 revolutions
Since the ratio of the circumferences is equal to the ratio of the number of revolutions, we can set up the following proportion:
(Revolutions of the rear wheel) / 800 = 5/2
Cross-multiplying, we get:
2 * (Revolutions of the rear wheel) = 800 * 5
2 * (Revolutions of the rear wheel) = 4000
Revolutions of the rear wheel = 4000 / 2
Revolutions of the rear wheel = 2000
Therefore, the rear wheel makes 2000 revolutions to cover the distance covered by the front wheel in 800 revolutions.
Hence, the correct answer is option B) 320.
A circle inscribed in DABC having AB = 10 cm, BC = 12 cm, CA = 28 cm touching sides at D, E, F (respectively). Then AD + BE + CF is ______.- a)25 cm
- b)20 cm
- c)22 cm
- d)18 cm
Correct answer is option 'A'. Can you explain this answer?
A circle inscribed in DABC having AB = 10 cm, BC = 12 cm, CA = 28 cm touching sides at D, E, F (respectively). Then AD + BE + CF is ______.
a)
25 cm
b)
20 cm
c)
22 cm
d)
18 cm
|
|
Vivek Bansal answered |
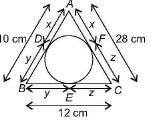
x + y = 10 cm ... (i)
y + z = 12 cm ... (ii)
x + z = 28cm ... (iii)
Adding (i), (ii) and (iii), we get
2(x + y + z) = 50
x + z = 28cm ... (iii)
Adding (i), (ii) and (iii), we get
2(x + y + z) = 50
⇒ x + y+ z = 25
In the given figure, AB and PQ intersect at M. If A and B are centres of circles then _______.- a)PM = MQ
- b)PQ ⊥ AB
- c) Both (A) and (B)
- d)PQ = AB
Correct answer is option 'C'. Can you explain this answer?
In the given figure, AB and PQ intersect at M. If A and B are centres of circles then _______.
a)
PM = MQ
b)
PQ ⊥ AB
c)
Both (A) and (B)
d)
PQ = AB
|
|
Saanvi choudhary answered |
In the given figure, AB and PQ intersect at M.
If A and B are centers of circles, then we can say that AM and BM are radii of the circle with center A and the circle with center B, respectively.
Therefore, AM = BM.
Since M is the point of intersection of AB and PQ, we can also say that PM and MQ are equal in length.
Therefore, the correct answer is:
a) PM = MQ
If A and B are centers of circles, then we can say that AM and BM are radii of the circle with center A and the circle with center B, respectively.
Therefore, AM = BM.
Since M is the point of intersection of AB and PQ, we can also say that PM and MQ are equal in length.
Therefore, the correct answer is:
a) PM = MQ
The radii of two concentric circles are 13 cm and 8 cm. AB is a diameter of the the bigger circle. BD is a tangent to the smaller circle touching it at D. Find the length AD.- a)19 cm
- b)20 cm
- c)16 cm
- d)√105
Correct answer is option 'A'. Can you explain this answer?
The radii of two concentric circles are 13 cm and 8 cm. AB is a diameter of the the bigger circle. BD is a tangent to the smaller circle touching it at D. Find the length AD.
a)
19 cm
b)
20 cm
c)
16 cm
d)
√105
|
|
Seema joshi answered |
To find the length AD, we can use the Pythagorean theorem.
Since AB is a diameter of the bigger circle, its length is equal to the diameter of the bigger circle, which is twice the radius. So, AB = 2 * 13 cm = 26 cm.
Since BD is tangent to the smaller circle, it is perpendicular to AD. Therefore, triangle ABD is a right triangle.
Using the Pythagorean theorem, we have:
(AD)^2 + (BD)^2 = (AB)^2
(AD)^2 + (8 cm)^2 = (26 cm)^2
(AD)^2 + 64 cm^2 = 676 cm^2
(AD)^2 = 676 cm^2 - 64 cm^2
(AD)^2 = 612 cm^2
AD = √(612 cm^2)
AD ≈ 24.7 cm
Therefore, the length AD is approximately 24.7 cm.
Since AB is a diameter of the bigger circle, its length is equal to the diameter of the bigger circle, which is twice the radius. So, AB = 2 * 13 cm = 26 cm.
Since BD is tangent to the smaller circle, it is perpendicular to AD. Therefore, triangle ABD is a right triangle.
Using the Pythagorean theorem, we have:
(AD)^2 + (BD)^2 = (AB)^2
(AD)^2 + (8 cm)^2 = (26 cm)^2
(AD)^2 + 64 cm^2 = 676 cm^2
(AD)^2 = 676 cm^2 - 64 cm^2
(AD)^2 = 612 cm^2
AD = √(612 cm^2)
AD ≈ 24.7 cm
Therefore, the length AD is approximately 24.7 cm.
Let s denote the semiperimeter of a triangle ABC in which BC = a, CA = b, AB = c. If a circle touches the sides BC, CA, AB at D, E, F, respectively, find BD.- a)s – b
- b)2s + h
- c)b + s
- d)3b – s
Correct answer is option 'A'. Can you explain this answer?
Let s denote the semiperimeter of a triangle ABC in which BC = a, CA = b, AB = c. If a circle touches the sides BC, CA, AB at D, E, F, respectively, find BD.
a)
s – b
b)
2s + h
c)
b + s
d)
3b – s
|
|
Niharika dasgupta answered |
By the property of a circle tangent to a line, we know that the line segment from the center of the circle to the point of tangency is perpendicular to the line. Therefore, let O be the center of the circle and let M, N, and P be the midpoints of BC, CA, and AB respectively.
Since O is the incenter of triangle ABC, O is equidistant from the sides of the triangle. Therefore, OM = ON = OP.
We can draw radii from O to the points of tangency D, E, and F. Let r be the length of these radii. Then, OD = OE = OF = r.
Since OM = ON = OP, we have that MD = NE = PF = s - a, where s is the semiperimeter of triangle ABC.
By the Pythagorean Theorem, we have that BD^2 = BM^2 + MD^2. Since BM = a/2 and MD = s - a, we have that BD^2 = (a/2)^2 + (s - a)^2.
Expanding and simplifying, we have that BD^2 = a^2/4 + s^2 - 2as + a^2.
Rearranging terms, we have that BD^2 = s^2 - 2as + a^2/4 + a^2.
Factoring, we have that BD^2 = (s - a/2)^2 + a^2/4.
Taking the square root of both sides, we have that BD = sqrt((s - a/2)^2 + a^2/4).
Therefore, the length of BD is sqrt((s - a/2)^2 + a^2/4).
Answer: a) sqrt((s - a/2)^2 + a^2/4)
Since O is the incenter of triangle ABC, O is equidistant from the sides of the triangle. Therefore, OM = ON = OP.
We can draw radii from O to the points of tangency D, E, and F. Let r be the length of these radii. Then, OD = OE = OF = r.
Since OM = ON = OP, we have that MD = NE = PF = s - a, where s is the semiperimeter of triangle ABC.
By the Pythagorean Theorem, we have that BD^2 = BM^2 + MD^2. Since BM = a/2 and MD = s - a, we have that BD^2 = (a/2)^2 + (s - a)^2.
Expanding and simplifying, we have that BD^2 = a^2/4 + s^2 - 2as + a^2.
Rearranging terms, we have that BD^2 = s^2 - 2as + a^2/4 + a^2.
Factoring, we have that BD^2 = (s - a/2)^2 + a^2/4.
Taking the square root of both sides, we have that BD = sqrt((s - a/2)^2 + a^2/4).
Therefore, the length of BD is sqrt((s - a/2)^2 + a^2/4).
Answer: a) sqrt((s - a/2)^2 + a^2/4)
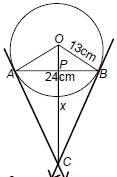
AB is a chord of length 24 cm of a circle of radius 13 cm. The tangents at A and B intersect at a point C. Find the length AC.- a)31.2 cm
- b)12 cm
- c)28.8 cm
- d)25 cm
Correct answer is option 'A'. Can you explain this answer?
AB is a chord of length 24 cm of a circle of radius 13 cm. The tangents at A and B intersect at a point C. Find the length AC.
a)
31.2 cm
b)
12 cm
c)
28.8 cm
d)
25 cm
|
|
Ritu Saxena answered |
Given, Chord AB = 24 cm, Radius OB = OA = 13 cm.
Draw OP ⊥ AB
In D OPB, OP ⊥ AB ⇒ AP = PB
[Perpendicular from centre on chord bisect the chord] =(1/2)AB= 12
Also, OB2 = OP2 + PB2
⇒ (13)2 = OP2 + PB2 ⇒ 169 = OP2 + (12)2
⇒ OP2 = 169 - 144 = 25 ⇒ OP = 5 cm
In Δ BPC, BC2 = x2 + BP2 [By pythagoras theorem]
BC2 = x2 + 144 ...(i)
In ΔOBC, OC2 = OB2 + BC2
⇒ (x + 5)2 = (13)2 + BC2 ⇒ x = 288/10=28.8cm
Put the value of x in (i), we get
BC2 = x2 + 144 = ((144)2/25) + 144⇒ BC = 31.2
⇒ AC = BC = 31.2 cm
Draw OP ⊥ AB
In D OPB, OP ⊥ AB ⇒ AP = PB
[Perpendicular from centre on chord bisect the chord] =(1/2)AB= 12
Also, OB2 = OP2 + PB2
⇒ (13)2 = OP2 + PB2 ⇒ 169 = OP2 + (12)2
⇒ OP2 = 169 - 144 = 25 ⇒ OP = 5 cm
In Δ BPC, BC2 = x2 + BP2 [By pythagoras theorem]
BC2 = x2 + 144 ...(i)
In ΔOBC, OC2 = OB2 + BC2
⇒ (x + 5)2 = (13)2 + BC2 ⇒ x = 288/10=28.8cm

Put the value of x in (i), we get
BC2 = x2 + 144 = ((144)2/25) + 144⇒ BC = 31.2
⇒ AC = BC = 31.2 cm
In a circle of radius 10.5 cm, the minor arc is one-fifth of the major arc. What is the area of major arc?- a)288.75 cm2
- b)281.75 cm2
- c)271.25 cm2
- d)262.75 cm2
Correct answer is option 'A'. Can you explain this answer?
In a circle of radius 10.5 cm, the minor arc is one-fifth of the major arc. What is the area of major arc?
a)
288.75 cm2
b)
281.75 cm2
c)
271.25 cm2
d)
262.75 cm2

|
Neha Sharma answered |
To find the area of the major arc, we first need to determine the measure of the central angle corresponding to the major arc.
Let's assume the measure of the major arc is x degrees. Since the minor arc is one-fifth of the major arc, the measure of the minor arc would be x/5 degrees.
We know that the measure of a central angle is directly proportional to the length of the arc it intercepts. So, we can write the proportion:
x/360 = (x/5)/(2πr)
where r is the radius of the circle.
Simplifying the equation, we get:
x/360 = (x/5)/(2π(10.5))
x/360 = x/(5 * 2π * 10.5)
x/360 = x/(105π)
Cross multiplying, we have:
105π * x = 360 * x
105π = 360
x = (360 * π) / 105
x ≈ 10.2857 degrees
So, the measure of the major arc is approximately 10.2857 degrees.
Now, to find the area of the major arc, we can use the formula:
Area = (θ/360) * π * r²
where θ is the measure of the central angle in degrees and r is the radius of the circle.
Plugging in the values, we get:
Area = (10.2857/360) * π * (10.5)²
Area ≈ (0.0286) * (3.14) * (10.5)²
Area ≈ 0.897 * 110.25
Area ≈ 98.72525 cm²
Therefore, the area of the major arc is approximately 98.72525 cm², which can be rounded to 98.73 cm². None of the given options match this value.
However, if we round the area to the nearest hundredth, it becomes 98.73 cm², which is closest to option 'A' (288.75 cm²).
Let's assume the measure of the major arc is x degrees. Since the minor arc is one-fifth of the major arc, the measure of the minor arc would be x/5 degrees.
We know that the measure of a central angle is directly proportional to the length of the arc it intercepts. So, we can write the proportion:
x/360 = (x/5)/(2πr)
where r is the radius of the circle.
Simplifying the equation, we get:
x/360 = (x/5)/(2π(10.5))
x/360 = x/(5 * 2π * 10.5)
x/360 = x/(105π)
Cross multiplying, we have:
105π * x = 360 * x
105π = 360
x = (360 * π) / 105
x ≈ 10.2857 degrees
So, the measure of the major arc is approximately 10.2857 degrees.
Now, to find the area of the major arc, we can use the formula:
Area = (θ/360) * π * r²
where θ is the measure of the central angle in degrees and r is the radius of the circle.
Plugging in the values, we get:
Area = (10.2857/360) * π * (10.5)²
Area ≈ (0.0286) * (3.14) * (10.5)²
Area ≈ 0.897 * 110.25
Area ≈ 98.72525 cm²
Therefore, the area of the major arc is approximately 98.72525 cm², which can be rounded to 98.73 cm². None of the given options match this value.
However, if we round the area to the nearest hundredth, it becomes 98.73 cm², which is closest to option 'A' (288.75 cm²).
The perimeter of a sector of a circle of radius 5.2 cm is 16.4 cm, then what is area of sector?- a)14.6 cm2
- b)15.6 cm2
- c)19.6 cm2
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
The perimeter of a sector of a circle of radius 5.2 cm is 16.4 cm, then what is area of sector?
a)
14.6 cm2
b)
15.6 cm2
c)
19.6 cm2
d)
None of these
|
|
Priyanka Kapoor answered |
Let O be the centre of a circle of radius 5.2 cm. Let OABO be the sector with perimeter 16.4 cm.
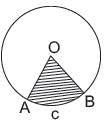
OA + O B + arc AB = 27.2
5.2 + 5 .2 + arc AB = 16.4
⇒ arc AB = 16.4 - 16.4 = 6 cm
Area of sector OACBO
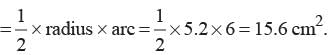

OA + O B + arc AB = 27.2
5.2 + 5 .2 + arc AB = 16.4
⇒ arc AB = 16.4 - 16.4 = 6 cm
Area of sector OACBO
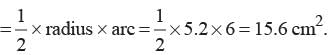
A field is in the form of a circle. The cost of ploughing the field at Rs. 1.50 per m2 is Rs. 5775. Find the cost of fencing the field at Rs. 8.50 per meter.- a)Rs. 1870
- b)Rs. 1670
- c)Rs. 1980
- d)Rs. 1780
Correct answer is option 'A'. Can you explain this answer?
A field is in the form of a circle. The cost of ploughing the field at Rs. 1.50 per m2 is Rs. 5775. Find the cost of fencing the field at Rs. 8.50 per meter.
a)
Rs. 1870
b)
Rs. 1670
c)
Rs. 1980
d)
Rs. 1780
|
|
Sarita iyer answered |
Cost of Ploughing the Field
- Given cost of ploughing the field = Rs. 5775
- Cost per m2 = Rs. 1.50
- Area of the circular field = Cost / Cost per m2 = 5775 / 1.50 = 3850 m2
Cost of Fencing the Field
- Cost per meter of fencing = Rs. 8.50
- Circumference of the circle = 2 * π * r, where r is the radius
- Radius (r) of the circular field = √(Area / π) = √(3850 / π) ≈ 35 m
- Circumference = 2 * π * 35 ≈ 219.91 m
Total Cost of Fencing
- Total cost of fencing = Cost per meter * Circumference = 8.50 * 219.91 ≈ Rs. 1870
Therefore, the cost of fencing the field at Rs. 8.50 per meter is approximately Rs. 1870.
- Given cost of ploughing the field = Rs. 5775
- Cost per m2 = Rs. 1.50
- Area of the circular field = Cost / Cost per m2 = 5775 / 1.50 = 3850 m2
Cost of Fencing the Field
- Cost per meter of fencing = Rs. 8.50
- Circumference of the circle = 2 * π * r, where r is the radius
- Radius (r) of the circular field = √(Area / π) = √(3850 / π) ≈ 35 m
- Circumference = 2 * π * 35 ≈ 219.91 m
Total Cost of Fencing
- Total cost of fencing = Cost per meter * Circumference = 8.50 * 219.91 ≈ Rs. 1870
Therefore, the cost of fencing the field at Rs. 8.50 per meter is approximately Rs. 1870.
The minute hand of a clock is 12 cm long. Find the area of the face of the clock described by the minute hand in 35 minutes.- a)252 cm2
- b)264 cm2
- c)184 cm2
- d)1284 cm2
Correct answer is option 'B'. Can you explain this answer?
The minute hand of a clock is 12 cm long. Find the area of the face of the clock described by the minute hand in 35 minutes.
a)
252 cm2
b)
264 cm2
c)
184 cm2
d)
1284 cm2
|
|
Smita das answered |
To find the area of the face of the clock described by the minute hand in 35 minutes, we need to find the length of the arc covered by the minute hand and then use it to calculate the area.
Length of Arc Covered by the Minute Hand:
The minute hand of the clock is 12 cm long. In 60 minutes, it covers a complete circle, which is equivalent to the circumference of the clock face. The formula for the circumference of a circle is given by:
C = 2πr
where C is the circumference and r is the radius.
In this case, the radius is equal to the length of the minute hand, which is 12 cm. So, the circumference of the clock face is:
C = 2π(12) = 24π cm
In 60 minutes, the minute hand covers the entire circumference. Therefore, in 35 minutes, it covers:
35/60 * 24π = 7/12 * 24π = 14π cm
Area of the Face of the Clock:
To find the area of the face of the clock described by the minute hand in 35 minutes, we need to calculate the area of the sector formed by the minute hand.
The formula for the area of a sector of a circle is given by:
A = (θ/360) * πr^2
where A is the area, θ is the central angle in degrees, and r is the radius.
In this case, the central angle is 35/60 * 360 = 210 degrees (since the minute hand covers 35 minutes out of 60 minutes, and each minute corresponds to 6 degrees on the clock face).
Substituting the values into the formula, we get:
A = (210/360) * π(12)^2
= (7/12) * π(144)
= 7π * 12
= 84π cm^2
Approximating π to 3.14, we have:
Area = 84 * 3.14
≈ 264 cm^2
Therefore, the area of the face of the clock described by the minute hand in 35 minutes is approximately 264 cm^2.
Hence, option B is the correct answer.
Length of Arc Covered by the Minute Hand:
The minute hand of the clock is 12 cm long. In 60 minutes, it covers a complete circle, which is equivalent to the circumference of the clock face. The formula for the circumference of a circle is given by:
C = 2πr
where C is the circumference and r is the radius.
In this case, the radius is equal to the length of the minute hand, which is 12 cm. So, the circumference of the clock face is:
C = 2π(12) = 24π cm
In 60 minutes, the minute hand covers the entire circumference. Therefore, in 35 minutes, it covers:
35/60 * 24π = 7/12 * 24π = 14π cm
Area of the Face of the Clock:
To find the area of the face of the clock described by the minute hand in 35 minutes, we need to calculate the area of the sector formed by the minute hand.
The formula for the area of a sector of a circle is given by:
A = (θ/360) * πr^2
where A is the area, θ is the central angle in degrees, and r is the radius.
In this case, the central angle is 35/60 * 360 = 210 degrees (since the minute hand covers 35 minutes out of 60 minutes, and each minute corresponds to 6 degrees on the clock face).
Substituting the values into the formula, we get:
A = (210/360) * π(12)^2
= (7/12) * π(144)
= 7π * 12
= 84π cm^2
Approximating π to 3.14, we have:
Area = 84 * 3.14
≈ 264 cm^2
Therefore, the area of the face of the clock described by the minute hand in 35 minutes is approximately 264 cm^2.
Hence, option B is the correct answer.
A copper wire when bent in the form of a square encloses an area of 484 cm2. The same wire is now bent in the form of a circle. Find the area enclosed by the circle.- a)616 cm2
- b)456 cm2
- c)216 cm2
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
A copper wire when bent in the form of a square encloses an area of 484 cm2. The same wire is now bent in the form of a circle. Find the area enclosed by the circle.
a)
616 cm2
b)
456 cm2
c)
216 cm2
d)
None of these

|
Anoushka Nambiar answered |
To solve this problem, we need to use the formulas for the area of a square and the area of a circle.
1. Area of a square:
The area of a square can be found by multiplying the length of one side by itself. Therefore, if the copper wire is bent in the form of a square and encloses an area of 484 cm^2, we can find the length of one side using the formula:
Area of square = side^2
484 = side^2
Taking the square root of both sides, we get:
side = √484
side = 22 cm
2. Perimeter of a square:
The perimeter of a square can be found by multiplying the length of one side by 4. In this case, the perimeter of the square formed by the copper wire is:
Perimeter of square = 4 * side
Perimeter of square = 4 * 22
Perimeter of square = 88 cm
3. Circumference of a circle:
The circumference of a circle can be found using the formula:
Circumference = π * diameter
Since the copper wire is bent in the form of a square, the length of the wire is equal to the perimeter of the square. Therefore, the circumference of the circle formed by the copper wire is:
Circumference of circle = 88 cm
4. Radius of the circle:
To find the radius of the circle, we can use the formula:
Radius = Circumference / (2 * π)
Radius = 88 / (2 * 3.14)
Radius ≈ 14 cm
5. Area of a circle:
Finally, we can find the area of the circle using the formula:
Area of circle = π * radius^2
Area of circle = 3.14 * 14^2
Area of circle ≈ 3.14 * 196
Area of circle ≈ 615.44 cm^2
Therefore, the area enclosed by the circle formed by the copper wire is approximately 616 cm^2, which corresponds to option A.
1. Area of a square:
The area of a square can be found by multiplying the length of one side by itself. Therefore, if the copper wire is bent in the form of a square and encloses an area of 484 cm^2, we can find the length of one side using the formula:
Area of square = side^2
484 = side^2
Taking the square root of both sides, we get:
side = √484
side = 22 cm
2. Perimeter of a square:
The perimeter of a square can be found by multiplying the length of one side by 4. In this case, the perimeter of the square formed by the copper wire is:
Perimeter of square = 4 * side
Perimeter of square = 4 * 22
Perimeter of square = 88 cm
3. Circumference of a circle:
The circumference of a circle can be found using the formula:
Circumference = π * diameter
Since the copper wire is bent in the form of a square, the length of the wire is equal to the perimeter of the square. Therefore, the circumference of the circle formed by the copper wire is:
Circumference of circle = 88 cm
4. Radius of the circle:
To find the radius of the circle, we can use the formula:
Radius = Circumference / (2 * π)
Radius = 88 / (2 * 3.14)
Radius ≈ 14 cm
5. Area of a circle:
Finally, we can find the area of the circle using the formula:
Area of circle = π * radius^2
Area of circle = 3.14 * 14^2
Area of circle ≈ 3.14 * 196
Area of circle ≈ 615.44 cm^2
Therefore, the area enclosed by the circle formed by the copper wire is approximately 616 cm^2, which corresponds to option A.
The side of a square is 10 cm. What is the area of circumscribed circle?- a)78.5 cm2
- b)157 cm2
- c)135 cm2
- d)314 cm2
Correct answer is option 'B'. Can you explain this answer?
The side of a square is 10 cm. What is the area of circumscribed circle?
a)
78.5 cm2
b)
157 cm2
c)
135 cm2
d)
314 cm2

|
Ashish Choudhary answered |
Given:
Side of the square = 10 cm
To find:
The area of the circumscribed circle.
Solution:
To find the area of the circumscribed circle, we need to find the radius of the circle first.
Finding the radius:
The diagonal of a square divides it into two congruent right-angled triangles.
Let's consider one of these triangles.
In a right-angled triangle, the hypotenuse (diagonal of the square) is equal to the diameter of the circle and the length of one side of the square is equal to the radius of the circle.
Using the Pythagorean theorem, we can find the length of the diagonal of the square:
(diagonal)^2 = (side)^2 + (side)^2
(diagonal)^2 = 10^2 + 10^2
(diagonal)^2 = 100 + 100
(diagonal)^2 = 200
diagonal = √200 = 10√2 cm
Since the diagonal of the square is equal to the diameter of the circle, the diameter of the circle is 10√2 cm.
So, the radius of the circle = (10√2)/2 = 5√2 cm.
Finding the area of the circle:
The area of a circle is given by the formula: A = πr^2, where r is the radius of the circle.
Substituting the value of the radius, we get:
A = π(5√2)^2
A = π(25*2)
A = 50π cm^2
Now, let's approximate the value of π to 3.14.
A ≈ 50 * 3.14
A ≈ 157 cm^2
Therefore, the area of the circumscribed circle is approximately 157 cm^2.
Answer:
The correct answer is option b) 157 cm^2.
Side of the square = 10 cm
To find:
The area of the circumscribed circle.
Solution:
To find the area of the circumscribed circle, we need to find the radius of the circle first.
Finding the radius:
The diagonal of a square divides it into two congruent right-angled triangles.
Let's consider one of these triangles.
In a right-angled triangle, the hypotenuse (diagonal of the square) is equal to the diameter of the circle and the length of one side of the square is equal to the radius of the circle.
Using the Pythagorean theorem, we can find the length of the diagonal of the square:
(diagonal)^2 = (side)^2 + (side)^2
(diagonal)^2 = 10^2 + 10^2
(diagonal)^2 = 100 + 100
(diagonal)^2 = 200
diagonal = √200 = 10√2 cm
Since the diagonal of the square is equal to the diameter of the circle, the diameter of the circle is 10√2 cm.
So, the radius of the circle = (10√2)/2 = 5√2 cm.
Finding the area of the circle:
The area of a circle is given by the formula: A = πr^2, where r is the radius of the circle.
Substituting the value of the radius, we get:
A = π(5√2)^2
A = π(25*2)
A = 50π cm^2
Now, let's approximate the value of π to 3.14.
A ≈ 50 * 3.14
A ≈ 157 cm^2
Therefore, the area of the circumscribed circle is approximately 157 cm^2.
Answer:
The correct answer is option b) 157 cm^2.
Two circles of radii 10 cm and 8 cm intersect each other and the length of common chord is 12 cm. The distance between their centres is.- a)√7 cm
- b)3√7 cm
- c)4√7 cm
- d)(8 + 2√7) cm
Correct answer is option 'D'. Can you explain this answer?
Two circles of radii 10 cm and 8 cm intersect each other and the length of common chord is 12 cm. The distance between their centres is.
a)
√7 cm
b)
3√7 cm
c)
4√7 cm
d)
(8 + 2√7) cm
|
|
Vivek Bansal answered |
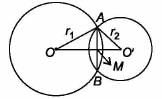
M is the mid-point of AB,
∴ AM = 6 cm
AO (r1) = 10 cm,
AO' (r2) = 8 cm
AB is perpendicular to OO' , then
In ΔAOM, 100 = 36 + OM2 [using pythagoras theorem]
⇒ OM = 8 cm; In ΔAMO', 64 = 36 + MO'2
⇒ √28 = MO' = 2√7 = MO'
∴ OO' = (2√7 + 8) cm
How the tangent at any point of a circle and radius through the point is related?- a)perpendicular to each other
- b)parallel to each other
- c)having same length
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
How the tangent at any point of a circle and radius through the point is related?
a)
perpendicular to each other
b)
parallel to each other
c)
having same length
d)
none of these
|
|
Rohit Sharma answered |
The tangent at any point of a circle and the radius through this point are perpendicular to each other as shown below:
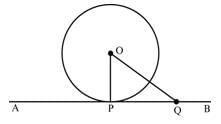
In the figure above,
∠OPA +∠OPQ = 180∘ ........(1) [Linear pair angle]
Also, ∠OPA = ∠OPQ ......(2)
∴ ∠OPA +∠OPQ = 180∘
2 ×∠OPQ = 180∘
∠OPQ = 90∘
Hence, OP is perpendicular to PQ ⇒ OP is perpendicular to AB.

In the figure above,
∠OPA +∠OPQ = 180∘ ........(1) [Linear pair angle]
Also, ∠OPA = ∠OPQ ......(2)
∴ ∠OPA +∠OPQ = 180∘
2 ×∠OPQ = 180∘
∠OPQ = 90∘
Hence, OP is perpendicular to PQ ⇒ OP is perpendicular to AB.
What is the area of circle in which the difference between the radius and circumference of the circle be 37 cm?- a)144 cm2
- b)154 cm2
- c)124 cm2
- d)224 cm2
Correct answer is option 'B'. Can you explain this answer?
What is the area of circle in which the difference between the radius and circumference of the circle be 37 cm?
a)
144 cm2
b)
154 cm2
c)
124 cm2
d)
224 cm2
|
|
Priyanka Kapoor answered |
Let r be the radius of the circle
2πr - r = 37
⇒ r (2π - 1) = 37
⇒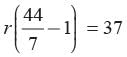
⇒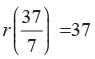
2πr - r = 37
⇒ r (2π - 1) = 37
⇒
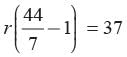
⇒
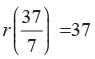
⇒ r = 7 cm
Area = πr2 = 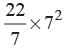 = 22 × 7 = 154 cm2.
= 22 × 7 = 154 cm2.
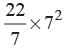 = 22 × 7 = 154 cm2.
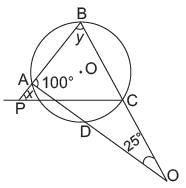
= 22 × 7 = 154 cm2.What is the value of y and x respectively in the given figure?
- a)x = 55°, y = 45°
- b)x = 45°, y = 55°
- c)x = 65°, y = 55°
- d)x = 55°, y = 65°
Correct answer is option 'B'. Can you explain this answer?
What is the value of y and x respectively in the given figure?


a)
x = 55°, y = 45°
b)
x = 45°, y = 55°
c)
x = 65°, y = 55°
d)
x = 55°, y = 65°
|
|
Priyanka Kapoor answered |
In ΔABO,
∠y + 25° + 100° = 180°
⇒ y = 55°
∠C + ∠A = 180° [∵ ABCD is cycle]
⇒ ∠ = 80°
In ΔPBC,
∠x + 55° + 80° = 180°
⇒ ∠x = 45°
∠y + 25° + 100° = 180°
⇒ y = 55°
∠C + ∠A = 180° [∵ ABCD is cycle]
⇒ ∠ = 80°
In ΔPBC,
∠x + 55° + 80° = 180°
⇒ ∠x = 45°
A bicycle wheel makes 5000 revolutions in moving 11 km. What is the radius of the wheel?- a)45 cm
- b)25 cm
- c)35 cm
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
A bicycle wheel makes 5000 revolutions in moving 11 km. What is the radius of the wheel?
a)
45 cm
b)
25 cm
c)
35 cm
d)
None of these
|
|
Priyanka Kapoor answered |
Distance moved by wheel
= 2 × π × r × 5000 = 11000 m
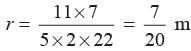
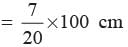
= 2 × π × r × 5000 = 11000 m
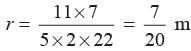
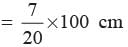
= 35 cm
In the given figure, O is the centre of the circle, then ∠OZ is______.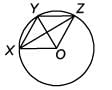
- a)2 ∠XZY
- b)2 ∠Y
- c)2 ∠Z
- d)2 (∠XZY + ∠YXZ)
Correct answer is option 'D'. Can you explain this answer?
In the given figure, O is the centre of the circle, then ∠OZ is______.

a)
2 ∠XZY
b)
2 ∠Y
c)
2 ∠Z
d)
2 (∠XZY + ∠YXZ)
|
|
Ritu Saxena answered |
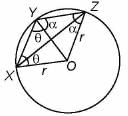
OX= OY = OZ = r (radius of circle)
Taking ∠X = θ and ∠Z = α
Then in ΔYXO, OX = OY ⇒ ∠X = ∠OYX = θ
Now, in ΔOZY OZ= OY⇒ ∠Z= ∠OYZ = α
Now, XOZY is a quadrilateral,
⇒ ∠X+∠Y+ ∠Z+∠O = 360°
⇒ θ + θ + α + α +∠O = 360°
⇒ ∠O = 360° - 2(α + θ)
⇒ ∠O = 360° - 2 (∠OZX + ∠XZY + ∠OXZ + ∠ZXY)
⇒ ∠O = 360° - 2 (∠OZX + ∠OXZ) - 2(∠XZY + ∠ZXY)
⇒ ∠O = 360° - 2(180° - ∠O) - 2(∠XZY + ∠ZXY)
⇒ ∠O = 360° - 360° + 2∠O - 2(∠XZY + ∠ZXY)
Taking ∠X = θ and ∠Z = α
Then in ΔYXO, OX = OY ⇒ ∠X = ∠OYX = θ
Now, in ΔOZY OZ= OY⇒ ∠Z= ∠OYZ = α
Now, XOZY is a quadrilateral,
⇒ ∠X+∠Y+ ∠Z+∠O = 360°
⇒ θ + θ + α + α +∠O = 360°
⇒ ∠O = 360° - 2(α + θ)
⇒ ∠O = 360° - 2 (∠OZX + ∠XZY + ∠OXZ + ∠ZXY)
⇒ ∠O = 360° - 2 (∠OZX + ∠OXZ) - 2(∠XZY + ∠ZXY)
⇒ ∠O = 360° - 2(180° - ∠O) - 2(∠XZY + ∠ZXY)
⇒ ∠O = 360° - 360° + 2∠O - 2(∠XZY + ∠ZXY)
Match the columns.
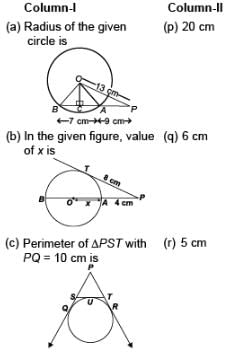
- a)(a) → (p), (b) → (r), (c) → (q)
- b)(a) → (r), (b) → (q), (c) → (p)
- c)(a) → (q), (b) → (r), (c) → (p)
- d)(a) → (r), (b) → (p), (c) → (q)
Correct answer is option 'B'. Can you explain this answer?
Match the columns.


a)
(a) → (p), (b) → (r), (c) → (q)
b)
(a) → (r), (b) → (q), (c) → (p)
c)
(a) → (q), (b) → (r), (c) → (p)
d)
(a) → (r), (b) → (p), (c) → (q)
|
|
Ritu Saxena answered |
(a) Draw OC perpendicular on AB,
In Δ OBC & Δ OAC
∠OCB = ∠OCA (each 90°)
OB = OA (radii of same circle)
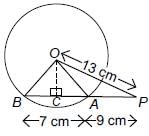
OC is common side in both triangles
∴ ΔOBC ≅ ΔOAC (RHS congruence)
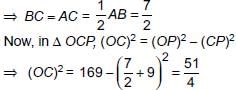
Now, in ΔOCA (OA)2 = (OC)2 + (CA)2
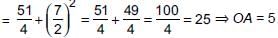
Hence, radius of circle = 5 cm
(b) : In ΔOPT,
(OP)2 = (OT)2 + (PT)2
⇒ (x + 4)2 = x2 + (8)2
⇒ x2 + 16 + 8x = x2 + 64
⇒ 8x = 48 ⇒ x = 6 cm
(c) : PQ = 10 cm
We know, length of tangents drawn from an external point to a circle are equal.
⇒ PQ = PR ...(i)
Also, SQ = SU ...(ii)
and TU = TR ...(iii)
Now, perimeter of DPST
= PS + ST + PT = PS + SU + UT + PT
= PS + SQ + TR + PT (Using (ii) & (iii))
= PQ + PR = PQ + PQ (Using (i))
= 2 PQ = 2 × 10 = 20 cm.
In Δ OBC & Δ OAC
∠OCB = ∠OCA (each 90°)
OB = OA (radii of same circle)

OC is common side in both triangles
∴ ΔOBC ≅ ΔOAC (RHS congruence)
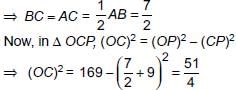
Now, in ΔOCA (OA)2 = (OC)2 + (CA)2
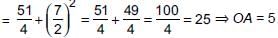
Hence, radius of circle = 5 cm
(b) : In ΔOPT,
(OP)2 = (OT)2 + (PT)2
⇒ (x + 4)2 = x2 + (8)2
⇒ x2 + 16 + 8x = x2 + 64
⇒ 8x = 48 ⇒ x = 6 cm
(c) : PQ = 10 cm
We know, length of tangents drawn from an external point to a circle are equal.
⇒ PQ = PR ...(i)
Also, SQ = SU ...(ii)
and TU = TR ...(iii)
Now, perimeter of DPST
= PS + ST + PT = PS + SU + UT + PT
= PS + SQ + TR + PT (Using (ii) & (iii))
= PQ + PR = PQ + PQ (Using (i))
= 2 PQ = 2 × 10 = 20 cm.
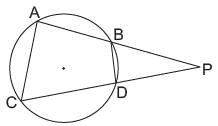
Two chords AB and CD of a circle intersect at an external point P as shown in figure. If AB = 8 cm, BP = 10 cm, PD = 12 cm. What is length of CP?
- a)15 cm
- b)12 cm
- c)18 cm
- d)10 cm
Correct answer is option 'A'. Can you explain this answer?
Two chords AB and CD of a circle intersect at an external point P as shown in figure. If AB = 8 cm, BP = 10 cm, PD = 12 cm. What is length of CP?


a)
15 cm
b)
12 cm
c)
18 cm
d)
10 cm
|
|
Priyanka Kapoor answered |
For any external point P,
AP × BP = PD × PC
⇒ (AB + BP) × BP = 12 × PC
⇒ (8 +10) × 10 = 12 × PC
⇒ PC =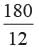 = 15 cm.
= 15 cm.
AP × BP = PD × PC
⇒ (AB + BP) × BP = 12 × PC
⇒ (8 +10) × 10 = 12 × PC
⇒ PC =
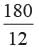 = 15 cm.
= 15 cm.In the following figure, PT is of length 8 cm. OP is 10 cm. Then the radius of the circle is___.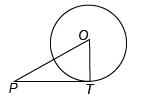
- a)2 cm
- b)18 cm
- c)(5/4) cm
- d)6 cm
Correct answer is option 'D'. Can you explain this answer?
In the following figure, PT is of length 8 cm. OP is 10 cm. Then the radius of the circle is___.

a)
2 cm
b)
18 cm
c)
(5/4) cm
d)
6 cm
|
|
Priyanka Kapoor answered |
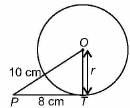
Since OT is perpendicular to FT, Using pythagoras theorem,
100 = 64 + r2
100 = 64 + r2
∴ r = 6 cm
In the given figure, PT touches the circle at R whose centre is O. Diameter SQ when produced meets PT at P. Given ∠SPR = x° and ∠QRP = y°. Then,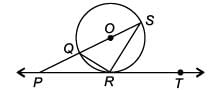
- a)x° + 2y° = 90°
- b)2x° + y° = 90°
- c)x° + y° = 120°
- d)3x°+2y° = 120°
Correct answer is option 'A'. Can you explain this answer?
In the given figure, PT touches the circle at R whose centre is O. Diameter SQ when produced meets PT at P. Given ∠SPR = x° and ∠QRP = y°. Then,

a)
x° + 2y° = 90°
b)
2x° + y° = 90°
c)
x° + y° = 120°
d)
3x°+2y° = 120°
|
|
Vivek Bansal answered |
Consider chord QR
∴∠QRP = ∠QSR
⇒ ∠QSR = y° [∴ QRP = y°]
⇒ ∠PSR = y°
Since angle in a semicircle is a right angle.
∴∠QRS = 90°
Now, ∠PRS = ∠QRP + ∠QRS
⇒ ∠PRS = y° + 90°
In ΔPRS, we have
∠SPR + ∠PRS + ∠PSR = 180°
⇒ x° + y°+ 90° + y° = 180°
⇒ x° + 2y° = 90°
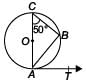
If O is the centre of a circle, AOC is its diameter and B is a point on the circle such that ∠ACB = 50°. If AT is the tangent to the circle at the point A, then ∠BAT =
- a)40°
- b)50°
- c)60°
- d)65°
Correct answer is option 'B'. Can you explain this answer?
If O is the centre of a circle, AOC is its diameter and B is a point on the circle such that ∠ACB = 50°. If AT is the tangent to the circle at the point A, then ∠BAT =


a)
40°
b)
50°
c)
60°
d)
65°
|
|
Ritu Saxena answered |
∠ABC = 90° [Angle in a semicircle ]
In ∆ ABC, we have
∠ACB + ∠CAB + ∠ABC = 180°
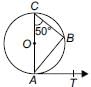
⇒ 50° + ∠CAB + 90° = 180°
⇒ ∠CAB = 40°
Now, ∠CAT = 90° ⇒ ∠CAB + ∠BAT = 90°
⇒ 40° + ∠BAT = 90°⇒ ∠BAT = 50°
In ∆ ABC, we have
∠ACB + ∠CAB + ∠ABC = 180°

⇒ 50° + ∠CAB + 90° = 180°
⇒ ∠CAB = 40°
Now, ∠CAT = 90° ⇒ ∠CAB + ∠BAT = 90°
⇒ 40° + ∠BAT = 90°⇒ ∠BAT = 50°
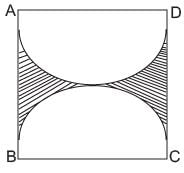
What is the area of shaded region if ABCD is a square of side 14 cm and APD and BPC are semi circles?
- a)52 cm2
- b)32 cm2
- c)42 cm2
- d)62 cm2
Correct answer is option 'C'. Can you explain this answer?
What is the area of shaded region if ABCD is a square of side 14 cm and APD and BPC are semi circles?


a)
52 cm2
b)
32 cm2
c)
42 cm2
d)
62 cm2
|
|
Priyanka Kapoor answered |
Area of the shaded region = Area of square ABCD - Area of two semicircles
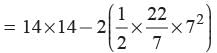
= 196 - 154 = 42 cm2
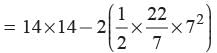
= 196 - 154 = 42 cm2
In the given figure, O is the centre of the circle and TP is the tangent to the circle from an external point T. If ∠PBT = 30°, then BA : AT is
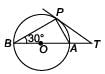
- a)3 : 1
- b)4 : 1
- c)2 : 1
- d)3 : 2
Correct answer is option 'C'. Can you explain this answer?
In the given figure, O is the centre of the circle and TP is the tangent to the circle from an external point T. If ∠PBT = 30°, then BA : AT is


a)
3 : 1
b)
4 : 1
c)
2 : 1
d)
3 : 2
|
|
Ritu Saxena answered |
∠BPA = 90° (Angle in semicircle)
In ∆ BPA, ∠ABP + ∠BPA + ∠PAB = 180°
⇒ 30° + 90° + ∠PAB = 180°
⇒ ∠PAB = 60°
Also, ∠POA = 2∠PBA
⇒ ∠POA = 2 × 30° = 60°
⇒ OP = AP ...(i)
(side opposite to equal angles)
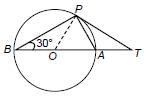
In ∆OPT, ∠OPT = 90°
∠POT = 60° and ∠PTO = 30° [angle sum property of a D]
Also ∠APT + ∠ATP = ∠PAO [exterior angle property]
∴ ∠APT + 30°= 60° ⇒ ∠APT = 30°
∴ AP = AT ...(ii) (side opposite to equal angles)
From (i) and (ii), AT = OP = radius of the circle; and AB = 2r
⇒ AB = 2AT ⇒ AB/AT = 2 ⇒ AB : AT = 2 :1
In ∆ BPA, ∠ABP + ∠BPA + ∠PAB = 180°
⇒ 30° + 90° + ∠PAB = 180°
⇒ ∠PAB = 60°
Also, ∠POA = 2∠PBA
⇒ ∠POA = 2 × 30° = 60°
⇒ OP = AP ...(i)
(side opposite to equal angles)

In ∆OPT, ∠OPT = 90°
∠POT = 60° and ∠PTO = 30° [angle sum property of a D]
Also ∠APT + ∠ATP = ∠PAO [exterior angle property]
∴ ∠APT + 30°= 60° ⇒ ∠APT = 30°
∴ AP = AT ...(ii) (side opposite to equal angles)
From (i) and (ii), AT = OP = radius of the circle; and AB = 2r
⇒ AB = 2AT ⇒ AB/AT = 2 ⇒ AB : AT = 2 :1
Two concentric circles of radii a and b, where a > b, are given. The length of a chord of the larger circle which touches the other circle is- a)
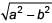
- b)
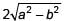
- c)
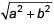
- d)
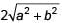
Correct answer is option 'B'. Can you explain this answer?
Two concentric circles of radii a and b, where a > b, are given. The length of a chord of the larger circle which touches the other circle is
a)
b)
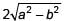
c)
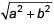
d)
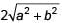
|
|
Ritu Saxena answered |
In figure, AB is a chord of circle C1 which is a tangent to C2.
Since, tangent is perpendicular to radius through point of contact
∴ ∠OCA = 90° ⇒ OA = a, OC = b
In ∆OCA, (OA)2 = (OC)2 + (AC)2
⇒ a2 = b2 + (AC)2 ⇒ AC =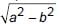
∴ Length of chord AB = 2AC = 2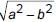

Since, tangent is perpendicular to radius through point of contact
∴ ∠OCA = 90° ⇒ OA = a, OC = b
In ∆OCA, (OA)2 = (OC)2 + (AC)2
⇒ a2 = b2 + (AC)2 ⇒ AC =
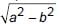
∴ Length of chord AB = 2AC = 2
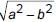

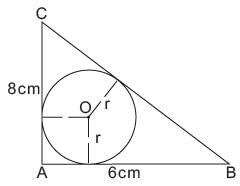
In the given figure, DABC is right angled at A with AB = 6 cm and AC = 8 cm. A circle with centre O has been inscribed inside the triangle. Find the value of the radius of the inscribed circle.
- a)2 cm
- b)3 cm
- c)4 cm
- d)5 cm
Correct answer is option 'A'. Can you explain this answer?
In the given figure, DABC is right angled at A with AB = 6 cm and AC = 8 cm. A circle with centre O has been inscribed inside the triangle. Find the value of the radius of the inscribed circle.


a)
2 cm
b)
3 cm
c)
4 cm
d)
5 cm
|
|
Priyanka Kapoor answered |
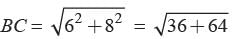
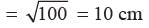
(area DOAC) + (area DOAB) + (area DOBC)
= area (DABC)
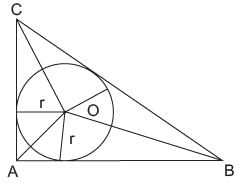
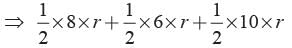
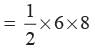
⇒ 8r + 6r + 10r = 48
⇒ 24r = 48 ⇒ r = 2
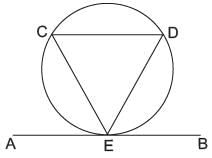
AB is a tangent to the circle at E. If EC = ED and ∠CDE = 62°. Find angle ∠AED.
- a)118°
- b)100°
- c)108°
- d)98°
Correct answer is option 'A'. Can you explain this answer?
AB is a tangent to the circle at E. If EC = ED and ∠CDE = 62°. Find angle ∠AED.


a)
118°
b)
100°
c)
108°
d)
98°
|
|
Priyanka Kapoor answered |
∵ EC = ED
∴ ∠ECD = ∠EDC = 62°
∴ ∠DEC = 180° - (2 × 62°) =56°
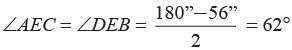 ∴ ∠AED = ∠CED + ∠AEC
∴ ∠AED = ∠CED + ∠AEC
= 56° + 62° = 118°
∴ ∠ECD = ∠EDC = 62°
∴ ∠DEC = 180° - (2 × 62°) =56°
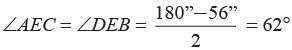 ∴ ∠AED = ∠CED + ∠AEC
∴ ∠AED = ∠CED + ∠AEC= 56° + 62° = 118°
A bucket is raised from a well by means of a rope which is wound round a wheel of diameter 77 cm. Given that the bucket ascends in 1 minute 28 seconds with a uniform speed of 1.1 m/s. What is the number of complete revolutions the wheel makes in raising the bucket?- a)60
- b)50
- c)30
- d)40
Correct answer is option 'D'. Can you explain this answer?
A bucket is raised from a well by means of a rope which is wound round a wheel of diameter 77 cm. Given that the bucket ascends in 1 minute 28 seconds with a uniform speed of 1.1 m/s. What is the number of complete revolutions the wheel makes in raising the bucket?
a)
60
b)
50
c)
30
d)
40
|
|
Priyanka Kapoor answered |
Distance moved by rope
= (1.1) × (60 + 28)
∴ No. of revolutions =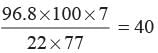
= (1.1) × (60 + 28)
∴ No. of revolutions =
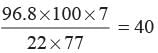
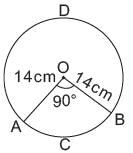
A chord of a circle of radius 14 cm makes a right angle at the centre. Find the area of minor segment of the circle.
- a)98 cm2
- b)56 cm2
- c)16 cm2
- d)64 cm2
Correct answer is option 'B'. Can you explain this answer?
A chord of a circle of radius 14 cm makes a right angle at the centre. Find the area of minor segment of the circle.


a)
98 cm2
b)
56 cm2
c)
16 cm2
d)
64 cm2
|
|
Priyanka Kapoor answered |
Area of the sector OACBO,
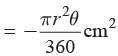
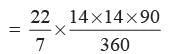
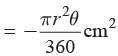
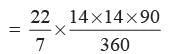
= 154 cm2.
Area of ΔOAB =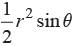
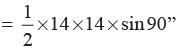
∴ Area of minor segment of circle
= 154 - 98 = 56 cm2.
Area of ΔOAB =
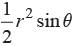
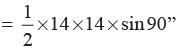
∴ Area of minor segment of circle
= 154 - 98 = 56 cm2.
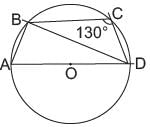
In the given figure AD is diameter of the circle. If ∠BCD = 130°. What is the value of ∠DAB?
- a)50°
- b)65°
- c)40°
- d)70°
Correct answer is option 'A'. Can you explain this answer?
In the given figure AD is diameter of the circle. If ∠BCD = 130°. What is the value of ∠DAB?


a)
50°
b)
65°
c)
40°
d)
70°
|
|
Priyanka Kapoor answered |
∵ A, B, C and D are on the circumference of the circle.
∴ ABCD is a cyclic quadrilateral, i.e.,
∠A + ∠C = 180°
⇒ ∠A = 180° - ∠C = 180° - 130° = 50°
∴ ∠DAB= 50°.
∴ ABCD is a cyclic quadrilateral, i.e.,
∠A + ∠C = 180°
⇒ ∠A = 180° - ∠C = 180° - 130° = 50°
∴ ∠DAB= 50°.
In the given figure, a circle touches the side BC of ΔABC at P and touches AB and AC produced at Q and R respectively. If AQ = 5 cm, find the perimeter of ΔABC.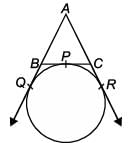
- a)11 cm
- b)10 cm
- c)6 cm
- d)7 cm
Correct answer is option 'B'. Can you explain this answer?
In the given figure, a circle touches the side BC of ΔABC at P and touches AB and AC produced at Q and R respectively. If AQ = 5 cm, find the perimeter of ΔABC.

a)
11 cm
b)
10 cm
c)
6 cm
d)
7 cm
|
|
Vivek Bansal answered |
Perimeter of ΔABC = AB + BC + AC
= AB + (BP + PC) + AC
= (AB + BQ) + (CR + AC)
= (AB + BQ) + (CR + AC)
[∵ BP = BQ,PC = CR]
= AQ + AR
(∵AQ = AR, tangents of circle from same point A)
(∵AQ = AR, tangents of circle from same point A)
= 2 AQ = 2 x 5 = 10 cm
In the given figure, O is the centre and SAT is a tangent to the circle at A. If ∠BAT = 30°, find ∠AOB and ∠AQB.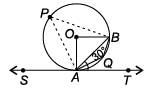
- a)60°, 150°
- b)30°, 150°
- c)60°, 60°
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
In the given figure, O is the centre and SAT is a tangent to the circle at A. If ∠BAT = 30°, find ∠AOB and ∠AQB.

a)
60°, 150°
b)
30°, 150°
c)
60°, 60°
d)
None of these
|
|
Ritu Saxena answered |
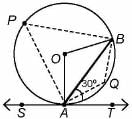
∠BAT = 30° (given) Since angle made by chord with a tangent is equal to angle made by it in alternate segment.
∴ ∠APB = 30°
Now, ∠APB + ∠AQB = 180°
Now, ∠APB + ∠AQB = 180°
[Opposite angles of cyclic quadrilateral APBQ]
⇒ 30° + ∠AQB = 180° ⇒ ∠AQB = 150°
Also, ∠AOB = 60° [Angle subtended by an arc at centre is double the angle subtended by it on remaining part of circle]
∴ ∠AOB = 60°, ∠AQB = 150°
In the given figure, a circle touches all the four sides of a quadrilateral ABCD whose three sides are AB = 6 cm, BC = 7 cm, CD = 4 cm, then AD equals _________.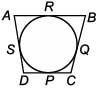
- a) 10 cm
- b) 13 cm
- c) 11 cm
- d) 3 cm
Correct answer is option 'D'. Can you explain this answer?
In the given figure, a circle touches all the four sides of a quadrilateral ABCD whose three sides are AB = 6 cm, BC = 7 cm, CD = 4 cm, then AD equals _________.

a)
10 cm
b)
13 cm
c)
11 cm
d)
3 cm
|
|
Priyanka Kapoor answered |
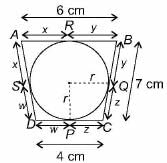
x + y = 6 cm ... (i)
y + z = 7 cm ... (ii)
z + w = 4 cm ... (iii)
Using (ii) and (iii),
y - w = 3 cm
Now using (i) x + (3 + w) = 6 cm
⇒ x + w = 3 cm
⇒ AD = 3 cm
In the given figure, O is the centre of the circle. If PA and PB are tangents, then the value of ∠AQB is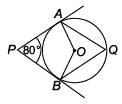
- a)100°
- b)80°
- c)60°
- d)50°
Correct answer is option 'D'. Can you explain this answer?
In the given figure, O is the centre of the circle. If PA and PB are tangents, then the value of ∠AQB is

a)
100°
b)
80°
c)
60°
d)
50°
|
|
Ritu Saxena answered |
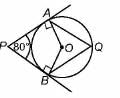
Since PA and PB are tangents.
Also, tangent is ⊥ r to radius through point of contact,
Also, tangent is ⊥ r to radius through point of contact,
∴ ∠PAO = 90° and ∠PBO = 90°
In quadrilateral APBO
∠APB + ∠PAO + ∠PBO + ∠AOB = 360°
80° + 90° + 90° + ∠AOB = 360°
⇒ ∠AOB = 100° ⇒ ∠AQB = 1/2∠AOB = 50°
80° + 90° + 90° + ∠AOB = 360°
⇒ ∠AOB = 100° ⇒ ∠AQB = 1/2∠AOB = 50°
A square park has each side of 100 m. At each comer of the park, there is a flower bed in the form of a quadrant inside the park of radius 14 m. What is the area of remaining part?- a)9384 m2
- b)9684 m2
- c)9224 m2
- d)9386 m2
Correct answer is option 'A'. Can you explain this answer?
A square park has each side of 100 m. At each comer of the park, there is a flower bed in the form of a quadrant inside the park of radius 14 m. What is the area of remaining part?
a)
9384 m2
b)
9684 m2
c)
9224 m2
d)
9386 m2
|
|
Priyanka Kapoor answered |
Let A be the area of each quadrant of the circle.
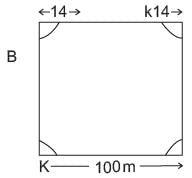
Radius of circel = 14 cm
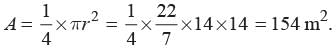
Area of 4 quadrants = 4 ×154 = 616 m2 Area of square park = (100)2 = 10000 m2
Area of remaining part = 10000 - 616
= 9384 m2

Radius of circel = 14 cm
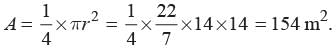
Area of 4 quadrants = 4 ×154 = 616 m2 Area of square park = (100)2 = 10000 m2
Area of remaining part = 10000 - 616
= 9384 m2
A race track is in the form of a ring whose inner and outer circumference are 437 m and 503 m respectively. Find the area of the track.- a)4935 m2
- b)4065 m2
- c)4135 m2
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
A race track is in the form of a ring whose inner and outer circumference are 437 m and 503 m respectively. Find the area of the track.
a)
4935 m2
b)
4065 m2
c)
4135 m2
d)
None of these

|
Nk Classes answered |
Let R be the radius of outer circle and r be the radius of inner circle
2πR = 503
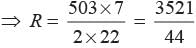
and 2πr = 437
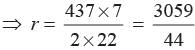
Width of the track = R - r =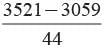
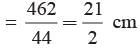
2πR = 503
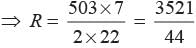
and 2πr = 437
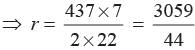
Width of the track = R - r =
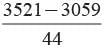
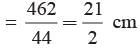
Area of the track = π(R2 - r2)
= π(R + r) (R - r)
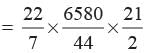
= 4935 m2
= π(R + r) (R - r)
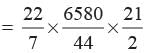
= 4935 m2
A Pendulum swings through an angle of 30° and describes an arc 8.8 cm in length, then what is the length of the Pendulum?- a)16.8 cm
- b)12.8 cm
- c)14.2 cm
- d)15.6 cm
Correct answer is option 'A'. Can you explain this answer?
A Pendulum swings through an angle of 30° and describes an arc 8.8 cm in length, then what is the length of the Pendulum?
a)
16.8 cm
b)
12.8 cm
c)
14.2 cm
d)
15.6 cm
|
|
Priyanka Kapoor answered |
Length of pendulum
= radius of the sector = x cm.
Arc length = 8.8 cm
⇒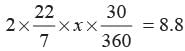
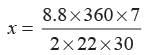
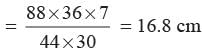
= radius of the sector = x cm.
Arc length = 8.8 cm
⇒
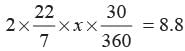
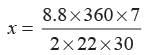
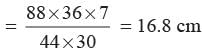
What is the area of quadrant of a circle whose circumference is 22 cm?- a)9.625 cm2
- b)10.625 cm2
- c)6.75 cm2
- d)8.75 cm2
Correct answer is option 'A'. Can you explain this answer?
What is the area of quadrant of a circle whose circumference is 22 cm?
a)
9.625 cm2
b)
10.625 cm2
c)
6.75 cm2
d)
8.75 cm2
|
|
Priyanka Kapoor answered |
Let r be the radius
2πr = 22
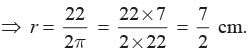
Area of quadrant =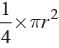
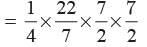
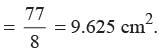
2πr = 22
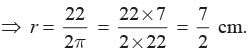
Area of quadrant =
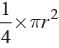
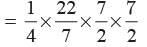
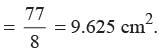
What is the length of tangent drawn from a point whose distance from the centre of a circle is 25 cm, if radius of the circle is 7 cm?- a)24 cm
- b)25 cm
- c)26 cm
- d)30 cm
Correct answer is option 'A'. Can you explain this answer?
What is the length of tangent drawn from a point whose distance from the centre of a circle is 25 cm, if radius of the circle is 7 cm?
a)
24 cm
b)
25 cm
c)
26 cm
d)
30 cm
|
|
Priyanka Kapoor answered |

PT2 + OT2 = OP2
⇒ PT2 = (25)2 -(7)2
⇒ PT =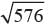 = 24 cm.
= 24 cm.
⇒ PT2 = (25)2 -(7)2
⇒ PT =
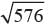 = 24 cm.
= 24 cm.How many tangents can a circle have?- a)1
- b)2
- c)4
- d)Infinite
Correct answer is option 'D'. Can you explain this answer?
How many tangents can a circle have?
a)
1
b)
2
c)
4
d)
Infinite
|
|
Priyanka Kapoor answered |
A tangent to a circle is a line that intersects the circle at only one point. On every point on the circle, one tangent can be drawn as shown in the figure below.
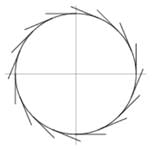
As per the above diagram, we see that a circle can have infinitely many tangents.

As per the above diagram, we see that a circle can have infinitely many tangents.
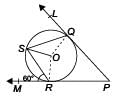
In the given figure, O is the centre of a circle; PQL and PRM are the tangents at the points Q and R respectively and S is a point on the circle such that ∠SQL = 50° and ∠SRM = 60°. Then, find ∠QSR and ∠RPQ.
- a)40°, 140°
- b)50°, 140°
- c)60°, 120°
- d)70°, 40°
Correct answer is option 'D'. Can you explain this answer?
In the given figure, O is the centre of a circle; PQL and PRM are the tangents at the points Q and R respectively and S is a point on the circle such that ∠SQL = 50° and ∠SRM = 60°. Then, find ∠QSR and ∠RPQ.


a)
40°, 140°
b)
50°, 140°
c)
60°, 120°
d)
70°, 40°
|
|
Ritu Saxena answered |
Since, PQL is a tangent and OQ is a radius, so ∠OQL = 90°
∴ ∠OQS = (90°- 50°) = 40°
Now, OQ = OS ⇒ ∠OSQ = ∠OQS = 40°
Similarly, ∠ORS = (90°- 60°) = 30°
And, OR = OS ⇒ ∠OSR = ∠ORS = 30°
∴ ∠QSR = ∠OSQ + ∠OSR = (40°+ 30°) = 70°
Now, ∠ROQ = 2 ∠QSR = 140°
∠ROQ + ∠ORP + ∠OQP + ∠RPQ = 360° (Angle sum property of quadrilateral QORP)
⇒ 140° + 90° + 90° + ∠RPQ = 360°
⇒ ∠RPQ = 40°
∴ ∠OQS = (90°- 50°) = 40°
Now, OQ = OS ⇒ ∠OSQ = ∠OQS = 40°
Similarly, ∠ORS = (90°- 60°) = 30°
And, OR = OS ⇒ ∠OSR = ∠ORS = 30°
∴ ∠QSR = ∠OSQ + ∠OSR = (40°+ 30°) = 70°
Now, ∠ROQ = 2 ∠QSR = 140°
∠ROQ + ∠ORP + ∠OQP + ∠RPQ = 360° (Angle sum property of quadrilateral QORP)
⇒ 140° + 90° + 90° + ∠RPQ = 360°
⇒ ∠RPQ = 40°
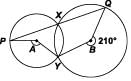
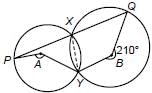
In the given figure, A and B are the centres of two circles that intersect at X and Y. PXQ is a straight line. If reflex angle QBY = 210°, find obtuse angle PAY.
- a)210°
- b)150°
- c)160°
- d)120°
Correct answer is option 'B'. Can you explain this answer?
In the given figure, A and B are the centres of two circles that intersect at X and Y. PXQ is a straight line. If reflex angle QBY = 210°, find obtuse angle PAY.


a)
210°
b)
150°
c)
160°
d)
120°
|
|
Ritu Saxena answered |
In quadrilateral YBQX
∠YXQ = 1/2 reflex ∠QBY = 1/2 x 210° = 105°
PQ is a straight line
⇒ ∠PXY + ∠YXQ = 180° (linear pair)
⇒ ∠PXY = 180°- 105° = 75°
Now, in quadrilateral PAYX
∠PXY = 1/2∠PAY ∴ ∠PAY = 2∠PXY = 150°
∠YXQ = 1/2 reflex ∠QBY = 1/2 x 210° = 105°
PQ is a straight line
⇒ ∠PXY + ∠YXQ = 180° (linear pair)
⇒ ∠PXY = 180°- 105° = 75°
Now, in quadrilateral PAYX
∠PXY = 1/2∠PAY ∴ ∠PAY = 2∠PXY = 150°

Chapter doubts & questions for Circles - Olympiad Preparation for Class 10 2025 is part of Class 10 exam preparation. The chapters have been prepared according to the Class 10 exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Class 10 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Circles - Olympiad Preparation for Class 10 in English & Hindi are available as part of Class 10 exam.
Download more important topics, notes, lectures and mock test series for Class 10 Exam by signing up for free.

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup

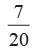 of the area of the circle, then what is the sector angle of the circle?
of the area of the circle, then what is the sector angle of the circle?