All Exams >
Class 6 >
Mathematics for Class 6 >
All Questions
All questions of Symmetry for Class 6 Exam
Which of these figures does not have rotational symmetry?- a)Equilateral Triangle
- b)Rectangle
- c)Circle
- d)Scalene Triangle
Correct answer is option 'D'. Can you explain this answer?
a)
Equilateral Triangle
b)
Rectangle
c)
Circle
d)
Scalene Triangle

|
Dr Manju Sen answered |
A scalene triangle has no rotational symmetry because none of its angles or sides are equal, so it does not look the same when rotated.
What happens when you fold a kite shape along its line of symmetry?- a)The two halves overlap perfectly
- b)The two halves do not overlap
- c)Only part of it overlaps
- d)The kite becomes a square
Correct answer is option 'A'. Can you explain this answer?
a)
The two halves overlap perfectly
b)
The two halves do not overlap
c)
Only part of it overlaps
d)
The kite becomes a square
|
|
Arjun Yadav answered |
When you fold a kite shape along its line of symmetry:
- The two halves overlap perfectly: When you fold a kite shape along its line of symmetry, the two halves will perfectly overlap each other. This is because a kite shape has a line of symmetry that divides it into two equal halves that are mirror images of each other. So, when you fold the kite along this line, the two halves will fit perfectly on top of each other.
- This is similar to folding a piece of paper in half along its center crease. The two halves of the paper will align perfectly, creating a mirror image of each other.
- Importance of symmetry: Symmetry is an important concept in mathematics and geometry. It helps us understand patterns, shapes, and structures in a more organized and systematic way. Folding a shape along its line of symmetry is one way to demonstrate this concept visually.
- Visual representation: To better understand this concept, you can try drawing a kite shape on a piece of paper and folding it along its line of symmetry. You will see that the two halves overlap perfectly, showing the symmetry of the shape.
- Conclusion: Folding a kite shape along its line of symmetry results in the two halves overlapping perfectly. This demonstrates the concept of symmetry and helps us visualize the mirror image relationship between the two halves of the shape.
- The two halves overlap perfectly: When you fold a kite shape along its line of symmetry, the two halves will perfectly overlap each other. This is because a kite shape has a line of symmetry that divides it into two equal halves that are mirror images of each other. So, when you fold the kite along this line, the two halves will fit perfectly on top of each other.
- This is similar to folding a piece of paper in half along its center crease. The two halves of the paper will align perfectly, creating a mirror image of each other.
- Importance of symmetry: Symmetry is an important concept in mathematics and geometry. It helps us understand patterns, shapes, and structures in a more organized and systematic way. Folding a shape along its line of symmetry is one way to demonstrate this concept visually.
- Visual representation: To better understand this concept, you can try drawing a kite shape on a piece of paper and folding it along its line of symmetry. You will see that the two halves overlap perfectly, showing the symmetry of the shape.
- Conclusion: Folding a kite shape along its line of symmetry results in the two halves overlapping perfectly. This demonstrates the concept of symmetry and helps us visualize the mirror image relationship between the two halves of the shape.
How many lines of symmetry does a square have?- a)1
- b)2
- c)4
- d)6
Correct answer is option 'C'. Can you explain this answer?
a)
1
b)
2
c)
4
d)
6

|
Shiksha Academy answered |
A square has 4 lines of symmetry, two diagonals, and two axes (horizontal and vertical) through its center.
What is the smallest angle of rotation that will map a square onto itself?- a)45°
- b)60°
- c)90°
- d)180°
Correct answer is option 'C'. Can you explain this answer?
a)
45°
b)
60°
c)
90°
d)
180°

|
Rahul Kumar answered |
A square has rotational symmetry at 90 degrees, which means it looks the same after a 90-degree rotation.
Which of the following shapes has rotational symmetry but no line of symmetry?- a)Circle
- b)Scalene Triangle
- c)Rectangle
- d)Parallelogram
Correct answer is option 'D'. Can you explain this answer?
a)
Circle
b)
Scalene Triangle
c)
Rectangle
d)
Parallelogram
|
|
Muskaan Chavan answered |
Understanding Rotational Symmetry
Rotational symmetry occurs when a shape can be rotated around a central point and still look the same at certain angles.
Shapes in the Options:
- Circle: A circle has infinite lines of symmetry and rotational symmetry at any angle.
- Scalene Triangle: A scalene triangle has no lines of symmetry and lacks rotational symmetry.
- Rectangle: A rectangle has two lines of symmetry and also has rotational symmetry (180 degrees).
- Parallelogram: A parallelogram has rotational symmetry (180 degrees) but typically has no lines of symmetry, especially when it is not a rectangle or rhombus.
Why Parallelograms Fit the Criteria:
- The parallelogram can be rotated 180 degrees and appear unchanged, demonstrating rotational symmetry.
- Lines of symmetry are defined as a line that divides a shape into two identical halves. A general parallelogram does not have such lines unless it is a special case (like a rectangle or rhombus).
Conclusion:
Thus, the correct answer is option 'D', as a parallelogram exemplifies a shape that possesses rotational symmetry without having any lines of symmetry. This unique characteristic sets it apart from the other options provided.
Rotational symmetry occurs when a shape can be rotated around a central point and still look the same at certain angles.
Shapes in the Options:
- Circle: A circle has infinite lines of symmetry and rotational symmetry at any angle.
- Scalene Triangle: A scalene triangle has no lines of symmetry and lacks rotational symmetry.
- Rectangle: A rectangle has two lines of symmetry and also has rotational symmetry (180 degrees).
- Parallelogram: A parallelogram has rotational symmetry (180 degrees) but typically has no lines of symmetry, especially when it is not a rectangle or rhombus.
Why Parallelograms Fit the Criteria:
- The parallelogram can be rotated 180 degrees and appear unchanged, demonstrating rotational symmetry.
- Lines of symmetry are defined as a line that divides a shape into two identical halves. A general parallelogram does not have such lines unless it is a special case (like a rectangle or rhombus).
Conclusion:
Thus, the correct answer is option 'D', as a parallelogram exemplifies a shape that possesses rotational symmetry without having any lines of symmetry. This unique characteristic sets it apart from the other options provided.
How many lines of symmetry does a regular hexagon have?- a)2
- b)3
- c)4
- d)6
Correct answer is option 'D'. Can you explain this answer?
a)
2
b)
3
c)
4
d)
6

|
Torcia Education answered |
A regular hexagon has 6 lines of symmetry, each line passing through opposite vertices or midpoints of opposite sides.
What happens when you rotate a regular pentagon by 72 degrees?- a)It looks the same
- b)It looks different
- c)It becomes a square
- d)It becomes a triangle
Correct answer is option 'A'. Can you explain this answer?
a)
It looks the same
b)
It looks different
c)
It becomes a square
d)
It becomes a triangle

|
EduRev Class 6 answered |
A regular pentagon has rotational symmetry at 72 degrees, so it looks the same after a 72-degree rotation.
Number of lines of symmetry in a rhombus is:- a)0
- b)1
- c)2
- d)4
Correct answer is option 'C'. Can you explain this answer?
Number of lines of symmetry in a rhombus is:
a)
0
b)
1
c)
2
d)
4
|
|
Sagnik Saha answered |
Understanding Lines of Symmetry
Lines of symmetry are imaginary lines that divide a shape into two identical halves, such that one half is a mirror image of the other.
Characteristics of a Rhombus
- A rhombus is a type of quadrilateral where all four sides are of equal length.
- The opposite angles of a rhombus are equal, and adjacent angles are supplementary.
Lines of Symmetry in a Rhombus
A rhombus has two lines of symmetry:
- Diagonal Symmetries: The two diagonals of the rhombus serve as lines of symmetry.
- When you draw a diagonal, it divides the rhombus into two congruent triangles.
- Each triangle is a mirror image of the other.
- Identifying the Diagonals:
- One diagonal runs from one vertex to the opposite vertex.
- The second diagonal crosses the first and runs from the other two vertices.
Visualizing the Symmetry
- If you fold the rhombus along either of its diagonals, the two halves will align perfectly.
- This property shows that there are indeed two lines of symmetry in a rhombus.
Conclusion
In conclusion, the correct answer to the question regarding the number of lines of symmetry in a rhombus is option 'C', which states that there are 2 lines of symmetry. Understanding this concept is essential in geometry, especially when studying polygons and their properties.
Lines of symmetry are imaginary lines that divide a shape into two identical halves, such that one half is a mirror image of the other.
Characteristics of a Rhombus
- A rhombus is a type of quadrilateral where all four sides are of equal length.
- The opposite angles of a rhombus are equal, and adjacent angles are supplementary.
Lines of Symmetry in a Rhombus
A rhombus has two lines of symmetry:
- Diagonal Symmetries: The two diagonals of the rhombus serve as lines of symmetry.
- When you draw a diagonal, it divides the rhombus into two congruent triangles.
- Each triangle is a mirror image of the other.
- Identifying the Diagonals:
- One diagonal runs from one vertex to the opposite vertex.
- The second diagonal crosses the first and runs from the other two vertices.
Visualizing the Symmetry
- If you fold the rhombus along either of its diagonals, the two halves will align perfectly.
- This property shows that there are indeed two lines of symmetry in a rhombus.
Conclusion
In conclusion, the correct answer to the question regarding the number of lines of symmetry in a rhombus is option 'C', which states that there are 2 lines of symmetry. Understanding this concept is essential in geometry, especially when studying polygons and their properties.
Which one of the following figures has infinitely many lines of symmetry?- a)Pentagon
- b)Hexagon
- c)Circle
- d)Line Segment
Correct answer is option 'C'. Can you explain this answer?
Which one of the following figures has infinitely many lines of symmetry?
a)
Pentagon
b)
Hexagon
c)
Circle
d)
Line Segment
|
|
Kiran Das answered |
Understanding Lines of Symmetry
Lines of symmetry are defined as imaginary lines that divide a shape into two identical halves that are mirror images of each other.
Types of Figures Analyzed
- Pentagon: A regular pentagon has 5 lines of symmetry, while an irregular pentagon may have fewer or none.
- Hexagon: A regular hexagon has 6 lines of symmetry. Like the pentagon, irregular hexagons may have fewer lines.
- Circle: A circle has an infinite number of lines of symmetry. Any line drawn through the center of a circle divides it into two equal halves.
- Line Segment: A line segment has only one line of symmetry, which is the line that bisects it.
Why the Circle Has Infinite Lines of Symmetry
- Every Diameter Counts: Any line that passes through the center of the circle acts as a line of symmetry. This includes horizontal, vertical, and diagonal lines.
- Uniformity: The circular shape is uniform in all directions, meaning that no matter where you draw a line through the center, both halves will always look identical.
- Contrast with Other Shapes: Unlike polygons (pentagon and hexagon) that have a limited number of sides, a circle can have a line of symmetry at every angle, leading to infinity.
Conclusion
In summary, out of the given options, the circle stands out as the only figure with infinitely many lines of symmetry, making option 'C' the correct answer.
Lines of symmetry are defined as imaginary lines that divide a shape into two identical halves that are mirror images of each other.
Types of Figures Analyzed
- Pentagon: A regular pentagon has 5 lines of symmetry, while an irregular pentagon may have fewer or none.
- Hexagon: A regular hexagon has 6 lines of symmetry. Like the pentagon, irregular hexagons may have fewer lines.
- Circle: A circle has an infinite number of lines of symmetry. Any line drawn through the center of a circle divides it into two equal halves.
- Line Segment: A line segment has only one line of symmetry, which is the line that bisects it.
Why the Circle Has Infinite Lines of Symmetry
- Every Diameter Counts: Any line that passes through the center of the circle acts as a line of symmetry. This includes horizontal, vertical, and diagonal lines.
- Uniformity: The circular shape is uniform in all directions, meaning that no matter where you draw a line through the center, both halves will always look identical.
- Contrast with Other Shapes: Unlike polygons (pentagon and hexagon) that have a limited number of sides, a circle can have a line of symmetry at every angle, leading to infinity.
Conclusion
In summary, out of the given options, the circle stands out as the only figure with infinitely many lines of symmetry, making option 'C' the correct answer.
Which shape will look the same after being rotated by 180 degrees on the vertical axis?- a)Letters like 'F', 'L', 'P', 'R'
- b)Equilateral Triangle
- c)Numbers like 4, 5, 6
- d)None of the above
Correct answer is option 'B'. Can you explain this answer?
Which shape will look the same after being rotated by 180 degrees on the vertical axis?
a)
Letters like 'F', 'L', 'P', 'R'
b)
Equilateral Triangle
c)
Numbers like 4, 5, 6
d)
None of the above
|
|
Devika Basak answered |
Understanding Rotation Symmetry
In geometry, rotation symmetry refers to how a shape looks after being turned around a central point. For a shape to look the same after being rotated 180 degrees, it must have a specific symmetry.
Evaluating Each Option
Conclusion
The correct answer is option B, the equilateral triangle. Its symmetrical properties allow it to remain unchanged when rotated 180 degrees, making it a perfect example of rotational symmetry. The other options lack this characteristic, confirming that only the equilateral triangle fits the criteria.
In geometry, rotation symmetry refers to how a shape looks after being turned around a central point. For a shape to look the same after being rotated 180 degrees, it must have a specific symmetry.
Evaluating Each Option
- Option A: Letters like F, L, P, R
- These letters do not maintain their appearance when rotated 180 degrees.
- Option B: Equilateral Triangle
- When an equilateral triangle is rotated 180 degrees, it still looks the same. This is because all sides and angles are equal, allowing for rotational symmetry.
- Option C: Numbers like 4, 5, 6
- These numbers change their appearance when rotated 180 degrees. For example, the number 5 becomes unrecognizable and the number 6 looks like a 9.
- Option D: None of the above
- This option is incorrect since the equilateral triangle does have the desired rotational symmetry.
Conclusion
The correct answer is option B, the equilateral triangle. Its symmetrical properties allow it to remain unchanged when rotated 180 degrees, making it a perfect example of rotational symmetry. The other options lack this characteristic, confirming that only the equilateral triangle fits the criteria.
If a circle is folded along any diameter, what happens?- a)The two halves overlap perfectly
- b)The two halves do not overlap
- c)The circle’s size decreases
- d)The circle becomes a semicircle
Correct answer is option 'A'. Can you explain this answer?
a)
The two halves overlap perfectly
b)
The two halves do not overlap
c)
The circle’s size decreases
d)
The circle becomes a semicircle

|
Dr Manju Sen answered |
A circle has an infinite number of lines of symmetry, so folding along any diameter will cause the two halves to overlap perfectly.
How many lines of symmetry does an equilateral triangle have?- a)1
- b)2
- c)3
- d)0
Correct answer is option 'C'. Can you explain this answer?
a)
1
b)
2
c)
3
d)
0

|
Rahul Kumar answered |
An equilateral triangle has 3 lines of symmetry, each passing through a vertex and the midpoint of the opposite side.
What is the smallest angle of rotation that maps a regular hexagon onto itself?- a)30°
- b)60°
- c)90°
- d)120°
Correct answer is option 'B'. Can you explain this answer?
a)
30°
b)
60°
c)
90°
d)
120°

|
Coachify answered |
The smallest angle of rotation that maps a regular hexagon onto itself is 60 degrees, corresponding to its order of rotational symmetry.
What is the order of rotational symmetry of a regular pentagon?- a)1
- b)2
- c)5
- d)3
Correct answer is option 'C'. Can you explain this answer?
a)
1
b)
2
c)
5
d)
3

|
Torcia Education answered |
The order of rotational symmetry of a regular pentagon is 5, meaning it can be rotated by 72°, 144°, 216°, 288°, and 360° to look the same.
How many lines of symmetry does a regular octagon have?- a)4
- b)5
- c)8
- d)6
Correct answer is option 'C'. Can you explain this answer?
a)
4
b)
5
c)
8
d)
6

|
Torcia Education answered |
A regular octagon has 8 lines of symmetry, one for each vertex and the midpoint of the opposite side.
Which shape has only one line of symmetry?- a)Square
- b)Rectangle
- c)Circle
- d)Isosceles Triangle
Correct answer is option 'D'. Can you explain this answer?
a)
Square
b)
Rectangle
c)
Circle
d)
Isosceles Triangle

|
Coachify answered |
An isosceles triangle has only one line of symmetry that passes through its vertex and the midpoint of the base.
How many lines of symmetry does a regular pentagon have? 
- a)1
- b)2
- c)5
- d)3
Correct answer is option 'C'. Can you explain this answer?
How many lines of symmetry does a regular pentagon have?

a)
1
b)
2
c)
5
d)
3

|
Shiksha Academy answered |
A regular pentagon has 5 lines of symmetry, one for each vertex and the midpoint of the opposite side.
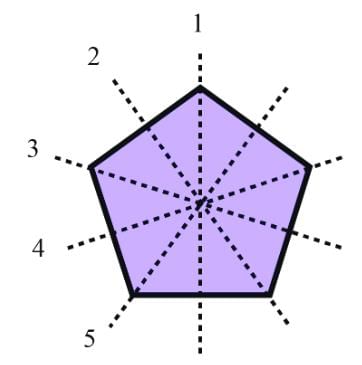
In a regular polygon of n sides, the number of lines of symmetry is:- a)0
- b)1
- c)n
- d)an infinite number
Correct answer is option 'C'. Can you explain this answer?
In a regular polygon of n sides, the number of lines of symmetry is:
a)
0
b)
1
c)
n
d)
an infinite number

|
Praveen Kumar answered |
In a regular polygon with n sides, the number of lines of symmetry is n. This is because a regular polygon has as many lines of symmetry as it has sides, with each line of symmetry passing through a vertex and the midpoint of the opposite side (or through the midpoints of opposite sides in some cases).
The correct answer is (c) n.
Which of the following shapes has no lines of symmetry?- a)Scalene Triangle
- b)Square
- c)Rectangle
- d)Regular Pentagon
Correct answer is option 'A'. Can you explain this answer?
a)
Scalene Triangle
b)
Square
c)
Rectangle
d)
Regular Pentagon

|
Dr Manju Sen answered |
A scalene triangle has no lines of symmetry because all its sides and angles are different.
What happens when you rotate a square by 90 degrees?- a)It looks the same
- b)It looks different
- c)It turns into a rectangle
- d)It becomes smaller
Correct answer is option 'A'. Can you explain this answer?
a)
It looks the same
b)
It looks different
c)
It turns into a rectangle
d)
It becomes smaller

|
Rahul Kumar answered |
A square looks the same after being rotated by 90 degrees because it has rotational symmetry at this angle.
Chapter doubts & questions for Symmetry - Mathematics for Class 6 2025 is part of Class 6 exam preparation. The chapters have been prepared according to the Class 6 exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Class 6 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Symmetry - Mathematics for Class 6 in English & Hindi are available as part of Class 6 exam.
Download more important topics, notes, lectures and mock test series for Class 6 Exam by signing up for free.
Mathematics for Class 6
48 videos|374 docs|23 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup









