All Exams >
Electronics and Communication Engineering (ECE) >
Digital Signal Processing >
All Questions
All questions of Introduction to Digital Signal Processing for Electronics and Communication Engineering (ECE) Exam
What is the spectrum that is obtained when we plot |ck |2 as a function of frequencies kF0, k=0,±1,±2..?- a)Average power spectrum
- b)Energy spectrum
- c)Power density spectrum
- d)None of the mentioned
Correct answer is option 'C'. Can you explain this answer?
What is the spectrum that is obtained when we plot |ck |2 as a function of frequencies kF0, k=0,±1,±2..?
a)
Average power spectrum
b)
Energy spectrum
c)
Power density spectrum
d)
None of the mentioned
|
|
Ravi Singh answered |
Explanation: When we plot a graph of |ck |2 as a function of frequencies kF0, k=0,±1,±2… the following spectrum is obtained which is known as Power density spectrum.
Determine the output y(n) of a LTI system with impulse response h(n)=anu(n),|a|<1with the input sequence x(n)=u(n). - a)(1-a(n+1))/(1-a)
- b)(1-a(n-1))/(1-a)
- c)(1+a(n+1))/(1+a)
- d)None of the mentioned
Correct answer is option 'A'. Can you explain this answer?
Determine the output y(n) of a LTI system with impulse response h(n)=anu(n),|a|<1with the input sequence x(n)=u(n).
a)
(1-a(n+1))/(1-a)
b)
(1-a(n-1))/(1-a)
c)
(1+a(n+1))/(1+a)
d)
None of the mentioned
|
|
Subhankar Goyal answered |
Explanation: Now fold the signal x(n) and shift it by one unit at a time and sum as follows
y(0)=x(0)h(0)=1
y(1)=h(0)x(1)+h(1)x(0)=1.1+a.1=1+a
y(2)=h(0)x(2)+h(1)x(1)+h(2)x(0)=1.1+a.1+a2.1=1+a+a2
Similarly, y(n)=1+a+a2+….an= (1-a(n+1))/(1-a).
y(0)=x(0)h(0)=1
y(1)=h(0)x(1)+h(1)x(0)=1.1+a.1=1+a
y(2)=h(0)x(2)+h(1)x(1)+h(2)x(0)=1.1+a.1+a2.1=1+a+a2
Similarly, y(n)=1+a+a2+….an= (1-a(n+1))/(1-a).
What is the zero-input response of the system described by the homogenous second order equation y(n)-3y(n-1)-4y(n-2)=0 if the initial conditions are y(-1)=5 and y(-2)=0? - a)(-1)n-1 + (4)n-2
- b)(-1)n+1 + (4)n+2
- c)(-1)n+1 + (4)n-2
- d)None of the mentioned
Correct answer is option 'B'. Can you explain this answer?
What is the zero-input response of the system described by the homogenous second order equation y(n)-3y(n-1)-4y(n-2)=0 if the initial conditions are y(-1)=5 and y(-2)=0?
a)
(-1)n-1 + (4)n-2
b)
(-1)n+1 + (4)n+2
c)
(-1)n+1 + (4)n-2
d)
None of the mentioned
|
|
Tushar Unni answered |
Explanation: Given difference equation is y(n)-3y(n-1)-4y(n-2)=0—-(1)
Let y(n)=λn
Substituting y(n) in the given equation
=> λn – 3λn-1 – 4λn-2 = 0
=> λn-2(λ2 – 3λ – 4) = 0
the roots of the above equation are λ=-1,4
Therefore, general form of the solution of the homogenous equation is
Let y(n)=λn
Substituting y(n) in the given equation
=> λn – 3λn-1 – 4λn-2 = 0
=> λn-2(λ2 – 3λ – 4) = 0
the roots of the above equation are λ=-1,4
Therefore, general form of the solution of the homogenous equation is
The zero-input response of the system can be calculated from the homogenous solution by evaluating the constants in the above equation, given the initial conditions y(-1) and y(-2).
From the given equation (1)
y(0)=3y(-1)+4y(-2)
y(1)=3y(0)+4y(-1)
=3[3y(-1)+4y(-2)]+4y(-1)
=13y(-1)+12y(-2)
From the equation (2)
y(0)=C1+C2 and
y(1)=C1(-1)+C2(4)=-C1+4C2
By equating these two set of relations, we have
C1+C2=3y(-1)+4y(-2)=15
-C1+4C2=13y(-1)+12y(-2)=65
On solving the above two equations we get C1=-1 and C2=16
Therefore the zero-input response is Yzi(n) = (-1)n+1 + (4)n+2.
From the given equation (1)
y(0)=3y(-1)+4y(-2)
y(1)=3y(0)+4y(-1)
=3[3y(-1)+4y(-2)]+4y(-1)
=13y(-1)+12y(-2)
From the equation (2)
y(0)=C1+C2 and
y(1)=C1(-1)+C2(4)=-C1+4C2
By equating these two set of relations, we have
C1+C2=3y(-1)+4y(-2)=15
-C1+4C2=13y(-1)+12y(-2)=65
On solving the above two equations we get C1=-1 and C2=16
Therefore the zero-input response is Yzi(n) = (-1)n+1 + (4)n+2.
What is the one sided z-transform X+(z) of the signal x(n)={1,2,5,7,0,1}? - a)z2+2z+5+7z-1+z-3
- b)5+7z+z3
- c)z-2+2z-1+5+7z+z3
- d)5+7z-1+z-3
Correct answer is option 'D'. Can you explain this answer?
What is the one sided z-transform X+(z) of the signal x(n)={1,2,5,7,0,1}?
a)
z2+2z+5+7z-1+z-3
b)
5+7z+z3
c)
z-2+2z-1+5+7z+z3
d)
5+7z-1+z-3
|
|
Navya Iyer answered |
Explanation: Since the one sided z-transform is valid only for n>=0, the z-transform of the given signal will be X+(z)= 5+7z-1+z-3.
What is the Fourier transform of the signal x(n)=a|n|, |a|<1? - a)(1+a2)/(1-2acosω+a2)
- b)(1-a2)/(1-2acosω+a2)
- c)2a/(1-2acosω+a2 )
- d)None of the mentioned
Correct answer is option 'B'. Can you explain this answer?
What is the Fourier transform of the signal x(n)=a|n|, |a|<1?
a)
(1+a2)/(1-2acosω+a2)
b)
(1-a2)/(1-2acosω+a2)
c)
2a/(1-2acosω+a2 )
d)
None of the mentioned
|
|
Arindam Malik answered |
Explanation: First we observe x(n) can be expressed as
x(n)=x1(n)+x2(n)
where x1(n)= an, n>0
=0, elsewhere
x(n)=x1(n)+x2(n)
where x1(n)= an, n>0
=0, elsewhere
x2(n)=a-n, n<0 =0, elsewhere Now applying Fourier transform for the above two signals, we get X1(ω)= 1/(1-aejω)/((1-ae(-jω) )(1-aejω)) = (1-acosω-jasinω)/(1-2acosω+a2 )
Now, X(ω)= X1(ω)+ X2(ω)= 1/(1-ae^(-jω) )+(ae^jω)/(1-ae^jω ) = (1-a2)/(1-2acosω+a2).
If the output of the system of the system at any ‘n’ depends only the present or the past values of the inputs then the system is said to be:- a)Linear
- b)Non-Linear
- c)Causal
- d)Non-causal
Correct answer is option 'C'. Can you explain this answer?
If the output of the system of the system at any ‘n’ depends only the present or the past values of the inputs then the system is said to be:
a)
Linear
b)
Non-Linear
c)
Causal
d)
Non-causal
|
|
Tejas Ghoshal answered |
Explanation: A system is said to be causal if the output of the system is defined as the function shown below
y(n)=F[x(n),x(n-1),x(n-2),…] So, according to the conditions given in the question, the system is a causal system.
y(n)=F[x(n),x(n-1),x(n-2),…] So, according to the conditions given in the question, the system is a causal system.
What is the particular solution of the first order difference equation y(n)+ay(n-1)=x(n) where |a|<1, when the input of the system x(n)=u(n)?- a)1/(1+a) u(n)
- b)1/(1-a) u(n)
- c)1/(1+a)
- d)1/(1-a)
Correct answer is option 'A'. Can you explain this answer?
What is the particular solution of the first order difference equation y(n)+ay(n-1)=x(n) where |a|<1, when the input of the system x(n)=u(n)?
a)
1/(1+a) u(n)
b)
1/(1-a) u(n)
c)
1/(1+a)
d)
1/(1-a)
|
|
Rishabh Sharma answered |
Explanation: The assumed solution of the difference equation to the forcing equation x(n), called the particular solution of the difference equation is
yp(n)=Kx(n)=Ku(n) (where K is a scale factor)
Substitute the above equation in the given equation
=>Ku(n)+aKu(n-1)=u(n)
To determine K we must evaluate the above equation for any n>=1, so that no term vanishes.
=> K+aK=1
=>K=1/(1+a)
Therefore the particular solution is yp(n)= 1/(1+a) u(n).
yp(n)=Kx(n)=Ku(n) (where K is a scale factor)
Substitute the above equation in the given equation
=>Ku(n)+aKu(n-1)=u(n)
To determine K we must evaluate the above equation for any n>=1, so that no term vanishes.
=> K+aK=1
=>K=1/(1+a)
Therefore the particular solution is yp(n)= 1/(1+a) u(n).
What is the impulse response of the system described by the second order difference equation y(n)-3y(n-1)-4y(n-2)=x(n)+2x(n-1)? - a)[-1/5 (-1)n-6/5 (4)n]u(n)
- b)[1/5 (-1)n – 6/5 (4)n]u(n)
- c)[ 1/5 (-1)n+ 6/5 (4)n]u(n)
- d)[- 1/5 (-1)n+ 6/5 (4)n]u(n)
Correct answer is option 'D'. Can you explain this answer?
What is the impulse response of the system described by the second order difference equation y(n)-3y(n-1)-4y(n-2)=x(n)+2x(n-1)?
a)
[-1/5 (-1)n-6/5 (4)n]u(n)
b)
[1/5 (-1)n – 6/5 (4)n]u(n)
c)
[ 1/5 (-1)n+ 6/5 (4)n]u(n)
d)
[- 1/5 (-1)n+ 6/5 (4)n]u(n)
|
|
Nishanth Mehta answered |
Explanation: The homogenous solution of the given equation is yh(n)=C1(-1)n+C2(4)n—-(1)
To find the impulse response, x(n)=δ(n)
now, for n=0 and n=1 we get
y(0)=1 and
y(1)=3+2=5
From equation (1) we get
y(0)=C1+C2 and
y(1)=-C1+4C2
On solving the above two set of equations we get
C1=- 1/5 and C2= 6/5
=>h(n)= [-1/5 (-1)n + 6/5 (4)n]u(n).
To find the impulse response, x(n)=δ(n)
now, for n=0 and n=1 we get
y(0)=1 and
y(1)=3+2=5
From equation (1) we get
y(0)=C1+C2 and
y(1)=-C1+4C2
On solving the above two set of equations we get
C1=- 1/5 and C2= 6/5
=>h(n)= [-1/5 (-1)n + 6/5 (4)n]u(n).
What is the relation between cross correlation and auto correlation? - a)|rxy(l)|=√(rxx(0).ryy(0))
- b)|rxy(l)|≥√(rxx(0).ryy(0))
- c)|rxy(l)|≠√(rxx(0).ryy(0))
- d)|rxy(l)|≤√(rxx(0).ryy(0))
Correct answer is option 'D'. Can you explain this answer?
What is the relation between cross correlation and auto correlation?
a)
|rxy(l)|=√(rxx(0).ryy(0))
b)
|rxy(l)|≥√(rxx(0).ryy(0))
c)
|rxy(l)|≠√(rxx(0).ryy(0))
d)
|rxy(l)|≤√(rxx(0).ryy(0))
|
|
Pranab Banerjee answered |
Explanation:
We know that, a2rxx(0)+b2ryy(0)+2abrxy(l) ≥0
=> (a/b)2rxx(0)+ryy(0)+2(a/b)rxy(l) ≥0
Since the quadratic is nonnegative, it follows that the discriminate of this quadratic must be non positive, that is 4[r2xy(l)- rxx(0) ryy(0)] ≤0 =>|rxy(l)|≤√(rxx(0).ryy(0)).
We know that, a2rxx(0)+b2ryy(0)+2abrxy(l) ≥0
=> (a/b)2rxx(0)+ryy(0)+2(a/b)rxy(l) ≥0
Since the quadratic is nonnegative, it follows that the discriminate of this quadratic must be non positive, that is 4[r2xy(l)- rxx(0) ryy(0)] ≤0 =>|rxy(l)|≤√(rxx(0).ryy(0)).
If a system do not have a bounded output for bounded input, then the system is said to be:- a)Causal
- b)Non-causal
- c)Stable
- d)Non-stable
Correct answer is option 'D'. Can you explain this answer?
If a system do not have a bounded output for bounded input, then the system is said to be:
a)
Causal
b)
Non-causal
c)
Stable
d)
Non-stable
|
|
Abhijeet Mehta answered |
Explanation: An arbitrary relaxed system is said to be BIBO stable if it has a bounded output for every value in the bounded input. So, the system given in the question is a Non-stable system.
x(n)*δ(n-n0)= - a)x(n+n0)
- b)x(n-n0)
- c)x(-n-n0)
- d)x(-n+n0)
Correct answer is option 'B'. Can you explain this answer?
x(n)*δ(n-n0)=
a)
x(n+n0)
b)
x(n-n0)
c)
x(-n-n0)
d)
x(-n+n0)
|
|
Rajesh Saha answered |
It seems like your message got cut off. Could you please provide more information or complete your question?
What is the ROC of the signal x(n)=δ(n-k),k>0?- a)z=0
- b)z=∞
- c)Entire z-plane, except at z=0
- d)Entire z-plane, except at z=∞
Correct answer is option 'C'. Can you explain this answer?
What is the ROC of the signal x(n)=δ(n-k),k>0?
a)
z=0
b)
z=∞
c)
Entire z-plane, except at z=0
d)
Entire z-plane, except at z=∞
|
|
Rashi Banerjee answered |
Explanation: We know that, the z-transform of a signal x(n) is 
Given x(n)= δ(n-k)=1 at n=k
=> X(z)=z-k
From the above equation, X(z) is defined at all values of z except at z=0 for k>0.
So ROC is defined as Entire z-plane, except at z=0.
Given x(n)= δ(n-k)=1 at n=k
=> X(z)=z-k
From the above equation, X(z) is defined at all values of z except at z=0 for k>0.
So ROC is defined as Entire z-plane, except at z=0.
If a signal x(t) is processed through a system to obtain the signal (x(t)2), then the system is said to be:- a)Linear
- b)Non-linear
- c)Exponential
- d)None of the mentioned
Correct answer is option 'B'. Can you explain this answer?
If a signal x(t) is processed through a system to obtain the signal (x(t)2), then the system is said to be:
a)
Linear
b)
Non-linear
c)
Exponential
d)
None of the mentioned
|
|
Rahul Chavan answered |
Explanation: Let the input signal be ‘t’. Then the output signal after passing through the system is y=t2 which is the equation of a parabola. So, the system is non-linear.
If x(n)=(0,1,2,3,3,0,0,0) then x(2n) is:- a)(0,2,4,6,6,0,0,0)
- b)(0,1,2,3,3,0,0,0)
- c)(0,2,3,0,0,0,0,0)
- d)None of the mentioned
Correct answer is option 'C'. Can you explain this answer?
If x(n)=(0,1,2,3,3,0,0,0) then x(2n) is:
a)
(0,2,4,6,6,0,0,0)
b)
(0,1,2,3,3,0,0,0)
c)
(0,2,3,0,0,0,0,0)
d)
None of the mentioned
|
|
Rahul Chavan answered |
Explanation: Substitute n=0,1,2… in x(2n) and obtain the values from the given x(n).
If x(n)=(0,0,1,2,3,4,0,0) then x(n-2) is:- a)(0,0,2,4,6,8,0,0)
- b)(0,0,1,2,3,4,0,0)
- c)(1,2,3,4,0,0,0,0)
- d)(0,0,0,0,1,2,3,4)
Correct answer is option 'D'. Can you explain this answer?
If x(n)=(0,0,1,2,3,4,0,0) then x(n-2) is:
a)
(0,0,2,4,6,8,0,0)
b)
(0,0,1,2,3,4,0,0)
c)
(1,2,3,4,0,0,0,0)
d)
(0,0,0,0,1,2,3,4)
|
|
Yashvi Das answered |
Explanation: The signal x(n) is shifted right by 2.
If the ROC of X(z) is r1<|z|<r2, then what is the ROC of X(a-1z)? - a)|a|r1<|z|<|a|r2
- b)|a|r1>|z|>|a|r2
- c)|a|r1<|z|>|a|r2
- d)|a|r1>|z|<|a|r2
Correct answer is option 'A'. Can you explain this answer?
If the ROC of X(z) is r1<|z|<r2, then what is the ROC of X(a-1z)?
a)
|a|r1<|z|<|a|r2
b)
|a|r1>|z|>|a|r2
c)
|a|r1<|z|>|a|r2
d)
|a|r1>|z|<|a|r2
|
|
Raj Desai answered |
If the ROC (Region of Convergence) of X(z) is r1, it means that the Z-transform X(z) converges for all values of z within the region r1. In other words, r1 represents the set of values for which the Z-transform of a discrete-time signal X(n) converges.
The ROC can have different shapes, depending on the properties of the signal X(n). It can be a circular region, an annular region, or extend to infinity. The choice of r1 determines the convergence properties of the Z-transform and is important for analyzing and manipulating the signal in the Z-domain.
It is worth noting that the ROC is typically specified as a range of values, such as |z| > r1 or r1 < |z|="" />< r2,="" where="" r1="" and="" r2="" represent="" the="" radius="" of="" convergence.="" r2,="" where="" r1="" and="" r2="" represent="" the="" radius="" of="" />
The ROC can have different shapes, depending on the properties of the signal X(n). It can be a circular region, an annular region, or extend to infinity. The choice of r1 determines the convergence properties of the Z-transform and is important for analyzing and manipulating the signal in the Z-domain.
It is worth noting that the ROC is typically specified as a range of values, such as |z| > r1 or r1 < |z|="" />< r2,="" where="" r1="" and="" r2="" represent="" the="" radius="" of="" convergence.="" r2,="" where="" r1="" and="" r2="" represent="" the="" radius="" of="" />
The normalized auto correlation ρxx(l) is defined as: - a)(rxx (l))/(rxx (0))
- b)-(rxx (l))/(rxx (0))
- c)(rxx (l))/(rxy (0))
- d)None of the mentioned
Correct answer is option 'A'. Can you explain this answer?
The normalized auto correlation ρxx(l) is defined as:
a)
(rxx (l))/(rxx (0))
b)
-(rxx (l))/(rxx (0))
c)
(rxx (l))/(rxy (0))
d)
None of the mentioned
|
|
Mayank Sengupta answered |
The normalized auto-correlation is a statistical measure that describes the degree of similarity between a signal and a delayed version of itself. It is a normalized version of the auto-correlation function, which is a measure of the correlation between two signals as a function of the time lag between them.
The normalized auto-correlation is often used in signal processing and time-series analysis to identify patterns and relationships between data points. It is typically calculated by dividing the auto-correlation function by the product of the standard deviations of the two signals being compared.
The resulting value ranges from -1 to 1, with a value of 1 indicating perfect correlation, 0 indicating no correlation, and -1 indicating perfect anti-correlation. A high value of normalized auto-correlation indicates that there is a strong relationship between the two signals, while a low value suggests the opposite.
The normalized auto-correlation is often used in signal processing and time-series analysis to identify patterns and relationships between data points. It is typically calculated by dividing the auto-correlation function by the product of the standard deviations of the two signals being compared.
The resulting value ranges from -1 to 1, with a value of 1 indicating perfect correlation, 0 indicating no correlation, and -1 indicating perfect anti-correlation. A high value of normalized auto-correlation indicates that there is a strong relationship between the two signals, while a low value suggests the opposite.
If the sampling rate Fs satisfies the sampling theorem, then the relation between quantization errors of analog signal(eq(t)) and discrete-time signal(eq(n)) is:- a)eq(t)=eq(n)
- b)eq(t)<eq(n)
- c)eq(t)>eq(n)
- d)not related
Correct answer is option 'A'. Can you explain this answer?
If the sampling rate Fs satisfies the sampling theorem, then the relation between quantization errors of analog signal(eq(t)) and discrete-time signal(eq(n)) is:
a)
eq(t)=eq(n)
b)
eq(t)<eq(n)
c)
eq(t)>eq(n)
d)
not related
|
|
Bibek Chakraborty answered |
Explanation: If it obeys sampling theorem, then the only error in A/D conversion is quantization error. So, the error is same for both analog and discrete-time signal.
What is the inverse z-transform of X(z)= 1/(1-1.5z-1+0.5z-2 ) if ROC is |z|<0.5? - a)[-2-0.5n]u(n)
- b)[-2+0.5n]u(n)
- c)[-2+0.5n]u(-n-1)
- d)[-2-0.5n]u(-n-1)
Correct answer is option 'C'. Can you explain this answer?
What is the inverse z-transform of X(z)= 1/(1-1.5z-1+0.5z-2 ) if ROC is |z|<0.5?
a)
[-2-0.5n]u(n)
b)
[-2+0.5n]u(n)
c)
[-2+0.5n]u(-n-1)
d)
[-2-0.5n]u(-n-1)
|
|
Gargi Sarkar answered |
Explanation: The partial fraction expansion for the given X(z) is
X(z)= 2z/(z-1)-z/(z-0.5)
In case when ROC is |z|<0.5,the signal is anti causal. Thus both the terms in the above equation are anti causal terms. So, if we apply inverse z-transform to the above equation we get x(n)= [-2+0.5n]u(-n-1).
X(z)= 2z/(z-1)-z/(z-0.5)
In case when ROC is |z|<0.5,the signal is anti causal. Thus both the terms in the above equation are anti causal terms. So, if we apply inverse z-transform to the above equation we get x(n)= [-2+0.5n]u(-n-1).
If W4100=Wx200, then what is the value of x?- a)2
- b)4
- c)8
- d)16
Correct answer is option 'C'. Can you explain this answer?
If W4100=Wx200, then what is the value of x?
a)
2
b)
4
c)
8
d)
16
|
|
Anisha Ahuja answered |
Explanation: We know that according to the periodicity and symmetry property,
100/4=200/x=>x=8.
100/4=200/x=>x=8.
Which of the following has to be performed in sampling rate conversion by rational factor?- a)Interpolation
- b)Decimation
- c)Either interpolation or decimation
- d)None of the mentioned
Correct answer is option 'A'. Can you explain this answer?
Which of the following has to be performed in sampling rate conversion by rational factor?
a)
Interpolation
b)
Decimation
c)
Either interpolation or decimation
d)
None of the mentioned
|
|
Dipika Basak answered |
The answer is option 'A' (Interpolation).
Interpolation is the process of increasing the sampling rate of a signal. It involves adding new samples between existing samples to create a higher-resolution representation of the signal. In sampling rate conversion by a rational factor, the sampling rate is changed by a rational number, which can be expressed as a ratio of two integers.
Sampling Rate Conversion:
Sampling rate conversion refers to the process of changing the sampling rate of a discrete-time signal. It is often necessary when combining or processing signals with different sampling rates, or when converting between analog and digital domains.
Rational Factor:
A rational factor is a ratio of two integers, where the numerator represents the new sampling rate and the denominator represents the original sampling rate. For example, if the original sampling rate is 100 Hz and the desired sampling rate is 200 Hz, the rational factor would be 2/1.
Interpolation:
Interpolation is the process of estimating new samples between existing samples. In the context of sampling rate conversion, interpolation is used to increase the sampling rate by inserting additional samples. These additional samples are computed using mathematical techniques such as linear interpolation, polynomial interpolation, or spline interpolation.
Decimation:
Decimation, on the other hand, is the process of reducing the sampling rate of a signal. It involves removing samples from the original signal to create a lower-resolution representation. Decimation is not performed in sampling rate conversion by a rational factor.
Sampling Rate Conversion by Rational Factor:
In sampling rate conversion by a rational factor, interpolation is always performed to increase the sampling rate. The interpolation factor is equal to the numerator of the rational factor. For example, if the rational factor is 2/1, the interpolation factor is 2.
Decimation, on the other hand, is only performed when the rational factor is less than 1. In such cases, the decimation factor is equal to the denominator of the rational factor.
Therefore, in the given options, only interpolation (option 'A') needs to be performed in sampling rate conversion by a rational factor.
Interpolation is the process of increasing the sampling rate of a signal. It involves adding new samples between existing samples to create a higher-resolution representation of the signal. In sampling rate conversion by a rational factor, the sampling rate is changed by a rational number, which can be expressed as a ratio of two integers.
Sampling Rate Conversion:
Sampling rate conversion refers to the process of changing the sampling rate of a discrete-time signal. It is often necessary when combining or processing signals with different sampling rates, or when converting between analog and digital domains.
Rational Factor:
A rational factor is a ratio of two integers, where the numerator represents the new sampling rate and the denominator represents the original sampling rate. For example, if the original sampling rate is 100 Hz and the desired sampling rate is 200 Hz, the rational factor would be 2/1.
Interpolation:
Interpolation is the process of estimating new samples between existing samples. In the context of sampling rate conversion, interpolation is used to increase the sampling rate by inserting additional samples. These additional samples are computed using mathematical techniques such as linear interpolation, polynomial interpolation, or spline interpolation.
Decimation:
Decimation, on the other hand, is the process of reducing the sampling rate of a signal. It involves removing samples from the original signal to create a lower-resolution representation. Decimation is not performed in sampling rate conversion by a rational factor.
Sampling Rate Conversion by Rational Factor:
In sampling rate conversion by a rational factor, interpolation is always performed to increase the sampling rate. The interpolation factor is equal to the numerator of the rational factor. For example, if the rational factor is 2/1, the interpolation factor is 2.
Decimation, on the other hand, is only performed when the rational factor is less than 1. In such cases, the decimation factor is equal to the denominator of the rational factor.
Therefore, in the given options, only interpolation (option 'A') needs to be performed in sampling rate conversion by a rational factor.
What is the partial fraction expansion of the proper function X(z)= 1/(1-1.5z-1+0.5z-2 )? - a)2z/(z-1)-z/(z+0.5)
- b)2z/(z-1)+z/(z-0.5)
- c)2z/(z-1)+z/(z+0.5)
- d)2z/(z-1)-z/(z-0.5)
Correct answer is option 'D'. Can you explain this answer?
What is the partial fraction expansion of the proper function X(z)= 1/(1-1.5z-1+0.5z-2 )?
a)
2z/(z-1)-z/(z+0.5)
b)
2z/(z-1)+z/(z-0.5)
c)
2z/(z-1)+z/(z+0.5)
d)
2z/(z-1)-z/(z-0.5)
|
|
Jyoti Sengupta answered |
Explanation: First we eliminate the negative powers of z by multiplying both numerator and denominator by z2.
Thus we obtain X(z)= z2/(z2-1.5z+0.5)
The poles of X(z) are p1=1 and p2=0.5. Consequently, the expansion will be
(X(z))/z = z/((z-1)(z-0.5)) = 2/((z-1) ) – 1/((z-0.5) )( obtained by applying partial fractions)
=>X(z)= 2z/(z-1)-z/(z-0.5).
Thus we obtain X(z)= z2/(z2-1.5z+0.5)
The poles of X(z) are p1=1 and p2=0.5. Consequently, the expansion will be
(X(z))/z = z/((z-1)(z-0.5)) = 2/((z-1) ) – 1/((z-0.5) )( obtained by applying partial fractions)
=>X(z)= 2z/(z-1)-z/(z-0.5).
Which of the following method is used to find the inverse z-transform of a signal?- a)Counter integration
- b)Expansion into a series of terms
- c)Partial fraction expansion
- d)All of the mentioned
Correct answer is option 'D'. Can you explain this answer?
Which of the following method is used to find the inverse z-transform of a signal?
a)
Counter integration
b)
Expansion into a series of terms
c)
Partial fraction expansion
d)
All of the mentioned
|
|
Nisha Das answered |
Explanation: All the methods mentioned above can be used to calculate the inverse z-transform of the given signal.
A linear time invariant system is characterized by the system function H(z)=1/(1-0.5z-1)+2/(1-3z-1 ).What is the ROC of H(z) if the system is causal? - a)|z|<3
- b)|z|>3
- c)|z|<0.5
- d)|z|>0.5
Correct answer is option 'B'. Can you explain this answer?
A linear time invariant system is characterized by the system function H(z)=1/(1-0.5z-1)+2/(1-3z-1 ).What is the ROC of H(z) if the system is causal?
a)
|z|<3
b)
|z|>3
c)
|z|<0.5
d)
|z|>0.5
|
|
Prerna Joshi answered |
Explanation: The system has poles at z=0.5 and at z=3.
Since the system is causal, its ROC is |z|>0.5 and |z|>3. The common region is |z|>3. So, ROC of given H(z) is |z|>3.
Since the system is causal, its ROC is |z|>0.5 and |z|>3. The common region is |z|>3. So, ROC of given H(z) is |z|>3.
What are the Fourier series coefficients for the signal x(n)=cosπn/3?- a)c1=c2=c3=c4=0,c1=c5=1/2
- b)c0=c1=c2=c3=c4=c5=0
- c)c0=c1=c2=c3=c4=c5=1/2
- d)None of the mentioned
Correct answer is option 'A'. Can you explain this answer?
What are the Fourier series coefficients for the signal x(n)=cosπn/3?
a)
c1=c2=c3=c4=0,c1=c5=1/2
b)
c0=c1=c2=c3=c4=c5=0
c)
c0=c1=c2=c3=c4=c5=1/2
d)
None of the mentioned
|
|
Bibek Chakraborty answered |
Explanation: In this case, f0=1/6 and hence x(n) is periodic with fundamental period N=6.
Given signal is x(n)= cosπn/3=cos2πn/6=1/2 e^(j2πn/6)+1/2 e^(-j2πn/6)
We know that -2π/6=2π-2π/6=10π/6=5(2π/6)
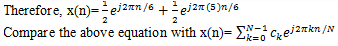
So, we get c1=c2=c3=c4=0 and c1=c5=1/2.
Given signal is x(n)= cosπn/3=cos2πn/6=1/2 e^(j2πn/6)+1/2 e^(-j2πn/6)
We know that -2π/6=2π-2π/6=10π/6=5(2π/6)
So, we get c1=c2=c3=c4=0 and c1=c5=1/2.
What is the one sided z-transform of x(n)=δ(n+k)?- a)z-k
- b)0
- c)zk
- d)1
Correct answer is option 'B'. Can you explain this answer?
What is the one sided z-transform of x(n)=δ(n+k)?
a)
z-k
b)
0
c)
zk
d)
1
|
|
Jyoti Sengupta answered |
Explanation: Since the signal x(n)= δ(n+k) is an anti causal signal i.e., it is defined for n<0 and x(n)=1 at z= -k. Since the one sided z-transform is defined only for causal signal, in this case X+(z)=0.
The Fourier series for the signal x(n)=cos√2πn exists. - a)True
- b)False
Correct answer is option 'B'. Can you explain this answer?
The Fourier series for the signal x(n)=cos√2πn exists.
a)
True
b)
False
|
|
Charvi Reddy answered |
The Fourier series for the signal x(n) = cos(n) can be found by expressing the signal as a sum of sinusoidal components with different frequencies and amplitudes.
The general form of the Fourier series representation for a periodic signal x(n) is:
x(n) = A0 + Σ[Ak * cos(kω0 * n) + Bk * sin(kω0 * n)]
where A0, Ak, and Bk are the coefficients of the Fourier series, ω0 is the fundamental frequency, and k is an integer.
For the signal x(n) = cos(n), we can see that A0 = 0, and the only non-zero coefficient is A1 = 1, since cos(n) can be written as cos(1 * n).
Therefore, the Fourier series for x(n) = cos(n) is:
x(n) = Σ[cos(ω0 * n)]
where ω0 = 1.
The general form of the Fourier series representation for a periodic signal x(n) is:
x(n) = A0 + Σ[Ak * cos(kω0 * n) + Bk * sin(kω0 * n)]
where A0, Ak, and Bk are the coefficients of the Fourier series, ω0 is the fundamental frequency, and k is an integer.
For the signal x(n) = cos(n), we can see that A0 = 0, and the only non-zero coefficient is A1 = 1, since cos(n) can be written as cos(1 * n).
Therefore, the Fourier series for x(n) = cos(n) is:
x(n) = Σ[cos(ω0 * n)]
where ω0 = 1.
What is the unit step response of the system described by the difference equation
y(n)=0.9y(n-1)-0.81y(n-2)+x(n) under the initial conditions y(-1)=y(-2)=0? - a)[1.099+1.088(0.9)n.cos(πn/3+5.2o)]u(n)
- b)[1.099+1.088(0.9)n.cos(πn/3-5.2o)]u(n)
- c)[1.099+1.088(0.9)n.cos(πn/3-5.2o)].
- d)None of the mentioned
Correct answer is option 'B'. Can you explain this answer?
What is the unit step response of the system described by the difference equation
y(n)=0.9y(n-1)-0.81y(n-2)+x(n) under the initial conditions y(-1)=y(-2)=0?
y(n)=0.9y(n-1)-0.81y(n-2)+x(n) under the initial conditions y(-1)=y(-2)=0?
a)
[1.099+1.088(0.9)n.cos(πn/3+5.2o)]u(n)
b)
[1.099+1.088(0.9)n.cos(πn/3-5.2o)]u(n)
c)
[1.099+1.088(0.9)n.cos(πn/3-5.2o)].
d)
None of the mentioned
|
|
Soumya Pillai answered |
Explanation: The system function is H(z)=1/(1-0.9z-1+0.81z-2 )
The system has two complex-conjugate poles at p1=0.9ejπ/3 and p2=0.9e -jπ/3
The z-transform of the unit step sequence is
X(z)=1/(1-z-1 )
Therefore,
Yzs(z) = 1/((1-0.9e^(jπ/3) z-1)(1-0.9e-jπ/3 z-1 )(1-z-1))
= (0.542-j0.049)/((1-0.9ejπ/3 z-1) ) + (0.542-j0.049)/((1-0.9e^(jπ/3) z-1 ) ) + 1.099/(1-z-1 )
and hence the zero state response is yzs(n)= [1.099+1.088(0.9)n.cos(πn/3-5.2o)]u(n)
Since the initial conditions are zero in this case, we can conclude that y(n)= yzs(n).
The system has two complex-conjugate poles at p1=0.9ejπ/3 and p2=0.9e -jπ/3
The z-transform of the unit step sequence is
X(z)=1/(1-z-1 )
Therefore,
Yzs(z) = 1/((1-0.9e^(jπ/3) z-1)(1-0.9e-jπ/3 z-1 )(1-z-1))
= (0.542-j0.049)/((1-0.9ejπ/3 z-1) ) + (0.542-j0.049)/((1-0.9e^(jπ/3) z-1 ) ) + 1.099/(1-z-1 )
and hence the zero state response is yzs(n)= [1.099+1.088(0.9)n.cos(πn/3-5.2o)]u(n)
Since the initial conditions are zero in this case, we can conclude that y(n)= yzs(n).
If x(n) is a stable sequence so that X(z) converges on to a unit circle, then the complex cepstrum signal is defined as:- a)X(ln X(z))
- b)ln X(z)
- c)X-1(ln X(z))
- d)None of the mentioned
Correct answer is option 'C'. Can you explain this answer?
If x(n) is a stable sequence so that X(z) converges on to a unit circle, then the complex cepstrum signal is defined as:
a)
X(ln X(z))
b)
ln X(z)
c)
X-1(ln X(z))
d)
None of the mentioned
|
|
Aarav Malik answered |
Explanation: Let us consider a sequence x(n) having a z-transform X(z). We assume that x(n) is a stable sequence so that X(z) converges on to the unit circle. The complex cepstrum of the signal x(n) is defined as the sequence cx(n), which is the inverse z-transform of Cx(z), where Cx(z)=ln X(z)
=> cx(z)= X-1(ln X(z))
=> cx(z)= X-1(ln X(z))
In general, a digital system designer has better control of tolerances in a digital signal processing system than an analog system designer who is designing an equivalent analog system. - a)True
- b)False
Correct answer is option 'A'. Can you explain this answer?
In general, a digital system designer has better control of tolerances in a digital signal processing system than an analog system designer who is designing an equivalent analog system.
a)
True
b)
False
|
|
Mrinalini Menon answered |
Explanation: Analog signal processing operations cannot be done very precisely either, since electronic components in analog systems have tolerances and they introduce noise during their operation. In general, a digital system designer has better control of tolerances in a digital signal processing system than an analog system designer who is designing an equivalent analog system.
If h(n) is the impulse response of an LTI system T and h1(n) is the impulse response of the inverse system T-1, then which of the following is true?- a)[h(n)*h1(n)].x(n)=x(n)
- b)[h(n).h1(n)].x(n)=x(n)
- c)[h(n)*h1(n)]*x(n)=x(n)
- d)[h(n).h1(n)]*x(n)=x(n)
Correct answer is option 'C'. Can you explain this answer?
If h(n) is the impulse response of an LTI system T and h1(n) is the impulse response of the inverse system T-1, then which of the following is true?
a)
[h(n)*h1(n)].x(n)=x(n)
b)
[h(n).h1(n)].x(n)=x(n)
c)
[h(n)*h1(n)]*x(n)=x(n)
d)
[h(n).h1(n)]*x(n)=x(n)
|
|
Gargi Menon answered |
Explanation: . If h(n) is the impulse response of an LTI system T and h1(n) is the impulse response of the inverse system T-1, then we know that h(n)*h1(n)=δ(n)=> [h(n)*h1(n)]*x(n)=x(n).
If the frequency response of an FIR system is given as H(z)=6+z-1-z-2, then the system is: - a)Minimum phase
- b)Maximum phase
- c)Mixed phase
- d)None of the mentioned
Correct answer is option 'A'. Can you explain this answer?
If the frequency response of an FIR system is given as H(z)=6+z-1-z-2, then the system is:
a)
Minimum phase
b)
Maximum phase
c)
Mixed phase
d)
None of the mentioned
|
|
Shubham Ghoshal answered |
Explanation: Given H(z)=6+z-1-z-2
By factoring the system function we find the zeros for the system.
The zeros of the given system are at z=-1/2,1/3
So, the system is minimum phase.
By factoring the system function we find the zeros for the system.
The zeros of the given system are at z=-1/2,1/3
So, the system is minimum phase.
If the system gives an output y(n)=H(ω)x(n) with x(n)= Aejωnas input signal, then x(n) is said to be Eigen function of the system.- a)True
- b)False
Correct answer is option 'A'. Can you explain this answer?
If the system gives an output y(n)=H(ω)x(n) with x(n)= Aejωnas input signal, then x(n) is said to be Eigen function of the system.
a)
True
b)
False
|
|
Jyoti Basak answered |
Explanation:
Definition of Eigenfunction:
An eigenfunction of a linear time-invariant system is a function that when passed through the system results in a scaled version of the original function.
Given Scenario:
In the given scenario, the system outputs y(n) = H(ω)x(n) with x(n) = Aejωn as the input signal.
Explanation of the Statement:
Since x(n) = Aejωn is the input signal and y(n) = H(ω)x(n) is the output signal, x(n) is considered an eigenfunction of the system. This is because when x(n) is processed through the system, the output is a scaled version of the original input signal.
Conclusion:
Therefore, in this case, x(n) is an eigenfunction of the system as it satisfies the definition of an eigenfunction by producing a scaled version of itself as the output signal.
Definition of Eigenfunction:
An eigenfunction of a linear time-invariant system is a function that when passed through the system results in a scaled version of the original function.
Given Scenario:
In the given scenario, the system outputs y(n) = H(ω)x(n) with x(n) = Aejωn as the input signal.
Explanation of the Statement:
Since x(n) = Aejωn is the input signal and y(n) = H(ω)x(n) is the output signal, x(n) is considered an eigenfunction of the system. This is because when x(n) is processed through the system, the output is a scaled version of the original input signal.
Conclusion:
Therefore, in this case, x(n) is an eigenfunction of the system as it satisfies the definition of an eigenfunction by producing a scaled version of itself as the output signal.
The filter with the system function H(z)=z -k is a:- a)Notch filter
- b)Band pass filter
- c)All pass filter
- d)None of the mentioned
Correct answer is option 'C'. Can you explain this answer?
The filter with the system function H(z)=z -k is a:
a)
Notch filter
b)
Band pass filter
c)
All pass filter
d)
None of the mentioned
|
|
Sakshi Tiwari answered |
Answer:
The given system function H(z) = z - k represents an all-pass filter. Let's understand why this is the correct answer.
1. All-Pass Filter:
An all-pass filter is a type of filter that allows all frequencies to pass through without attenuation but alters the phase response. In other words, the amplitude of the input signal remains unchanged, but the phase of certain frequency components is modified.
2. System Function:
The system function of a filter is a mathematical representation that relates the input signal to the output signal. It is expressed in terms of the complex variable z, which represents the unit delay operator.
In this case, the given system function H(z) = z - k represents a simple first-order difference equation. The input signal is multiplied by 'z' (unit delay), and 'k' is subtracted from it. This means that the output signal is the input signal delayed by one sample and then subtracted by a constant 'k'.
3. Frequency Response:
To analyze the frequency response of the given system function, we substitute z = e^(jω), where ω is the angular frequency.
H(z) = z - k
H(e^(jω)) = e^(jω) - k
The frequency response H(e^(jω)) can be represented as a complex number with magnitude and phase:
|H(e^(jω))| = sqrt( (Re{H(e^(jω))})^2 + (Im{H(e^(jω))})^2 )
arg{H(e^(jω))} = atan2(Im{H(e^(jω))}, Re{H(e^(jω))})
4. Magnitude and Phase Response:
For the given system function H(e^(jω)) = e^(jω) - k, the magnitude and phase responses are as follows:
|H(e^(jω))| = sqrt( (cos(ω) - k)^2 + sin^2(ω) )
arg{H(e^(jω))} = atan2(sin(ω), cos(ω) - k)
From the magnitude response, we can observe that the amplitude of the input signal remains unaffected, which is a characteristic of an all-pass filter. The phase response shows that the phase shift depends on the value of 'k'. Different values of 'k' will result in different phase shifts.
Conclusion:
Based on the analysis of the system function and frequency response, we can conclude that the given filter with the system function H(z) = z - k is an all-pass filter. It does not attenuate any frequencies but alters the phase response of the input signal.
The given system function H(z) = z - k represents an all-pass filter. Let's understand why this is the correct answer.
1. All-Pass Filter:
An all-pass filter is a type of filter that allows all frequencies to pass through without attenuation but alters the phase response. In other words, the amplitude of the input signal remains unchanged, but the phase of certain frequency components is modified.
2. System Function:
The system function of a filter is a mathematical representation that relates the input signal to the output signal. It is expressed in terms of the complex variable z, which represents the unit delay operator.
In this case, the given system function H(z) = z - k represents a simple first-order difference equation. The input signal is multiplied by 'z' (unit delay), and 'k' is subtracted from it. This means that the output signal is the input signal delayed by one sample and then subtracted by a constant 'k'.
3. Frequency Response:
To analyze the frequency response of the given system function, we substitute z = e^(jω), where ω is the angular frequency.
H(z) = z - k
H(e^(jω)) = e^(jω) - k
The frequency response H(e^(jω)) can be represented as a complex number with magnitude and phase:
|H(e^(jω))| = sqrt( (Re{H(e^(jω))})^2 + (Im{H(e^(jω))})^2 )
arg{H(e^(jω))} = atan2(Im{H(e^(jω))}, Re{H(e^(jω))})
4. Magnitude and Phase Response:
For the given system function H(e^(jω)) = e^(jω) - k, the magnitude and phase responses are as follows:
|H(e^(jω))| = sqrt( (cos(ω) - k)^2 + sin^2(ω) )
arg{H(e^(jω))} = atan2(sin(ω), cos(ω) - k)
From the magnitude response, we can observe that the amplitude of the input signal remains unaffected, which is a characteristic of an all-pass filter. The phase response shows that the phase shift depends on the value of 'k'. Different values of 'k' will result in different phase shifts.
Conclusion:
Based on the analysis of the system function and frequency response, we can conclude that the given filter with the system function H(z) = z - k is an all-pass filter. It does not attenuate any frequencies but alters the phase response of the input signal.
An IIR system with system function H(z)=(B(z))/(A(z)) is called a mixed phase if:- a)All poles and zeros are inside the unit circle
- b)All zeros are outside the unit circle
- c)All poles are outside the unit circle
- d)Some, but not all of the zeros are outside the unit circle
Correct answer is option 'D'. Can you explain this answer?
An IIR system with system function H(z)=(B(z))/(A(z)) is called a mixed phase if:
a)
All poles and zeros are inside the unit circle
b)
All zeros are outside the unit circle
c)
All poles are outside the unit circle
d)
Some, but not all of the zeros are outside the unit circle
|
|
Nitin Chawla answered |
Definition of a Mixed Phase IIR System
A mixed phase IIR (Infinite Impulse Response) system is a type of filter where some, but not all, of the zeros are located outside the unit circle in the z-plane. The system function of a mixed phase IIR system is given by:
H(z) = (B(z))/(A(z))
Where B(z) and A(z) are the numerator and denominator polynomials of the system function, respectively.
Explanation of the Correct Answer
The correct answer is option 'D': Some, but not all of the zeros are outside the unit circle. This means that in a mixed phase IIR system, there are both zeros inside and outside the unit circle.
Reasoning
To understand why option 'D' is correct, let's examine the properties of the poles and zeros in the z-plane.
Poles:
- Poles are the values of z for which the denominator polynomial A(z) becomes zero.
- Poles can be either inside or outside the unit circle.
- If all poles are inside the unit circle, the system is stable and has a causal response.
- If any poles are outside the unit circle, the system is unstable and has an anti-causal response.
Zeros:
- Zeros are the values of z for which the numerator polynomial B(z) becomes zero.
- Zeros can also be either inside or outside the unit circle.
- If all zeros are inside the unit circle, the system is causal and has a minimum phase response.
- If any zeros are outside the unit circle, the system is non-causal and has a maximum phase response.
A mixed phase IIR system:
- Combines the properties of both causal and non-causal systems.
- Has some poles inside and some poles outside the unit circle.
- Has some zeros inside and some zeros outside the unit circle.
Therefore, option 'D' is the correct answer because it accurately describes a mixed phase IIR system where some, but not all of the zeros are located outside the unit circle.
A mixed phase IIR (Infinite Impulse Response) system is a type of filter where some, but not all, of the zeros are located outside the unit circle in the z-plane. The system function of a mixed phase IIR system is given by:
H(z) = (B(z))/(A(z))
Where B(z) and A(z) are the numerator and denominator polynomials of the system function, respectively.
Explanation of the Correct Answer
The correct answer is option 'D': Some, but not all of the zeros are outside the unit circle. This means that in a mixed phase IIR system, there are both zeros inside and outside the unit circle.
Reasoning
To understand why option 'D' is correct, let's examine the properties of the poles and zeros in the z-plane.
Poles:
- Poles are the values of z for which the denominator polynomial A(z) becomes zero.
- Poles can be either inside or outside the unit circle.
- If all poles are inside the unit circle, the system is stable and has a causal response.
- If any poles are outside the unit circle, the system is unstable and has an anti-causal response.
Zeros:
- Zeros are the values of z for which the numerator polynomial B(z) becomes zero.
- Zeros can also be either inside or outside the unit circle.
- If all zeros are inside the unit circle, the system is causal and has a minimum phase response.
- If any zeros are outside the unit circle, the system is non-causal and has a maximum phase response.
A mixed phase IIR system:
- Combines the properties of both causal and non-causal systems.
- Has some poles inside and some poles outside the unit circle.
- Has some zeros inside and some zeros outside the unit circle.
Therefore, option 'D' is the correct answer because it accurately describes a mixed phase IIR system where some, but not all of the zeros are located outside the unit circle.
If x(n) is a discrete-time signal, then the value of x(n) at non integer value of ‘n’ is:- a)Zero
- b)Positive
- c)Negative
- d)Not defined
Correct answer is option 'D'. Can you explain this answer?
If x(n) is a discrete-time signal, then the value of x(n) at non integer value of ‘n’ is:
a)
Zero
b)
Positive
c)
Negative
d)
Not defined
|
|
Vaibhav Patel answered |
Explanation: For a discrete time signal, the value of x(n) exists only at integral values of n. So, for a non- integer value of ‘n’ the value of x(n) does not exist.
If the system is initially relaxed at time n=0 and memory equals to zero, then the response of such state is called as:- a)Zero-state response
- b)Zero-input response
- c)Zero-condition response
- d)None of the mentioned
Correct answer is option 'A'. Can you explain this answer?
If the system is initially relaxed at time n=0 and memory equals to zero, then the response of such state is called as:
a)
Zero-state response
b)
Zero-input response
c)
Zero-condition response
d)
None of the mentioned
|
|
Sounak Joshi answered |
Explanation: The memory of the system, describes, in some case, the ‘state’ of the system, the output of the system is called as ‘zero-state response’.
Determine the impulse response for the cascade of two LTI systems having impulse responses h1(n)=(1/2)2 u(n) and h2(n)= (1/4)2 u(n). - a)(1/2)n[2-(1/2)n], n<0
- b)(1/2)n[2-(1/2)n], n>0
- c)(1/2)n[2+(1/2)n], n<0
- d)(1/2)n[2+(1/2)n], n>0
Correct answer is option 'B'. Can you explain this answer?
Determine the impulse response for the cascade of two LTI systems having impulse responses h1(n)=(1/2)2 u(n) and h2(n)= (1/4)2 u(n).
a)
(1/2)n[2-(1/2)n], n<0
b)
(1/2)n[2-(1/2)n], n>0
c)
(1/2)n[2+(1/2)n], n<0
d)
(1/2)n[2+(1/2)n], n>0
|
|
Ishaan Saini answered |
Explanation: Let h2(n) be shifted and folded.
so, h(k)=h1(n)*h2(n)=
so, h(k)=h1(n)*h2(n)=
For k<0, h1(n)= h2(n)=0 since the unit step function is defined only on the right hand side.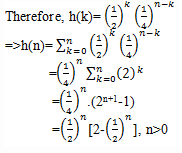
What is the condition for a signal x(n)=Brn where r=eαT to be called as an decaying exponential signal?- a)0<r<∞
- b)0<r<1
- c)r>1
- d)r<0
Correct answer is option 'B'. Can you explain this answer?
What is the condition for a signal x(n)=Brn where r=eαT to be called as an decaying exponential signal?
a)
0<r<∞
b)
0<r<1
c)
r>1
d)
r<0
|
|
Tanishq Malik answered |
Explanation: When the value of ‘r’ lies between 0 and 1 then the value of x(n) goes on decreasing exponentially with increase in value of ‘n’. So, the signal is called as decaying exponential signal.
What is the nyquist rate of the signal x(t)=3cos(50*pi*t)+10sin(300*pi*t)-cos(100*pi*t)?- a)50Hz
- b)100Hz
- c)200Hz
- d)300Hz
Correct answer is option 'D'. Can you explain this answer?
What is the nyquist rate of the signal x(t)=3cos(50*pi*t)+10sin(300*pi*t)-cos(100*pi*t)?
a)
50Hz
b)
100Hz
c)
200Hz
d)
300Hz
|
|
Hrishikesh Unni answered |
Explanation:
The frequencies present in the given signal are:
F1=25Hz
F2=150Hz
F3=50Hz
Thus,
Fmax=150Hz
and from the sampling theorem,
Nyquist rate=2*Fmax
Therefore, Fs=2*150=300Hz.
Hence, the Correct Answer is Option D
You can solve more such questions and can solve mock tests of Electrical Engineering by going through the course:
The frequencies present in the given signal are:
F1=25Hz
F2=150Hz
F3=50Hz
Thus,
Fmax=150Hz
and from the sampling theorem,
Nyquist rate=2*Fmax
Therefore, Fs=2*150=300Hz.
Hence, the Correct Answer is Option D
You can solve more such questions and can solve mock tests of Electrical Engineering by going through the course:
Time scaling operation is also known as:- a)Down-sampling
- b)Up-sampling
- c)Sampling
- d)None of the mentioned
Correct answer is option 'A'. Can you explain this answer?
Time scaling operation is also known as:
a)
Down-sampling
b)
Up-sampling
c)
Sampling
d)
None of the mentioned
|
|
Amrutha Singh answered |
Explanation: If the signal x(n) was originally obtained by sampling a signal xa(t), then x(n)=xa(nT). Now, y(n)=x(2n)(say)=xa(2nT). Hence the time scaling operation is equivalent to changing the sampling rate from 1/T to 1/2T, that is to decrease the rate by a factor of 2. So, time scaling is also called as down-sampling.
The difference between the unquantized x(n) and quantized xq(n) is known as:- a)Quantization coefficient
- b)Quantization ratio
- c)Quantization factor
- d)Quantization error
Correct answer is option 'D'. Can you explain this answer?
The difference between the unquantized x(n) and quantized xq(n) is known as:
a)
Quantization coefficient
b)
Quantization ratio
c)
Quantization factor
d)
Quantization error
|
|
Suyash Chauhan answered |
Explanation: Quantization error is the difference in the signal obtained after sampling i.e., x(n) and the signal obtained after quantization i.e., xq(n) at any instant of time.
The system described by the input-output equation y(n)=nx(n)+bx3(n) is a: - a)Static system
- b)Dynamic system
- c)Identical system
- d)None of the mentioned
Correct answer is option 'A'. Can you explain this answer?
The system described by the input-output equation y(n)=nx(n)+bx3(n) is a:
a)
Static system
b)
Dynamic system
c)
Identical system
d)
None of the mentioned
|
|
Ameya Goyal answered |
Explanation: Since the output of the system y(n) depends only on the present value of the input x(n) but not on the past or the future values of the input, the system is called as static or memory-less system.
What is the cross correlation sequence of the following sequences?
x(n)={….0,0,2,-1,3,7,1,2,-3,0,0….}
y(n)={….0,0,1,-1,2,-2,4,1,-2,5,0,0….}- a){10,9,19,36,-14,33,0,7,13,-18,16,7,5,-3}
- b){10,-9,19,36,-14,33,0,7,13,-18,16,-7,5,-3}
- c){10,9,19,36,14,33,0,-7,13,-18,16,-7,5,-3}
- d){10,-9,19,36,-14,33,0,-7,13,18,16,7,5,-3}
Correct answer is option 'B'. Can you explain this answer?
What is the cross correlation sequence of the following sequences?
x(n)={….0,0,2,-1,3,7,1,2,-3,0,0….}
y(n)={….0,0,1,-1,2,-2,4,1,-2,5,0,0….}
x(n)={….0,0,2,-1,3,7,1,2,-3,0,0….}
y(n)={….0,0,1,-1,2,-2,4,1,-2,5,0,0….}
a)
{10,9,19,36,-14,33,0,7,13,-18,16,7,5,-3}
b)
{10,-9,19,36,-14,33,0,7,13,-18,16,-7,5,-3}
c)
{10,9,19,36,14,33,0,-7,13,-18,16,-7,5,-3}
d)
{10,-9,19,36,-14,33,0,-7,13,18,16,7,5,-3}
|
|
Shubham Das answered |
Explanation:
Which of the following is the auto correlation of x(n)? - a)rxy(l)=x(l)*x(-l)
- b)rxy(l)=x(l)*x(l)
- c)rxy(l)=x(l)+x(-l)
- d)None of the mentioned
Correct answer is option 'A'. Can you explain this answer?
Which of the following is the auto correlation of x(n)?
a)
rxy(l)=x(l)*x(-l)
b)
rxy(l)=x(l)*x(l)
c)
rxy(l)=x(l)+x(-l)
d)
None of the mentioned
|
|
Vaibhav Banerjee answered |
Explanation: We know that, the correlation of two signals x(n) and y(n) is
If ‘F’ is the frequency of the analog signal, then what is the minimum sampling rate required to avoid aliasing?- a)F
- b)2F
- c)3F
- d)4F
Correct answer is option 'A'. Can you explain this answer?
If ‘F’ is the frequency of the analog signal, then what is the minimum sampling rate required to avoid aliasing?
a)
F
b)
2F
c)
3F
d)
4F
|
|
Atharva Das answered |
Explanation: According to Nyquist rate, to avoid aliasing the sampling frequency should be equal to twice of the analog frequency.
What is the ROC of z-transform of finite duration anti-causal sequence?- a)z=0
- b)z=∞
- c)Entire z-plane, except at z=0
- d)Entire z-plane, except at z=∞
Correct answer is option 'D'. Can you explain this answer?
What is the ROC of z-transform of finite duration anti-causal sequence?
a)
z=0
b)
z=∞
c)
Entire z-plane, except at z=0
d)
Entire z-plane, except at z=∞
|
|
Rahul Chavan answered |
Explanation: Let us an example of anti causal sequence whose z-transform will be in the form X(z)=1+z+z2 which has a finite value at all values of ‘z’ except at z=∞.So, ROC of an anti-causal sequence is entire z-plane except at z=∞.
For a continuous time signal x(t) to be periodic with a period T, then x(t+mT) should be equal to:- a)x(-t)
- b)x(mT)
- c)x(mt)
- d)x(t)
Correct answer is option 'D'. Can you explain this answer?
For a continuous time signal x(t) to be periodic with a period T, then x(t+mT) should be equal to:
a)
x(-t)
b)
x(mT)
c)
x(mt)
d)
x(t)
|
|
Yashvi Das answered |
Explanation: If a signal x(t) is said to be periodic with period T, then x(t+mT)=x(t) for all t and any integer m.
What is the ROC of the system function H(z) if the discrete time LTI system is BIBO stable?- a)Entire z-plane, except at z=0
- b)Entire z-plane, except at z=∞
- c)Contain unit circle
- d)None of the mentioned
Correct answer is option 'C'. Can you explain this answer?
What is the ROC of the system function H(z) if the discrete time LTI system is BIBO stable?
a)
Entire z-plane, except at z=0
b)
Entire z-plane, except at z=∞
c)
Contain unit circle
d)
None of the mentioned
|
|
Rahul Chavan answered |
Explanation: A discrete time LTI is BIBO stable, if and only if its impulse response h(n) is absolutely summable. That is,
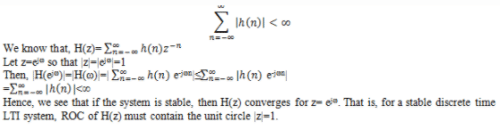
What is the period of cos2t+sin3t?- a)pi
- b)2*pi
- c)3*pi
- d)4*pi
Correct answer is option 'B'. Can you explain this answer?
What is the period of cos2t+sin3t?
a)
pi
b)
2*pi
c)
3*pi
d)
4*pi
|
|
Pritam Chatterjee answered |
Explanation: Period of cos2t=(2*pi)/2=pi
Period of sin3t=(2*pi)/3
LCM of pi and (2*pi)/3 is 2*pi.
Period of sin3t=(2*pi)/3
LCM of pi and (2*pi)/3 is 2*pi.
Chapter doubts & questions for Introduction to Digital Signal Processing - Digital Signal Processing 2025 is part of Electronics and Communication Engineering (ECE) exam preparation. The chapters have been prepared according to the Electronics and Communication Engineering (ECE) exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Electronics and Communication Engineering (ECE) 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Introduction to Digital Signal Processing - Digital Signal Processing in English & Hindi are available as part of Electronics and Communication Engineering (ECE) exam.
Download more important topics, notes, lectures and mock test series for Electronics and Communication Engineering (ECE) Exam by signing up for free.
Digital Signal Processing
3 videos|75 docs|54 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup











