All Exams >
SSC CGL >
Statistics for SSC CGL (Hindi) >
All Questions
All questions of केंद्रीय प्रवृत्ति के उपाय for SSC CGL Exam
दिए गए संख्याओं के सेट 2, 6, 6, 8, 4, 2, 7, 9 का माध्यिका ज्ञात करें।- a)6
- b)8
- c)4
- d)5
- e)उपरोक्त में से कोई नहीं
Correct answer is option 'A'. Can you explain this answer?
दिए गए संख्याओं के सेट 2, 6, 6, 8, 4, 2, 7, 9 का माध्यिका ज्ञात करें।
a)
6
b)
8
c)
4
d)
5
e)
उपरोक्त में से कोई नहीं
|
EduRev SSC CGL answered |
संкон्सेप्ट:
माध्य: माध्य (Median) एक क्रमबद्ध (Ascending या Descending) संख्या की सूची में मध्य संख्या होती है।
मामला 1: यदि अवलोकनों (n) की संख्या सम (Even) है
मामला 2: यदि अवलोकनों (n) की संख्या विषम (Odd) है
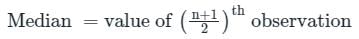
गणना:
मामला 2: यदि अवलोकनों (n) की संख्या विषम (Odd) है
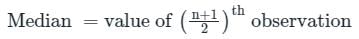
गणना:
दिए गए मान 2, 6, 6, 8, 4, 2, 7, 9
अवलोकनों को बढ़ते क्रम में व्यवस्थित करें:
2, 2, 4, 6, 6, 7, 8, 9
यहाँ, n = 8 = सम
जैसा कि हम जानते हैं, यदि n सम है तो,
माध्य और माध्यिका के मान क्रमशः 22.5 और 20 दिए गए हैं। मोड का अनुमानित मान खोजें।- a)15
- b)20
- c)12
- d)13.5
- e)none of the above
Correct answer is option 'A'. Can you explain this answer?
माध्य और माध्यिका के मान क्रमशः 22.5 और 20 दिए गए हैं। मोड का अनुमानित मान खोजें।
a)
15
b)
20
c)
12
d)
13.5
e)
none of the above
|
Ssc Cgl answered |
व्यावहारिक माध्य माध्यिका मोड संबंध इस प्रकार दिया गया है:
माध्य - मोड = 3(माध्य - माध्यिका)
दिया गया माध्य = 22.5 और माध्यिका = 20
22.5 - मोड = 3(22.5 - 20)
मोड = 15
माध्य - मोड = 3(माध्य - माध्यिका)
दिया गया माध्य = 22.5 और माध्यिका = 20
22.5 - मोड = 3(22.5 - 20)
मोड = 15
4.1, 5.2, 6.3, 3.6, 2.4, 6.4, 4.6 की माध्यिका ज्ञात करें।- a)5.2
- b)4.6
- c)4.1
- d)2.4
- e)उपरोक्त में से कोई नहीं
Correct answer is option 'B'. Can you explain this answer?
4.1, 5.2, 6.3, 3.6, 2.4, 6.4, 4.6 की माध्यिका ज्ञात करें।
a)
5.2
b)
4.6
c)
4.1
d)
2.4
e)
उपरोक्त में से कोई नहीं
|
|
EduRev SSC CGL answered |
संकल्पना:
माध्यिका: यह दिए गए सेट में मध्य मान होता है, जबकि सेट को या तो बढ़ते या घटते क्रम में व्यवस्थित किया जाता है।
यदि अवलोकनों की संख्या (n) विषम है तो माध्यिका (n+1)/2वां पद होता है।
यदि अवलोकनों की संख्या (n) सम है तो माध्यिका n वें और (n+1) वें पद का औसत होता है।
गणना:
दिए गए डेटा हैं 4.1, 5.2, 6.3, 3.6, 2.4, 6.4, 4.6
दिए गए डेटा का बढ़ता क्रम: 2.4, 3.6, 4.1, 4.6, 5.2, 6.3, 6.4
अवलोकनों की संख्या विषम है (n = 7)
इसलिए, माध्यिका (n+1)/2वां पद या 4वां पद है
माध्यिका 4वें पद यानी 4.6 है।
4.1, 5.2, 6.3, 3.6, 2.4, 6.4, 4.6 का मध्य मान खोजें।- a)5.2
- b)6.4
- c)4.1
- d)2.4
- e)उपर्युक्त में से कोई नहीं
Correct answer is option 'E'. Can you explain this answer?
4.1, 5.2, 6.3, 3.6, 2.4, 6.4, 4.6 का मध्य मान खोजें।
a)
5.2
b)
6.4
c)
4.1
d)
2.4
e)
उपर्युक्त में से कोई नहीं
|
|
EduRev SSC CGL answered |
धारणा:
माध्यिका: यह दिए गए सेट में मध्य मान है, जबकि सेट या तो बढ़ते या घटते क्रम में हो सकता है।
माध्यिका: यह दिए गए सेट में मध्य मान है, जबकि सेट या तो बढ़ते या घटते क्रम में हो सकता है।
यदि अवलोकनों की संख्या (n) विषम है, तो माध्यिका (n+1)/2वां पद होगा।
यदि अवलोकनों की संख्या (n) सम है, तो माध्यिका nवें और (n+1)वें पद का औसत होगा।
गणना:
गणना:
दिए गए डेटा हैं 4.1, 5.2, 6.3, 3.6, 2.4, 6.4, 4.6
दिए गए डेटा का बढ़ता क्रम: 2.4, 3.6, 4.1, 4.6, 5.2, 6.3, 6.4
अवलोकनों की संख्या विषम है (n = 7)
इसलिए, माध्यिका (n+1)/2वां पद या 4वां पद है।
माध्यिका 4वां पद है अर्थात्, 4.6
संख्याओं 10, 8, 2, 7, 3, 8, 5, 1 का माध्यिका k है। यदि 10 को 1 से बदल दिया जाए, तो नई माध्यिका r है। (k - r) का मान क्या है?- a)-1.5
- b)0
- c)1
- d)उपरोक्त में से एक से अधिक
- e)उपरोक्त में से कोई नहीं
Correct answer is option 'E'. Can you explain this answer?
संख्याओं 10, 8, 2, 7, 3, 8, 5, 1 का माध्यिका k है। यदि 10 को 1 से बदल दिया जाए, तो नई माध्यिका r है। (k - r) का मान क्या है?
a)
-1.5
b)
0
c)
1
d)
उपरोक्त में से एक से अधिक
e)
उपरोक्त में से कोई नहीं
|
|
EduRev SSC CGL answered |
दी गई जानकारी:
संख्याएँ: 10, 8, 2, 7, 3, 8, 5, 1
संख्याओं के समूह की माध्यिका खोजने के लिए, हम संख्याओं को आरोही क्रम में व्यवस्थित करते हैं और मध्य मान निकालते हैं। यदि मानों की कुल संख्या विषम है, तो माध्यिका मध्य मान होता है। यदि मानों की कुल संख्या सम है, तो माध्यिका दो मध्य मानों का औसत होता है।
गणना:
संख्याओं को आरोही क्रम में व्यवस्थित करते हैं:
⇒ 1, 2, 3, 5, 7, 8, 8, 10
माध्यिका (k) निकालना: चूंकि मानों की कुल संख्या 8 है, माध्यिका दो मध्य मानों का औसत है:
⇒ (5 + 7) / 2 = 6।
10 को 1 से बदलने के बाद नए संख्याओं के सेट को आरोही क्रम में व्यवस्थित करते हैं:
⇒ 1, 1, 2, 3, 5, 7, 8, 8
नई माध्यिका (r) निकालना: चूंकि मानों की कुल संख्या अभी भी 8 है, माध्यिका दो मध्य मानों का औसत है:
⇒ (3 + 5) / 2 = 4।
(k - r) की गणना करते हैं
⇒ 6 - 4 = 2।
इसलिए, (k - r) का मान 2 है।
n अवलोकनों का एक डेटा सेट का औसत 2M है, जबकि 2n अवलोकनों का दूसरा डेटा सेट का औसत M है। संयुक्त डेटा सेट का औसत क्या होगा?- a)एम
- b)3M/2
- c)2M/3
- d)4M/3
- e)उपरोक्त में से कोई नहीं
Correct answer is option 'D'. Can you explain this answer?
n अवलोकनों का एक डेटा सेट का औसत 2M है, जबकि 2n अवलोकनों का दूसरा डेटा सेट का औसत M है। संयुक्त डेटा सेट का औसत क्या होगा?
a)
एम
b)
3M/2
c)
2M/3
d)
4M/3
e)
उपरोक्त में से कोई नहीं
|
|
EduRev SSC CGL answered |
संकल्पना:
संयुक्त औसत:
मान लें कि x1 और x2 पहले और दूसरे समूह के डेटा के औसत हैं, जिनमें क्रमशः n1 और n2 आइटम हैं।
तो संयुक्त औसत होगा:
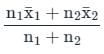
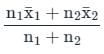
गणना:
दी गई जानकारी:
n1 = n और x1 = 2M
n2 = 2n और x2 = M
संयुक्त औसत होगा:
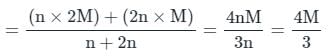
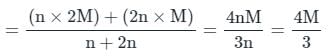
डेटा सेट में मोड क्या है?- a)डेटा सेट में सबसे छोटा संख्या
- b)वह संख्या जो कम बार होती है
- c)वह संख्या जो सबसे अधिक बार होती है
- d)डेटा सेट में सबसे बड़ा संख्या
- e)None of the above
Correct answer is option 'C'. Can you explain this answer?
डेटा सेट में मोड क्या है?
a)
डेटा सेट में सबसे छोटा संख्या
b)
वह संख्या जो कम बार होती है
c)
वह संख्या जो सबसे अधिक बार होती है
d)
डेटा सेट में सबसे बड़ा संख्या
e)
None of the above
|
|
EduRev SSC CGL answered |
डेटा सेट में सबसे अधिक बार आने वाली संख्या को मोड कहा जाता है। एक संख्या का समूह एक से अधिक मोड भी रख सकता है।
संचयी आवृत्ति तालिका का निर्माण किसके निर्धारण में सहायक होता है?- a)मोड
- b)माध्यिका
- c)सामान्य
- d)उपरोक्त तीनों उपाय
- e)None of the above
Correct answer is option 'B'. Can you explain this answer?
संचयी आवृत्ति तालिका का निर्माण किसके निर्धारण में सहायक होता है?
a)
मोड
b)
माध्यिका
c)
सामान्य
d)
उपरोक्त तीनों उपाय
e)
None of the above
|
|
Ssc Cgl answered |
माध्यिका
संविधानात्मक आवृत्ति वितरण में, आवृत्ति का योग उस वर्ग की आवृत्ति और उसके नीचे सभी वर्गों की आवृत्ति होता है।
इसका अर्थ है कि हम एक मान और उसके पहले आए सभी मानों को जोड़कर संविधानात्मक आवृत्ति प्राप्त कर सकते हैं।
इसके अलावा,
किसी भी वर्ग की आवृत्ति = वर्ग की संविधानात्मक आवृत्ति - पूर्ववर्ती वर्ग की संविधानात्मक आवृत्ति।
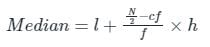
l = माध्यिका वर्ग अंतराल की निचली सीमा
cf = माध्यिका वर्ग आवृत्ति से पूर्ववर्ती संविधानात्मक आवृत्ति
f = वर्ग अंतराल की आवृत्ति जिसमें माध्यिका है
h = वर्ग अंतराल की चौड़ाई
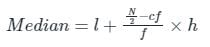
l = माध्यिका वर्ग अंतराल की निचली सीमा
cf = माध्यिका वर्ग आवृत्ति से पूर्ववर्ती संविधानात्मक आवृत्ति
f = वर्ग अंतराल की आवृत्ति जिसमें माध्यिका है
h = वर्ग अंतराल की चौड़ाई
दी गई डेटा का माध्य खोजें:
- a)39.95
- b)35.70
- c)43.95
- d)23.95
- e)उपर्युक्त में से कोई नहीं
Correct answer is option 'B'. Can you explain this answer?
दी गई डेटा का माध्य खोजें:
a)
39.95
b)
35.70
c)
43.95
d)
23.95
e)
उपर्युक्त में से कोई नहीं
|
|
Ssc Cgl answered |
समूहित डेटा का माध्य इस प्रकार दिया जाता है,
दी गई जानकारी:
दी गई जानकारी:
गणना:
अब, डेटा का माध्य निकालने के लिए हमें ∑fiXi और ∑fi निम्नलिखित के अनुसार निकालना होगा,
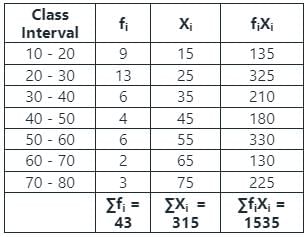
फिर,
हमें पता है कि, समूहित डेटा का माध्य इस प्रकार दिया जाता है
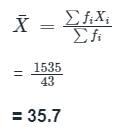
इसलिए, समूहित डेटा का माध्य 35.7 है।
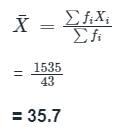
इसलिए, समूहित डेटा का माध्य 35.7 है।
डेटा का मोड खोजें: 13, 16, 12, 14, 19, 12, 14, 13, 14- a)13
- b)19
- c)14
- d)कोई मोड नहीं
- e)none of the above
Correct answer is option 'C'. Can you explain this answer?
डेटा का मोड खोजें: 13, 16, 12, 14, 19, 12, 14, 13, 14
a)
13
b)
19
c)
14
d)
कोई मोड नहीं
e)
none of the above
|
|
Ssc Cgl answered |
दी गई डेटा = 13, 16, 12, 14, 19, 12, 14, 13, 14
डेटा को बढ़ते क्रम में व्यवस्थित करने पर हमें मिलता है
12, 12, 13, 13, 14, 14, 14, 16, 19।
मोड वह अवलोकन है जो सबसे अधिक बार होता है।
14 दिए गए डेटा में तीन बार आता है।
अतः मोड = 14
दिए गए नमूनों का मोड खोजें।
47, 25, 15, 89, 47, 89, 89, 1, 47, 73, 29, 64, 95, 90, 47, 25।- a)85
- b)47
- c)25
- d)कोई मोड नहीं
- e)none of the above
Correct answer is option 'B'. Can you explain this answer?
दिए गए नमूनों का मोड खोजें।
47, 25, 15, 89, 47, 89, 89, 1, 47, 73, 29, 64, 95, 90, 47, 25।
47, 25, 15, 89, 47, 89, 89, 1, 47, 73, 29, 64, 95, 90, 47, 25।
a)
85
b)
47
c)
25
d)
कोई मोड नहीं
e)
none of the above
|
|
Ssc Cgl answered |
89 और 25 दो बार आते हैं, 64 एक बार आता है, 47 चार बार आता है।
चूंकि 47 उपरोक्त डेटा सेट में चार बार आया है और अन्य संख्या उससे कम हैं। उपरोक्त डेटा सेट का मोड 47 है।
चूंकि 47 उपरोक्त डेटा सेट में चार बार आया है और अन्य संख्या उससे कम हैं। उपरोक्त डेटा सेट का मोड 47 है।
नीचे छात्रों के एक परीक्षा के परिणाम दिए गए हैं। दिए गए परिणामों का मोड खोजें।
90, 80, 77, 86, 90, 91, 77, 25, 45, 35, 66, 69, 65, 43, 65, 75, 43, 90, 89।- a)43
- b)77
- c)65
- d)90
- e)उपरोक्त में से कोई नहीं
Correct answer is option 'D'. Can you explain this answer?
नीचे छात्रों के एक परीक्षा के परिणाम दिए गए हैं। दिए गए परिणामों का मोड खोजें।
90, 80, 77, 86, 90, 91, 77, 25, 45, 35, 66, 69, 65, 43, 65, 75, 43, 90, 89।
90, 80, 77, 86, 90, 91, 77, 25, 45, 35, 66, 69, 65, 43, 65, 75, 43, 90, 89।
a)
43
b)
77
c)
65
d)
90
e)
उपरोक्त में से कोई नहीं
|
|
EduRev SSC CGL answered |
90 तीन बार आया। 77, 43 और 65 दो बार आए।
उपरोक्त डेटा सेट में, 90 तीन बार आया और अन्य संख्याएँ एक या दो बार आईं। इसलिए, 90 उपरोक्त डेटा सेट का मोड है।
उपरोक्त डेटा सेट में, 90 तीन बार आया और अन्य संख्याएँ एक या दो बार आईं। इसलिए, 90 उपरोक्त डेटा सेट का मोड है।
मान लें कि x, y, z तीन अवलोकन हैं। इन अवलोकनों का माध्य है- a)
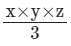
- b)
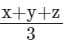
- c)
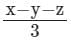
- d)
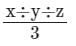
- e)None of the above
Correct answer is option 'B'. Can you explain this answer?
मान लें कि x, y, z तीन अवलोकन हैं। इन अवलोकनों का माध्य है
a)
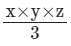
b)
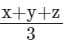
c)
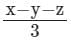
d)
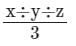
e)
None of the above
|
|
EduRev SSC CGL answered |
दी गई जानकारी:
तीन अवलोकन = x, y, z
उपयोग की गई अवधारणा:
किसी अवलोकनों के सेट का माध्य (औसत) सभी अवलोकनों को जोड़कर और फिर अवलोकनों की संख्या से विभाजित करके निकाला जाता है।
गणना:
इन अवलोकनों (x, y, z) का माध्य (M) निम्नलिखित द्वारा दिया गया है:
⇒ माध्य = (x + y + z) / 3
∴ तीन अवलोकनों का माध्य (x + y + z) / 3 है।
यदि 14, 13, 18, 16, k, (k + 3) का औसत 13 है, तो k, 8, 9, 11, 5, 10, 6 का औसत क्या होगा?- a)7
- b)8
- c)9
- d)उपरोक्त में से एक से अधिक
- e)उपरोक्त में से कोई नहीं
Correct answer is option 'B'. Can you explain this answer?
यदि 14, 13, 18, 16, k, (k + 3) का औसत 13 है, तो k, 8, 9, 11, 5, 10, 6 का औसत क्या होगा?
a)
7
b)
8
c)
9
d)
उपरोक्त में से एक से अधिक
e)
उपरोक्त में से कोई नहीं
|
|
Ssc Cgl answered |
14, 13, 18, 16, k, (k + 3) का औसत 13 है, जिसका मतलब है
⇒ [14 + 13 + 18 + 16 + k + (k + 3)]/6 = 13
⇒ [ 2k + 64] = 78
⇒ k = 7
फिर, k, 8, 9, 11, 5, 10, 6 का औसत है
⇒ [k + 8 + 9 + 11 + 5 + 10 + 6]/7
⇒ [7 + 8 + 9 + 11 + 5 + 10 + 6]/7
⇒ 56/7
⇒ 8
∴ सही उत्तर 8 है
यदि कुछ डेटा का सामान्य (mean) और मोड (mode) क्रमशः 4 और 10 हैं, तो इसका माध्यिका (median) क्या होगा?- a)1.5
- b)5.3
- c)16
- d)6
- e)उपरोक्त में से कोई नहीं
Correct answer is option 'D'. Can you explain this answer?
यदि कुछ डेटा का सामान्य (mean) और मोड (mode) क्रमशः 4 और 10 हैं, तो इसका माध्यिका (median) क्या होगा?
a)
1.5
b)
5.3
c)
16
d)
6
e)
उपरोक्त में से कोई नहीं
|
|
EduRev SSC CGL answered |
दी गई जानकारी के अनुसार,
डेटा का सामान्य (mean) = 4 और मोड (mode) = 10 है।
हमें पता है कि
मोड = 3(माध्यिका) - 2(सामान्य)
⇒ 10 = 3(माध्यिका) - 2(4)
⇒ 3(माध्यिका) = 18
⇒ माध्यिका = 6
इसलिए, डेटा का माध्यिका 6 होगा।
यदि 10 संख्याओं का औसत 96 है और इनमें से एक संख्या 150 है, तो शेष नौ संख्याओं का औसत क्या होगा?- a)60
- b)75
- c)81
- d)उपरोक्त में से एक से अधिक
- e)उपरोक्त में से कोई नहीं
Correct answer is option 'E'. Can you explain this answer?
यदि 10 संख्याओं का औसत 96 है और इनमें से एक संख्या 150 है, तो शेष नौ संख्याओं का औसत क्या होगा?
a)
60
b)
75
c)
81
d)
उपरोक्त में से एक से अधिक
e)
उपरोक्त में से कोई नहीं
|
|
EduRev SSC CGL answered |
यहाँ, 10 संख्याओं का औसत 96 है,
तो, 10 संख्याओं का कुल = 96 × 10 = 960
यदि एक संख्या 150 है, तो शेष 9 संख्याओं का कुल = (960 - 150) = 810
अब, शेष नौ संख्याओं का औसत = 810/9 = 90
इसलिए, सही उत्तर है 90
8, 5, 7, 10, 15, 21, 5, 7, 2, 5 का मोड क्या है?- a)2
- b)5
- c)7
- d)21
- e)उपरोक्त में से कोई नहीं
Correct answer is option 'B'. Can you explain this answer?
8, 5, 7, 10, 15, 21, 5, 7, 2, 5 का मोड क्या है?
a)
2
b)
5
c)
7
d)
21
e)
उपरोक्त में से कोई नहीं
|
|
Ssc Cgl answered |
डेटा सेट में मोड को उस संख्या के रूप में परिभाषित किया जाता है जो डेटा सेट में सबसे अधिक बार होती है।
5 तीन बार, 7 दो बार, 2 और 21 एक बार प्रत्येक हुई।
5, परिभाषा के अनुसार, सबसे अधिक पुनरावृत्त संख्या है।
5 तीन बार, 7 दो बार, 2 और 21 एक बार प्रत्येक हुई।
5, परिभाषा के अनुसार, सबसे अधिक पुनरावृत्त संख्या है।
19, 18, 9, 24, 1, 12, 23, 75 का मोड क्या है?- a)75
- b)1
- c)19
- d)कोई मोड नहीं
- e)उपरोक्त में से कोई नहीं
Correct answer is option 'D'. Can you explain this answer?
19, 18, 9, 24, 1, 12, 23, 75 का मोड क्या है?
a)
75
b)
1
c)
19
d)
कोई मोड नहीं
e)
उपरोक्त में से कोई नहीं
|
|
EduRev SSC CGL answered |
मोड की परिभाषा के अनुसार, मोड वह संख्या होती है जो सबसे अधिक बार होती है। ऐसी कोई संख्या नहीं है जो एक से अधिक बार दोहराई गई हो। इसलिए, हम कह सकते हैं कि कोई मोड नहीं है।
निम्नलिखित वितरण में, माध्यिका का मान 46 है, और x + y = 78, तब x और y के मान हैं: 
- a)40,39
- b)42,37
- c)33,45
- d)38,41
- e)उपरोक्त में से कोई नहीं
Correct answer is option 'C'. Can you explain this answer?
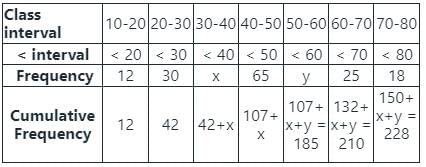
निम्नलिखित वितरण में, माध्यिका का मान 46 है, और x + y = 78, तब x और y के मान हैं:
a)
40,39
b)
42,37
c)
33,45
d)
38,41
e)
उपरोक्त में से कोई नहीं
|
|
EduRev SSC CGL answered |
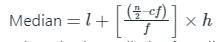
जहां l = मध्य वर्ग की निम्न सीमा,
n = अवलोकनों की संख्या,
h = वर्ग का आकार, f = मध्य वर्ग की आवृत्ति,
cf = मध्य वर्ग के पूर्ववर्ती वर्ग की संचयी आवृत्ति।
गणना:
गणना:
दी गई तालिका से हमने मध्य को खोजने के लिए उपरोक्त संचयी आवृत्ति की तालिका बनाई है।
तालिका में, n = 150 + x + y = 150 + 78 = 228
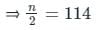
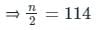
जो 42 + x और 107 + x के बीच होगा,
इसलिए, मध्य वर्ग: 40 - 50
l = 40, f = 65, cf = 42+x
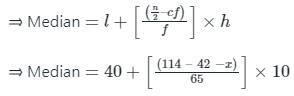
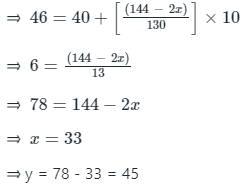
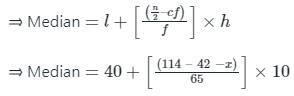
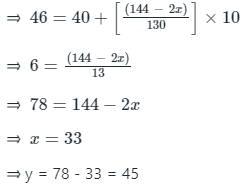
दी गई डेटा का औसत खोजें:
- a)30.95
- b)35.70
- c)43.95
- d)23.95
- e)none of the above
Correct answer is option 'B'. Can you explain this answer?
दी गई डेटा का औसत खोजें:
a)
30.95
b)
35.70
c)
43.95
d)
23.95
e)
none of the above
|
|
Ssc Cgl answered |
प्रयुक्त सूत्र:
समूहित डेटा का औसत दिया गया है,
दिया गया
दिया गया
गणना:
अब, डेटा का औसत निकालने के लिए ∑fiXi और ∑fi नीचे दिए गए अनुसार खोजने होंगे,
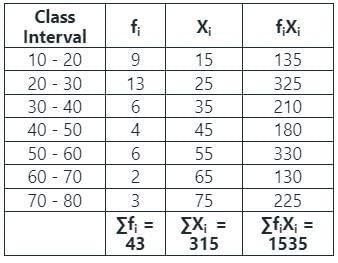
फिर,
हमें पता है कि, समूहित डेटा का औसत दिया गया है
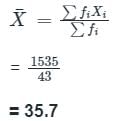
इसलिए, समूहित डेटा का औसत 35.7 है।
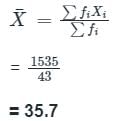
इसलिए, समूहित डेटा का औसत 35.7 है।
Chapter doubts & questions for केंद्रीय प्रवृत्ति के उपाय - Statistics for SSC CGL (Hindi) 2025 is part of SSC CGL exam preparation. The chapters have been prepared according to the SSC CGL exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for SSC CGL 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of केंद्रीय प्रवृत्ति के उपाय - Statistics for SSC CGL (Hindi) in English & Hindi are available as part of SSC CGL exam.
Download more important topics, notes, lectures and mock test series for SSC CGL Exam by signing up for free.
Statistics for SSC CGL (Hindi)
39 videos|66 docs|18 tests
|
Signup to see your scores go up within 7 days!
Study with 1000+ FREE Docs, Videos & Tests
10M+ students study on EduRev
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup