All Exams >
SSC CGL >
SSC CGL Tier 2 - Study Material, Online Tests, Previous Year (Hindi) >
All Questions
All questions of एचसीएफ और एलसीएम (HCF & LCM) for SSC CGL Exam
दो संख्याओं का गुणनफल 2160 है और उनका HCF 12 है। ऐसी संभावित जोड़ों की संख्या क्या है?- a)2
- b)1
- c)4
- d)3
Correct answer is option 'A'. Can you explain this answer?
दो संख्याओं का गुणनफल 2160 है और उनका HCF 12 है। ऐसी संभावित जोड़ों की संख्या क्या है?
a)
2
b)
1
c)
4
d)
3

|
Mainak Verma answered |
समस्या का विश्लेषण
दिए गए हैं:
- गुणनफल (Product) = 2160
- HCF (Highest Common Factor) = 12
संख्याएँ और उनके गुणनफल
जब दो संख्याएँ A और B हैं, तो:
A * B = 2160
और HCF(A, B) = 12
संख्याओं का निर्माण
हम जानते हैं कि यदि HCF 12 है, तो हम इन संख्याओं को इस प्रकार लिख सकते हैं:
A = 12m और B = 12n, जहाँ m और n पूर्णांक हैं।
अब, गुणनफल को देखते हैं:
12m * 12n = 2160
इससे हमें मिलता है:
144mn = 2160
इसका समाधान करते हैं:
mn = 15
mn = 15 के संयोजन
अब, हमें m और n के सभी संभावित संयोजन खोजने हैं जो mn = 15 को संतुष्ट करते हैं। 15 के गुणनखंड हैं:
- (1, 15)
- (3, 5)
- (5, 3)
- (15, 1)
संख्याओं की जोड़ी
इन संयोजनों से हमें चार संभावित जोड़े मिलते हैं:
- (12 * 1, 12 * 15) = (12, 180)
- (12 * 3, 12 * 5) = (36, 60)
- (12 * 5, 12 * 3) = (60, 36)
- (12 * 15, 12 * 1) = (180, 12)
संख्याओं की अदला-बदली
ध्यान दें कि (A, B) और (B, A) एक ही जोड़ी के रूप में गिनी जाती हैं। इसलिए, हमें केवल अद्वितीय जोड़े गिनने हैं।
अंतिम उत्तर
इस प्रकार, संभावित अद्वितीय जोड़ों की संख्या 2 है:
- (12, 180) और (36, 60)
इसलिए, सही उत्तर विकल्प 'A' है।
दिए गए हैं:
- गुणनफल (Product) = 2160
- HCF (Highest Common Factor) = 12
संख्याएँ और उनके गुणनफल
जब दो संख्याएँ A और B हैं, तो:
A * B = 2160
और HCF(A, B) = 12
संख्याओं का निर्माण
हम जानते हैं कि यदि HCF 12 है, तो हम इन संख्याओं को इस प्रकार लिख सकते हैं:
A = 12m और B = 12n, जहाँ m और n पूर्णांक हैं।
अब, गुणनफल को देखते हैं:
12m * 12n = 2160
इससे हमें मिलता है:
144mn = 2160
इसका समाधान करते हैं:
mn = 15
mn = 15 के संयोजन
अब, हमें m और n के सभी संभावित संयोजन खोजने हैं जो mn = 15 को संतुष्ट करते हैं। 15 के गुणनखंड हैं:
- (1, 15)
- (3, 5)
- (5, 3)
- (15, 1)
संख्याओं की जोड़ी
इन संयोजनों से हमें चार संभावित जोड़े मिलते हैं:
- (12 * 1, 12 * 15) = (12, 180)
- (12 * 3, 12 * 5) = (36, 60)
- (12 * 5, 12 * 3) = (60, 36)
- (12 * 15, 12 * 1) = (180, 12)
संख्याओं की अदला-बदली
ध्यान दें कि (A, B) और (B, A) एक ही जोड़ी के रूप में गिनी जाती हैं। इसलिए, हमें केवल अद्वितीय जोड़े गिनने हैं।
अंतिम उत्तर
इस प्रकार, संभावित अद्वितीय जोड़ों की संख्या 2 है:
- (12, 180) और (36, 60)
इसलिए, सही उत्तर विकल्प 'A' है।
दो संख्याओं का H.C.F. 96 है और उनका L.C.M. 1296 है। यदि एक संख्या 864 है, तो दूसरी संख्या क्या होगी?- a)132
- b)135
- c)140
- d)144
Correct answer is option 'D'. Can you explain this answer?
दो संख्याओं का H.C.F. 96 है और उनका L.C.M. 1296 है। यदि एक संख्या 864 है, तो दूसरी संख्या क्या होगी?
a)
132
b)
135
c)
140
d)
144

|
Iq Funda answered |
नियम 1 का उपयोग करते हुए:
1st संख्या × 2nd संख्या = L.C.M. × H.C.F.,
पहली संख्या × दूसरी संख्या = H.C.F. × L.C.M.
⇒ 864 × दूसरी संख्या
= 96 × 1296 ⇒ दूसरी संख्या
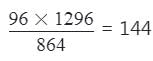
1st संख्या × 2nd संख्या = L.C.M. × H.C.F.,
पहली संख्या × दूसरी संख्या = H.C.F. × L.C.M.
⇒ 864 × दूसरी संख्या
= 96 × 1296 ⇒ दूसरी संख्या
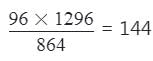
प्रश्न. वह सबसे बड़ा संख्या खोजिए जो 43, 91 और 183 को इस प्रकार विभाजित करेगी कि हर एक में समान शेष बचे।- a)4
- b)7
- c)9
- d)13
Correct answer is option 'A'. Can you explain this answer?
प्रश्न. वह सबसे बड़ा संख्या खोजिए जो 43, 91 और 183 को इस प्रकार विभाजित करेगी कि हर एक में समान शेष बचे।
a)
4
b)
7
c)
9
d)
13

|
Target Study Academy answered |
दी गई संख्याएँ हैं 43, 91, और 183।
सबसे छोटी संख्या को दोनों सबसे बड़ी संख्याओं से घटाइए।
हमारे पास तीन मामले हैं:
183 > 43; 183 > 91 और 91 > 43
इसलिए,
183 – 43 = 140
183 – 91 = 92
91 – 43 = 48
अब, हमारे पास तीन नई संख्याएँ हैं: 140, 48 और 92।
सबसे छोटी संख्या को दोनों सबसे बड़ी संख्याओं से घटाइए।
हमारे पास तीन मामले हैं:
183 > 43; 183 > 91 और 91 > 43
इसलिए,
183 – 43 = 140
183 – 91 = 92
91 – 43 = 48
अब, हमारे पास तीन नई संख्याएँ हैं: 140, 48 और 92।
एचसीएफ (140, 48 और 92) = 4
वह सबसे बड़ी संख्या जो 183, 91, और 43 को विभाजित करती है और समान शेष छोड़ती है, वह है 4।
वह सबसे बड़ी संख्या जो 183, 91, और 43 को विभाजित करती है और समान शेष छोड़ती है, वह है 4।
दो संख्याओं का HCF 23 है और उनके LCM के अन्य दो गुणांक 13 और 14 हैं। दोनों संख्याओं में से बड़ी संख्या क्या है?- a)299
- b)276
- c)322
- d)345
Correct answer is option 'C'. Can you explain this answer?
दो संख्याओं का HCF 23 है और उनके LCM के अन्य दो गुणांक 13 और 14 हैं। दोनों संख्याओं में से बड़ी संख्या क्या है?
a)
299
b)
276
c)
322
d)
345

|
Spectrum Coaching Institute answered |
मान लीजिए संख्याएँ 23x और 23y हैं, जहाँ x और y सह-प्राइम हैं।
∴ LCM = 23xy
जैसा कि दिया गया है,
23xy = 23 × 13 × 14
∴ x = 13, y = 14
∴ बड़ी संख्या = 23y
= 23 × 14 = 322
∴ LCM = 23xy
जैसा कि दिया गया है,
23xy = 23 × 13 × 14
∴ x = 13, y = 14
∴ बड़ी संख्या = 23y
= 23 × 14 = 322
दो संख्याओं का HCF और गुणनफल क्रमशः 15 और 6300 हैं। संख्याओं के संभावित जोड़ों की संख्या कितनी है?- a)3
- b)4
- c)1
- d)2
Correct answer is option 'D'. Can you explain this answer?
दो संख्याओं का HCF और गुणनफल क्रमशः 15 और 6300 हैं। संख्याओं के संभावित जोड़ों की संख्या कितनी है?
a)
3
b)
4
c)
1
d)
2

|
T.S Academy answered |
मान लीजिए कि संख्याएँ 15x और 15y हैं, जहाँ x और y सह-प्राइम हैं।
इसलिए, 15x × 15y = 6300
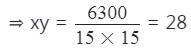
इसलिए, दो जोड़े (7, 4) और (14, 2) हैं।
इसलिए, 15x × 15y = 6300
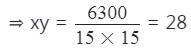
इसलिए, दो जोड़े (7, 4) और (14, 2) हैं।
दो संख्याओं का HCF और LCM क्रमशः 12 और 924 हैं। फिर ऐसी जोड़ों की संख्या क्या है?- a)0
- b)1
- c)2
- d)3
Correct answer is option 'C'. Can you explain this answer?
दो संख्याओं का HCF और LCM क्रमशः 12 और 924 हैं। फिर ऐसी जोड़ों की संख्या क्या है?
a)
0
b)
1
c)
2
d)
3

|
Aim It Academy answered |
दो संख्याओं का HCF और LCM क्रमशः 12 और 924 हैं।
संख्याएँ 12p और 12q मान लेते हैं जहाँ p और q आपस में प्राथमिक हैं।
इसलिए, LCM = 12pq
इसलिए, 12pq = 924
⇒ pq = 77
इसलिए, संभावित जोड़े (1, 77) और (7, 11) हैं।
इसलिए, आवश्यक उत्तर है 2।
संख्याएँ 12p और 12q मान लेते हैं जहाँ p और q आपस में प्राथमिक हैं।
इसलिए, LCM = 12pq
इसलिए, 12pq = 924
⇒ pq = 77
इसलिए, संभावित जोड़े (1, 77) और (7, 11) हैं।
इसलिए, आवश्यक उत्तर है 2।
दो संख्याओं का HCF 15 है और उनका LCM 225 है। यदि एक संख्या 75 है, तो दूसरी संख्या है:- a)90
- b)105
- c)45
- d)60
Correct answer is option 'C'. Can you explain this answer?
दो संख्याओं का HCF 15 है और उनका LCM 225 है। यदि एक संख्या 75 है, तो दूसरी संख्या है:
a)
90
b)
105
c)
45
d)
60

|
Wizius Careers answered |
नियम 1 का उपयोग करते हुए:
1st संख्या × 2nd संख्या = LCM × HCF,
पहली संख्या × दूसरी संख्या = HCF × LCM
⇒ 75 × दूसरी संख्या = 15 × 225
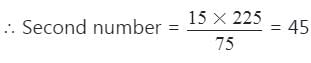
1st संख्या × 2nd संख्या = LCM × HCF,
पहली संख्या × दूसरी संख्या = HCF × LCM
⇒ 75 × दूसरी संख्या = 15 × 225
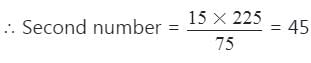
दो संख्याओं का LCM 1920 है और उनका HCF 16 है। यदि एक संख्या 128 है, तो दूसरी संख्या ज्ञात करें।- a)240
- b)204
- c)320
- d)260
Correct answer is option 'A'. Can you explain this answer?
दो संख्याओं का LCM 1920 है और उनका HCF 16 है। यदि एक संख्या 128 है, तो दूसरी संख्या ज्ञात करें।
a)
240
b)
204
c)
320
d)
260

|
Glance Learning Institute answered |
नियम 1 का उपयोग करते हुए:
पहली संख्या × दूसरी संख्या = L.C.M. × H.C.F,
हमारे पास है,
पहली संख्या × दूसरी संख्या = LCM × HCF

पहली संख्या × दूसरी संख्या = L.C.M. × H.C.F,
हमारे पास है,
पहली संख्या × दूसरी संख्या = LCM × HCF

7 का सबसे छोटा गुणांक, जो 6, 9, 15 और 18 से विभाजित करने पर 4 का शेषफल छोड़ता है:- a)74
- b)94
- c)184
- d)364
Correct answer is option 'D'. Can you explain this answer?
7 का सबसे छोटा गुणांक, जो 6, 9, 15 और 18 से विभाजित करने पर 4 का शेषफल छोड़ता है:
a)
74
b)
94
c)
184
d)
364

|
Wizius Careers answered |
6, 9, 15 और 18 का लघुत्तम गुणांक 90 है।
आवश्यक संख्या को 90k + 4 के रूप में मानते हैं, जो 7 का गुणांक है।
(90k + 4) को 7 द्वारा विभाजित करने के लिए k का सबसे छोटा मान 4 है।
अतः आवश्यक संख्या = (90 x 4) + 4 = 364।
आवश्यक संख्या को 90k + 4 के रूप में मानते हैं, जो 7 का गुणांक है।
(90k + 4) को 7 द्वारा विभाजित करने के लिए k का सबसे छोटा मान 4 है।
अतः आवश्यक संख्या = (90 x 4) + 4 = 364।
दो सह-प्राइम संख्याओं का गुणनफल 117 है। तो उनका L.C.M. क्या है?- a)9
- b)117
- c)39
- d)13
Correct answer is option 'B'. Can you explain this answer?
दो सह-प्राइम संख्याओं का गुणनफल 117 है। तो उनका L.C.M. क्या है?
a)
9
b)
117
c)
39
d)
13
|
|
Learnpro Institute answered |
दो सह-प्राइम संख्याओं का HCF = 1
∴ संख्याओं का गुणनफल = उनका L.C.M. = 117
117 = 13 × 9 जहाँ 13 और 9 सह-प्राइम हैं। L.C.M (13,9) = 117।
∴ संख्याओं का गुणनफल = उनका L.C.M. = 117
117 = 13 × 9 जहाँ 13 और 9 सह-प्राइम हैं। L.C.M (13,9) = 117।
मान लीजिए N वह सबसे बड़ी संख्या है जो 1305, 4665 और 6905 को विभाजित करेगी, प्रत्येक मामले में समान शेष छोड़ते हुए। फिर N में अंकों का योगफल है:- a)4
- b)5
- c)6
- d)8
Correct answer is option 'A'. Can you explain this answer?
मान लीजिए N वह सबसे बड़ी संख्या है जो 1305, 4665 और 6905 को विभाजित करेगी, प्रत्येक मामले में समान शेष छोड़ते हुए। फिर N में अंकों का योगफल है:
a)
4
b)
5
c)
6
d)
8

|
Glance Learning Institute answered |
N = वह सबसे बड़ी संख्या है जो 1305, 4665 और 6905 को समान शेष छोड़ते हुए विभाजित करेगी।
⇒ N = (4665 - 1305), (6905 - 4665) और (6905 - 1305) का H.C.F.
⇒ N = 3360, 2240 और 5600 का H.C.F. = 1120
N में अंकों का योगफल = (1 + 1 + 2 + 0) = 4
⇒ N = (4665 - 1305), (6905 - 4665) और (6905 - 1305) का H.C.F.
⇒ N = 3360, 2240 और 5600 का H.C.F. = 1120
N में अंकों का योगफल = (1 + 1 + 2 + 0) = 4
दो संख्याओं का गुणनफल 1280 है और उनका एच.सी.एफ. 8 है। उन संख्याओं का एल.सी.एम. क्या होगा?- a)160
- b)150
- c)120
- d)140
Correct answer is option 'A'. Can you explain this answer?
दो संख्याओं का गुणनफल 1280 है और उनका एच.सी.एफ. 8 है। उन संख्याओं का एल.सी.एम. क्या होगा?
a)
160
b)
150
c)
120
d)
140
|
|
Learnpro Institute answered |
दो संख्याओं का गुणनफल = एच.सी.एफ. × एल.सी.एम.
1280 = 8 × एल.सी.एम.
एल.सी.एम. = 160
1280 = 8 × एल.सी.एम.
एल.सी.एम. = 160
दो 2-अंकीय संख्याओं का H.C.F. और L.C.M. क्रमशः 16 और 480 है। संख्याएँ हैं:- a)60, 72
- b)40, 48
- c)80, 96
- d)64, 80
Correct answer is option 'C'. Can you explain this answer?
दो 2-अंकीय संख्याओं का H.C.F. और L.C.M. क्रमशः 16 और 480 है। संख्याएँ हैं:
a)
60, 72
b)
40, 48
c)
80, 96
d)
64, 80

|
Wizius Careers answered |
नियम 1 का उपयोग करते हुए:
1st संख्या × 2nd संख्या = L.C.M. × H.C.F,
दो 2-अंक की संख्याओं का H.C.F. = 16
इसलिए, संख्याएँ 16x और 16y के रूप में व्यक्त की जा सकती हैं, जहाँ x और y एक-दूसरे के प्रति प्रमुख हैं।
अब,
पहली संख्या × दूसरी संख्या = H.C.F. × L.C.M.
⇒ 16x × 16y = 16 × 480
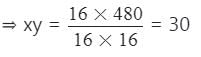
x और y के संभावित युग्म, जो स्थिति xy = 30 को संतुष्ट करते हैं, हैं: (3, 10), (5, 6), (1, 30), (2, 15)
चूंकि संख्याएँ प्रत्येक 2-अंक की हैं।
इसलिए, स्वीकार्य युग्म है (5, 6)
∴ संख्याएँ हैं: 16 × 5 = 80 और 16 × 6 = 96
1st संख्या × 2nd संख्या = L.C.M. × H.C.F,
दो 2-अंक की संख्याओं का H.C.F. = 16
इसलिए, संख्याएँ 16x और 16y के रूप में व्यक्त की जा सकती हैं, जहाँ x और y एक-दूसरे के प्रति प्रमुख हैं।
अब,
पहली संख्या × दूसरी संख्या = H.C.F. × L.C.M.
⇒ 16x × 16y = 16 × 480
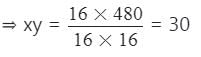
x और y के संभावित युग्म, जो स्थिति xy = 30 को संतुष्ट करते हैं, हैं: (3, 10), (5, 6), (1, 30), (2, 15)
चूंकि संख्याएँ प्रत्येक 2-अंक की हैं।
इसलिए, स्वीकार्य युग्म है (5, 6)
∴ संख्याएँ हैं: 16 × 5 = 80 और 16 × 6 = 96
चार अंकों की सबसे बड़ी संख्या जो 15, 25, 40 और 75 से विभाजित होती है, क्या है?- a)9000
- b)9400
- c)9600
- d)9800
Correct answer is option 'C'. Can you explain this answer?
चार अंकों की सबसे बड़ी संख्या जो 15, 25, 40 और 75 से विभाजित होती है, क्या है?
a)
9000
b)
9400
c)
9600
d)
9800

|
Glance Learning Institute answered |
चार अंकों की सबसे बड़ी संख्या 9999 है।
अब, 15=3×5
25 = 5×5
40 = 2×2×2×5
और 75 = 3×5×5
15, 25, 40 और 75 का L.C.M. है 2×2×2×3×5×5 = 600.
9999 को 600 से विभाजित करने पर, शेषफल 399 है।
आवश्यक संख्या = (9999−399) = 9600.
छह घंटे एक साथ बजना शुरू करते हैं और क्रमशः 2, 4, 6, 8, 10 और 12 सेकंड के अंतराल पर बजते हैं। 30 मिनट में, वे कितनी बार एक साथ बजते हैं?- a)4
- b)10
- c)15
- d)16
Correct answer is option 'D'. Can you explain this answer?
छह घंटे एक साथ बजना शुरू करते हैं और क्रमशः 2, 4, 6, 8, 10 और 12 सेकंड के अंतराल पर बजते हैं। 30 मिनट में, वे कितनी बार एक साथ बजते हैं?
a)
4
b)
10
c)
15
d)
16

|
Glance Learning Institute answered |
समय को 30 मिनट में परिवर्तित करने पर, हमें कुल 1800 सेकंड मिलते हैं। अब, सबसे कम सामान्य गुणांक (LCM) ढूंढना है। घंटियाँ 2, 4, 6, 8, 10 और 12 सेकंड पर बजती हैं। इनका LCM 60 सेकंड होता है। इसका अर्थ है कि वे हर 60 सेकंड (या 1 मिनट) में एक साथ बजते हैं। 30 मिनट में, वे कुल 30 बार एक साथ बजते हैं।
दो संख्याओं का LCM 2079 है और उनका HCF 27 है। यदि एक संख्या 189 है, तो दूसरी संख्या क्या होगी?- a)584
- b)297
- c)216
- d)189
Correct answer is option 'B'. Can you explain this answer?
दो संख्याओं का LCM 2079 है और उनका HCF 27 है। यदि एक संख्या 189 है, तो दूसरी संख्या क्या होगी?
a)
584
b)
297
c)
216
d)
189

|
Glance Learning Institute answered |
नियम 1 का उपयोग करते हुए:
1st संख्या × 2nd संख्या = L.C.M. × H.C.F,
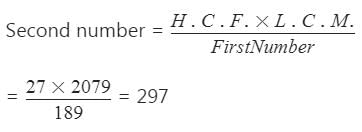
1st संख्या × 2nd संख्या = L.C.M. × H.C.F,
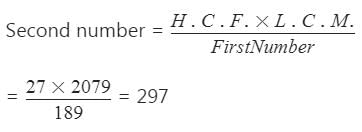
दो संख्याओं का गुणनफल 2160 है और उनका HCF 12 है। ऐसी संभव जोड़ों की संख्या क्या है?- a)1
- b)2
- c)3
- d)4
Correct answer is option 'B'. Can you explain this answer?
दो संख्याओं का गुणनफल 2160 है और उनका HCF 12 है। ऐसी संभव जोड़ों की संख्या क्या है?
a)
1
b)
2
c)
3
d)
4

|
Aim It Academy answered |
HCF = 12
संख्याएँ = 12x और 12y
जहाँ x और y आपस में प्राथमिक हैं।
∴ 12x × 12y = 2160
= 15 = 3 × 5, 1 × 15
संभावित जोड़े = (36, 60) और (12, 180)
इसलिए, ऐसी संभव जोड़ों की संख्या 2 है।
संख्याएँ = 12x और 12y
जहाँ x और y आपस में प्राथमिक हैं।
∴ 12x × 12y = 2160
= 15 = 3 × 5, 1 × 15
संभावित जोड़े = (36, 60) और (12, 180)
इसलिए, ऐसी संभव जोड़ों की संख्या 2 है।
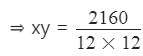
दो संख्याओं का LCM 1920 है और उनका HCF 16 है। यदि एक संख्या 128 है, तो दूसरी संख्या ज्ञात करें।- a)204
- b)240
- c)260
- d)320
Correct answer is option 'B'. Can you explain this answer?
दो संख्याओं का LCM 1920 है और उनका HCF 16 है। यदि एक संख्या 128 है, तो दूसरी संख्या ज्ञात करें।
a)
204
b)
240
c)
260
d)
320

|
Spectrum Coaching Institute answered |
नियम 1 का उपयोग करते हुए:
पहली संख्या × दूसरी संख्या = L.C.M. × H.C.F,
हमें मिलता है,
पहली संख्या × दूसरी संख्या = LCM × HCF
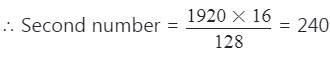
पहली संख्या × दूसरी संख्या = L.C.M. × H.C.F,
हमें मिलता है,
पहली संख्या × दूसरी संख्या = LCM × HCF
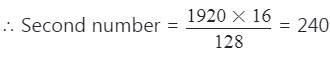
दो संख्याओं का H.C.F. 8 है। निम्नलिखित में से कौन सा उनके L.C.M. का मान कभी नहीं हो सकता?- a)48
- b)24
- c)60
- d)56
Correct answer is option 'C'. Can you explain this answer?
दो संख्याओं का H.C.F. 8 है। निम्नलिखित में से कौन सा उनके L.C.M. का मान कभी नहीं हो सकता?
a)
48
b)
24
c)
60
d)
56

|
T.S Academy answered |
दो संख्याओं का HCF 8 है।
इसका अर्थ है कि 8 दोनों संख्याओं का सामान्य गुणांक है। LCM दोनों संख्याओं का सामान्य गुणनखंड होता है, और यह दोनों संख्याओं द्वारा विभाज्य होता है। इसलिए, अपेक्षित उत्तर = 60
इसका अर्थ है कि 8 दोनों संख्याओं का सामान्य गुणांक है। LCM दोनों संख्याओं का सामान्य गुणनखंड होता है, और यह दोनों संख्याओं द्वारा विभाज्य होता है। इसलिए, अपेक्षित उत्तर = 60
दो संख्याओं का HCF और LCM क्रमशः 13 और 455 है। यदि इनमें से एक संख्या 75 और 125 के बीच है, तो वह संख्या क्या है?- a)91
- b)78
- c)117
- d)104
Correct answer is option 'A'. Can you explain this answer?
दो संख्याओं का HCF और LCM क्रमशः 13 और 455 है। यदि इनमें से एक संख्या 75 और 125 के बीच है, तो वह संख्या क्या है?
a)
91
b)
78
c)
117
d)
104

|
Wizius Careers answered |
HCF = 13
संख्याएँ मान लेते हैं 13x और 13y।
जहाँ x और y सह-प्राइम हैं।
अतः LCM = 13 xy
अतः 13 xy = 455
अतः संख्याएँ हैं 13 × 5 = 65 और 13 × 7 = 91
संख्याएँ मान लेते हैं 13x और 13y।
जहाँ x और y सह-प्राइम हैं।
अतः LCM = 13 xy
अतः 13 xy = 455
अतः संख्याएँ हैं 13 × 5 = 65 और 13 × 7 = 91
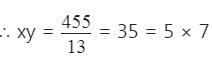
तीन भिन्न संख्याओं का L.C.M. 120 है। निम्नलिखित में से कौन सा उनका H.C.F. नहीं हो सकता?- a)12
- b)8
- c)35
- d)24
Correct answer is option 'C'. Can you explain this answer?
तीन भिन्न संख्याओं का L.C.M. 120 है। निम्नलिखित में से कौन सा उनका H.C.F. नहीं हो सकता?
a)
12
b)
8
c)
35
d)
24

|
Learning Education answered |
L.C.M = 2 × 2 × 2 × 3 × 5
इसलिए, H.C.F = 4, 8, 12 या 24
प्रश्न के अनुसार
35, 120 का H.C.F. नहीं हो सकता।
इसलिए, H.C.F = 4, 8, 12 या 24
प्रश्न के अनुसार
35, 120 का H.C.F. नहीं हो सकता।
दो संख्याओं का LCM उनके HCF का 4 गुना है। LCM और HCF का योग 125 है। यदि एक संख्या 100 है, तो दूसरी संख्या क्या होगी?- a)25
- b)5
- c)125
- d)100
Correct answer is option 'A'. Can you explain this answer?
दो संख्याओं का LCM उनके HCF का 4 गुना है। LCM और HCF का योग 125 है। यदि एक संख्या 100 है, तो दूसरी संख्या क्या होगी?
a)
25
b)
5
c)
125
d)
100

|
Learning Education answered |
नियम 1 का उपयोग करते हुए:
1st संख्या × 2nd संख्या = L.C.M. × H.C.F,
मान लें LCM को L और HCF को H, तो L = 4H
इसलिए H + 4H = 125
=> 5H = 125
=> H = 25
इसलिए L = 4 × 25 = 100
इस प्रकार, दूसरी संख्या 100 होगी।
1st संख्या × 2nd संख्या = L.C.M. × H.C.F,
मान लें LCM को L और HCF को H, तो L = 4H
इसलिए H + 4H = 125
=> 5H = 125
=> H = 25
इसलिए L = 4 × 25 = 100
इस प्रकार, दूसरी संख्या 100 होगी।
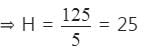
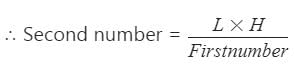
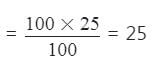
दो संख्याओं का LCM 864 है और उनका HCF 144 है। यदि एक संख्या 288 है, तो दूसरी संख्या क्या होगी?- a)1296
- b)576
- c)144
- d)432
Correct answer is option 'D'. Can you explain this answer?
दो संख्याओं का LCM 864 है और उनका HCF 144 है। यदि एक संख्या 288 है, तो दूसरी संख्या क्या होगी?
a)
1296
b)
576
c)
144
d)
432

|
Wizius Careers answered |
नियम 1 का उपयोग करते हुए:
1वीं संख्या × 2वीं संख्या = L.C.M. × H.C.F,
आवश्यक संख्या

1वीं संख्या × 2वीं संख्या = L.C.M. × H.C.F,
आवश्यक संख्या

दो संख्याओं का H.C.F. 23 है और उनके L.C.M. के अन्य दो गुणांक 13 और 14 हैं। इन दोनों संख्याओं में से बड़ी संख्या क्या है?- a)276
- b)299
- c)322
- d)345
Correct answer is option 'C'. Can you explain this answer?
दो संख्याओं का H.C.F. 23 है और उनके L.C.M. के अन्य दो गुणांक 13 और 14 हैं। इन दोनों संख्याओं में से बड़ी संख्या क्या है?
a)
276
b)
299
c)
322
d)
345

|
T.S Academy answered |
दो संख्याओं का H.C.F. 23 है और L.C.M. के अन्य गुणांक 13 और 14 हैं। इसका अर्थ है कि दोनों संख्याएँ 23, 13 और 14 के गुणनफल का भाग हैं। इस प्रकार, बड़ी संख्या 276 है।
दो संख्याओं का LCM 225 है और उनका HCF 5 है। यदि एक संख्या 25 है, तो दूसरी संख्या क्या होगी?- a)5
- b)25
- c)45
- d)225
Correct answer is option 'C'. Can you explain this answer?
दो संख्याओं का LCM 225 है और उनका HCF 5 है। यदि एक संख्या 25 है, तो दूसरी संख्या क्या होगी?
a)
5
b)
25
c)
45
d)
225

|
Iq Funda answered |
दी गई जानकारी के अनुसार, LCM = 225, HCF = 5,
प्रथम संख्या = 25, द्वितीय संख्या = ?
हम दिए गए सूत्र की मदद से द्वितीय संख्या ज्ञात कर सकते हैं,
“LCM × HCF = 1st Number × 2nd Number”
⇒ 225 × 5 = 25 × द्वितीय संख्या
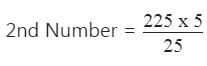
इसलिए, द्वितीय संख्या = 45
प्रथम संख्या = 25, द्वितीय संख्या = ?
हम दिए गए सूत्र की मदद से द्वितीय संख्या ज्ञात कर सकते हैं,
“LCM × HCF = 1st Number × 2nd Number”
⇒ 225 × 5 = 25 × द्वितीय संख्या
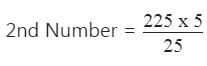
इसलिए, द्वितीय संख्या = 45
दो संख्याओं का HCF 23 है और उनके LCM के अन्य दो गुणांक 13 और 14 हैं। दोनों संख्याओं में से बड़ी संख्या क्या है?- a)276
- b)299
- c)345
- d)322
Correct answer is option 'D'. Can you explain this answer?
दो संख्याओं का HCF 23 है और उनके LCM के अन्य दो गुणांक 13 और 14 हैं। दोनों संख्याओं में से बड़ी संख्या क्या है?
a)
276
b)
299
c)
345
d)
322

|
Iq Funda answered |
HCF 23 है। तो अन्य दो संख्याएँ होंगी,
(23 * 13) और (23 * 14)।
इस प्रकार बड़ी संख्या = 23 * 14 = 322।
(23 * 13) और (23 * 14)।
इस प्रकार बड़ी संख्या = 23 * 14 = 322।
दो संख्याओं का गुणनफल 4107 है। यदि इन संख्याओं का एच.सी.एफ. 37 है, तो बड़ी संख्या क्या होगी?- a)101
- b)107
- c)111
- d)185
Correct answer is option 'C'. Can you explain this answer?
दो संख्याओं का गुणनफल 4107 है। यदि इन संख्याओं का एच.सी.एफ. 37 है, तो बड़ी संख्या क्या होगी?
a)
101
b)
107
c)
111
d)
185

|
Target Study Academy answered |
मान लें कि संख्याएँ 37a और 37b हैं।
तो, 37a x 37b = 4107
 ab = 3।
ab = 3।अब, 3 के साथ सह-प्राइम का उत्पाद (1, 3) है।
इसलिए, आवश्यक संख्याएँ (37 x 1, 37 x 3) अर्थात् (37, 111) हैं।
 बड़ी संख्या = 111।
बड़ी संख्या = 111।दो संख्याओं का HCF 15 है और उनका LCM 300 है। यदि एक संख्या 60 है, तो दूसरी संख्या क्या होगी?- a)75
- b)50
- c)100
- d)65
Correct answer is option 'A'. Can you explain this answer?
दो संख्याओं का HCF 15 है और उनका LCM 300 है। यदि एक संख्या 60 है, तो दूसरी संख्या क्या होगी?
a)
75
b)
50
c)
100
d)
65

|
Learning Education answered |
नियम 1 का उपयोग करते हुए:
1st संख्या × 2nd संख्या = L.C.M. × H.C.F,
पहली संख्या × दूसरी संख्या = HCF × LCM
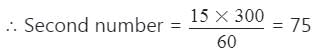
1st संख्या × 2nd संख्या = L.C.M. × H.C.F,
पहली संख्या × दूसरी संख्या = HCF × LCM
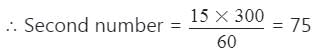
दो संख्याओं का गुणनफल 2028 है और उनका एच.सी.एफ. 13 है। ऐसी जोड़ी की संख्या क्या है?- a)1
- b)2
- c)3
- d)4
Correct answer is option 'B'. Can you explain this answer?
दो संख्याओं का गुणनफल 2028 है और उनका एच.सी.एफ. 13 है। ऐसी जोड़ी की संख्या क्या है?
a)
1
b)
2
c)
3
d)
4
|
|
Learnpro Institute answered |
मान लेते हैं कि संख्याएँ 13a और 13b हैं।
तब, 13a x 13b = 2028
⇒ ab = 12.
दो पूर्णांक a और b को सहज गुणनफल या आपस में सरल कहा जाता है यदि उनका कोई सामान्य सकारात्मक गुणांक 1 के अलावा न हो, या, समान रूप से, यदि उनका सबसे बड़ा सामान्य भाजक 1 हो
अब, 12 का सह-प्रमुख (1, 12) और (3, 4) हैं।
अब, 12 का सह-प्रमुख (1, 12) और (3, 4) हैं।
⇒ आवश्यक संख्याएँ (13 x 1, 13 x 12) और (13 x 3, 13 x 4) हैं।
दो संख्याओं का एच.सी.एफ और एल.सी.एम क्रमशः 12 और 336 है। यदि एक संख्या 84 है, तो दूसरी संख्या क्या होगी?- a)48
- b)36
- c)96
- d)72
Correct answer is option 'A'. Can you explain this answer?
दो संख्याओं का एच.सी.एफ और एल.सी.एम क्रमशः 12 और 336 है। यदि एक संख्या 84 है, तो दूसरी संख्या क्या होगी?
a)
48
b)
36
c)
96
d)
72

|
Glance Learning Institute answered |
नियम 1 का उपयोग करते हुए :
1st संख्या × 2nd संख्या = एल.सी.एम. × एच.सी.एफ,
पहली संख्या × दूसरी संख्या = एच.सी.एफ × एल.सी.एम
⇒ 84 × दूसरी संख्या = 12 × 336
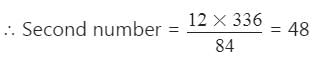
1st संख्या × 2nd संख्या = एल.सी.एम. × एच.सी.एफ,
पहली संख्या × दूसरी संख्या = एच.सी.एफ × एल.सी.एम
⇒ 84 × दूसरी संख्या = 12 × 336
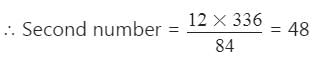
दो संख्याओं का LCM 520 है और उनका HCF 4 है। यदि एक संख्या 52 है, तो दूसरी संख्या क्या होगी?- a)42
- b)40
- c)52
- d)50
Correct answer is option 'B'. Can you explain this answer?
दो संख्याओं का LCM 520 है और उनका HCF 4 है। यदि एक संख्या 52 है, तो दूसरी संख्या क्या होगी?
a)
42
b)
40
c)
52
d)
50

|
Glance Learning Institute answered |
नियम 1 का उपयोग करते हुए:
पहली संख्या × दूसरी संख्या = L.C.M. × H.C.F,
पहली संख्या × दूसरी संख्या = HCF × LCM
⇒ 52 × दूसरी संख्या = 4 × 520
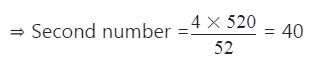
पहली संख्या × दूसरी संख्या = L.C.M. × H.C.F,
पहली संख्या × दूसरी संख्या = HCF × LCM
⇒ 52 × दूसरी संख्या = 4 × 520
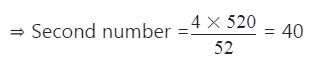
तीन संख्याएँ 3 : 4 : 5 के अनुपात में हैं और उनका L.C.M. 2400 है। उनकी H.C.F. क्या है?- a)40
- b)80
- c)120
- d)200
Correct answer is option 'A'. Can you explain this answer?
तीन संख्याएँ 3 : 4 : 5 के अनुपात में हैं और उनका L.C.M. 2400 है। उनकी H.C.F. क्या है?
a)
40
b)
80
c)
120
d)
200

|
Spectrum Coaching Institute answered |
तीन संख्याओं का L.C.M. 2400 है। चूंकि ये संख्याएँ 3 : 4 : 5 के अनुपात में हैं, हम H.C.F. की गणना कर सकते हैं। H.C.F. = L.C.M. / (a*b*c) जहां a, b, और c अनुपात के गुणांक हैं। यहाँ, H.C.F. = 2400 / (3 * 4 * 5) = 2400 / 60 = 40।
दो संख्याओं का गुणनफल 2028 और उनका HCF 13 है। ऐसे जोड़ों की संख्या क्या है?- a)2
- b)1
- c)4
- d)3
Correct answer is option 'A'. Can you explain this answer?
दो संख्याओं का गुणनफल 2028 और उनका HCF 13 है। ऐसे जोड़ों की संख्या क्या है?
a)
2
b)
1
c)
4
d)
3

|
T.S Academy answered |
यहाँ, HCF = 13
संख्याएँ 13x और 13y मानें जहाँ x और y एक-दूसरे के प्रति अभाज्य हैं।
अब, 13x × 13y = 2028
संभावित जोड़ियाँ हैं : (1, 12), (3, 4), (2, 6)
लेकिन 2 और 6 अभाज्य नहीं हैं।
अतः आवश्यक जोड़ियों की संख्या = 2
संख्याएँ 13x और 13y मानें जहाँ x और y एक-दूसरे के प्रति अभाज्य हैं।
अब, 13x × 13y = 2028
संभावित जोड़ियाँ हैं : (1, 12), (3, 4), (2, 6)
लेकिन 2 और 6 अभाज्य नहीं हैं।
अतः आवश्यक जोड़ियों की संख्या = 2
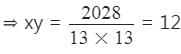
तीन भिन्न संख्याओं का L.C.M. 120 है। निम्नलिखित में से कौन सा उनके H.C.F. नहीं हो सकता?- a)8
- b)12
- c)24
- d)35
Correct answer is option 'D'. Can you explain this answer?
तीन भिन्न संख्याओं का L.C.M. 120 है। निम्नलिखित में से कौन सा उनके H.C.F. नहीं हो सकता?
a)
8
b)
12
c)
24
d)
35

|
Wizius Careers answered |
हमें पता है कि:
L.C.M. दी गई संख्याओं का सबसे छोटा सामान्य गुणनखंड है जबकि H.C.F. उन संख्याओं का सबसे बड़ा सामान्य गुणांक है।
फिर, L.C.M. एक सामान्य गुणांक और संख्याओं के अन्य भिन्न गुणांक के गुणनफल के रूप में है।
L.C.M. = 120 को गुणनांकित रूप में लिखें, अर्थात्
120 = 2 × 2 × 2 × 3 × 5
= 4(2 × 3 × 5)
⇒ 4 संख्याओं का सामान्य गुणांक है।
इसलिए, तीन संख्याओं का H.C.F. 4 का गुणांक है।
4 के गुणांक: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, ...
इसलिए, 35 4 का गुणांक नहीं है, इसलिए 35 उनके H.C.F. नहीं हो सकता।
L.C.M. दी गई संख्याओं का सबसे छोटा सामान्य गुणनखंड है जबकि H.C.F. उन संख्याओं का सबसे बड़ा सामान्य गुणांक है।
फिर, L.C.M. एक सामान्य गुणांक और संख्याओं के अन्य भिन्न गुणांक के गुणनफल के रूप में है।
L.C.M. = 120 को गुणनांकित रूप में लिखें, अर्थात्
120 = 2 × 2 × 2 × 3 × 5
= 4(2 × 3 × 5)
⇒ 4 संख्याओं का सामान्य गुणांक है।
इसलिए, तीन संख्याओं का H.C.F. 4 का गुणांक है।
4 के गुणांक: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, ...
इसलिए, 35 4 का गुणांक नहीं है, इसलिए 35 उनके H.C.F. नहीं हो सकता।
दो संख्याओं का HCF 16 है और उनका LCM 160 है। यदि एक संख्या 32 है, तो दूसरी संख्या क्या होगी?- a)80
- b)48
- c)112
- d)96
Correct answer is option 'A'. Can you explain this answer?
दो संख्याओं का HCF 16 है और उनका LCM 160 है। यदि एक संख्या 32 है, तो दूसरी संख्या क्या होगी?
a)
80
b)
48
c)
112
d)
96

|
Target Study Academy answered |
नियम 1 का उपयोग करते हुए:
1st संख्या × 2nd संख्या = L.C.M. × H.C.F,
हमें पता है कि,
पहली संख्या × दूसरी संख्या = LCM × HCF
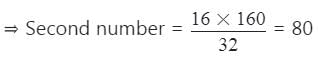
1st संख्या × 2nd संख्या = L.C.M. × H.C.F,
हमें पता है कि,
पहली संख्या × दूसरी संख्या = LCM × HCF
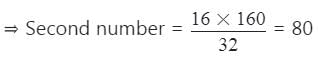
1.08, 0.36 और 0.9 का सबसे बड़ा सामान्य भाजक क्या है?- a)0.03
- b)0.9
- c)0.18
- d)0.108
Correct answer is option 'C'. Can you explain this answer?
1.08, 0.36 और 0.9 का सबसे बड़ा सामान्य भाजक क्या है?
a)
0.03
b)
0.9
c)
0.18
d)
0.108

|
Learning Education answered |
दी गई संख्याएँ हैं 1.08, 0.36 और 0.90
G.C.D. अर्थात् H.C.F 108, 36 और 90 का 18 है
इसलिए, दी गई संख्याओं का H.C.F = 0.18
G.C.D. अर्थात् H.C.F 108, 36 और 90 का 18 है
इसलिए, दी गई संख्याओं का H.C.F = 0.18
दो संख्याओं का गुणनफल 216 है। यदि उनका HCF 6 है, तो उनका LCM क्या होगा?- a)60
- b)72
- c)36
- d)48
Correct answer is option 'C'. Can you explain this answer?
दो संख्याओं का गुणनफल 216 है। यदि उनका HCF 6 है, तो उनका LCM क्या होगा?
a)
60
b)
72
c)
36
d)
48

|
Spectrum Coaching Institute answered |
मान लीजिए कि संख्याएँ 6x और 6y हैं जहाँ x और y एक-दूसरे के लिए प्राइम हैं।
∴ 6x × 6y = 216
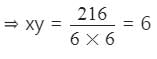
∴ LCM = 6xy = 6 × 6 = 36
∴ 6x × 6y = 216
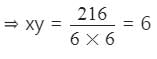
∴ LCM = 6xy = 6 × 6 = 36
दो संख्याओं का HCF 15 है और उनका LCM 225 है। यदि इनमें से एक संख्या 75 है, तो दूसरी संख्या क्या होगी?- a)105
- b)90
- c)60
- d)45
Correct answer is option 'D'. Can you explain this answer?
दो संख्याओं का HCF 15 है और उनका LCM 225 है। यदि इनमें से एक संख्या 75 है, तो दूसरी संख्या क्या होगी?
a)
105
b)
90
c)
60
d)
45
|
|
Learnpro Institute answered |
पहली संख्या x दूसरी संख्या = HCF x LCM
फिर, 75 x दूसरी संख्या = 15 x 225
दूसरी संख्या = {15 x 225}/75 = 45
इसलिए, दूसरी संख्या 45 है।
फिर, 75 x दूसरी संख्या = 15 x 225
दूसरी संख्या = {15 x 225}/75 = 45
इसलिए, दूसरी संख्या 45 है।
दो संख्याओं का HCF और LCM क्रमशः 18 और 378 है। यदि एक संख्या 54 है, तो दूसरी संख्या क्या होगी?- a)144
- b)126
- c)238
- d)198
Correct answer is option 'B'. Can you explain this answer?
दो संख्याओं का HCF और LCM क्रमशः 18 और 378 है। यदि एक संख्या 54 है, तो दूसरी संख्या क्या होगी?
a)
144
b)
126
c)
238
d)
198

|
Learning Education answered |
नियम 1 का उपयोग करते हुए :
1st संख्या × 2nd संख्या = LCM × HCF,

1st संख्या × 2nd संख्या = LCM × HCF,

दो संख्याओं का गुणनफल 4107 है। यदि संख्याओं का उच्चतम सामान्य भाजक (H.C.F.) 37 है, तो बड़ी संख्या क्या है?- a)111
- b)185
- c)101
- d)107
Correct answer is option 'A'. Can you explain this answer?
दो संख्याओं का गुणनफल 4107 है। यदि संख्याओं का उच्चतम सामान्य भाजक (H.C.F.) 37 है, तो बड़ी संख्या क्या है?
a)
111
b)
185
c)
101
d)
107

|
Iq Funda answered |
नियम 1 का उपयोग करते हुए:
1st संख्या × 2nd संख्या = L.C.M. × H.C.F.,
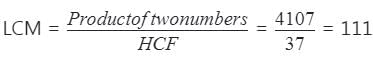
स्पष्ट है कि संख्याएँ 111 और 37 हैं जो दिए गए शर्त को संतुष्ट करती हैं।
इसलिए, बड़ी संख्या = 111
1st संख्या × 2nd संख्या = L.C.M. × H.C.F.,
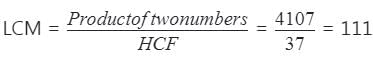
स्पष्ट है कि संख्याएँ 111 और 37 हैं जो दिए गए शर्त को संतुष्ट करती हैं।
इसलिए, बड़ी संख्या = 111
Chapter doubts & questions for एचसीएफ और एलसीएम (HCF & LCM) - SSC CGL Tier 2 - Study Material, Online Tests, Previous Year (Hindi) 2025 is part of SSC CGL exam preparation. The chapters have been prepared according to the SSC CGL exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for SSC CGL 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of एचसीएफ और एलसीएम (HCF & LCM) - SSC CGL Tier 2 - Study Material, Online Tests, Previous Year (Hindi) in English & Hindi are available as part of SSC CGL exam.
Download more important topics, notes, lectures and mock test series for SSC CGL Exam by signing up for free.
SSC CGL Tier 2 - Study Material, Online Tests, Previous Year (Hindi)
374 videos|1072 docs|1174 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup









