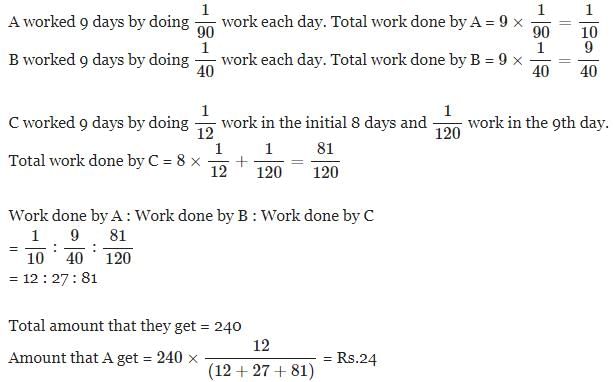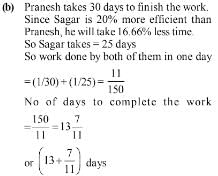अभ्यास परीक्षण: समय और कार्य - 2 - UPSC MCQ
20 Questions MCQ Test - अभ्यास परीक्षण: समय और कार्य - 2
मयंक एक ही समय में शिशु से 50% अधिक कार्य कर सकता है। शिशु अकेले एक कार्य को 30 घंटे में कर सकता है। शिशु काम करना शुरू करता है और जब मयंक उसके साथ जुड़ता है, तब उसने पहले ही 12 घंटे काम किया होता है। शिशु और मयंक को मिलकर बचे हुए कार्य को पूरा करने के लिए कितने घंटे काम करना चाहिए?
A एक कार्य 90 दिन में, B 40 दिन में और C 12 दिन में कर सकता है। वे बारी-बारी से, अर्थात् पहले दिन A अकेले काम करता है, दूसरे दिन B अकेले काम करता है और तीसरे दिन C अकेले काम करता है। इसके बाद यह चक्र तब तक दोहराया जाता है जब तक कार्य पूरा नहीं हो जाता। उन्हें इस काम के लिए 240 रुपये मिलते हैं। यदि मजदूरी को उनके द्वारा किए गए कार्य के अनुपात में बांटा जाए। A को कितना धन मिलेगा?
नीचे दिए गए अनुच्छेद को पढ़ें और इसके आधार पर प्रश्नों का उत्तर दें।
एक जल आपूर्ति स्टेशन पर टैंक को कई पंपों द्वारा पानी से भरा जाता है। पहले तीन समान क्षमता के पंप चालू किए जाते हैं: 2.5 घंटे बाद, दो और पंप (दोनों समान) विभिन्न क्षमता के चालू किए जाते हैं। 1 घंटे बाद, अतिरिक्त पंप चालू किए गए; टैंक लगभग अपनी क्षमता तक भर गया था (15 म3 अभी भी कम थे): एक और घंटे में टैंक भर गया। अतिरिक्त में से एक पंप टैंक को 40 घंटों में भर सकता था।
प्रश्न: टैंक की मात्रा क्या है?
एक जल आपूर्ति स्टेशन पर टैंक को कई पंपों द्वारा पानी से भरा जाता है। पहले तीन समान क्षमता के पंप चालू किए जाते हैं: 2.5 घंटे बाद, दो और पंप (दोनों समान) विभिन्न क्षमता के चालू किए जाते हैं। 1 घंटे बाद, अतिरिक्त पंप चालू किए गए; टैंक लगभग अपनी क्षमता तक भर गया था (15 म3 अभी भी कम थे): एक और घंटे में टैंक भर गया। अतिरिक्त में से एक पंप टैंक को 40 घंटों में भर सकता था।
नीचे दिए गए अनुच्छेद को पढ़ें और इसके आधार पर प्रश्नों का उत्तर दें।
तीन नल A, B और C और एक आउटलेट पाइप D हैं। A, B और C क्रमशः 10, 20 और 25 घंटे में टैंक भर सकते हैं। आउटलेट पाइप उसी टैंक को 100 घंटे में खाली कर सकता है। क्षेत्र में 2,000 घर हैं। टैंक की क्षमता 50,000 लीटर है।
प्रश्न।
यदि सभी नल और आउटलेट पाइप एक साथ खोले जाएं, तो हर घंटे टैंक में कितना पानी डाला जाएगा?
एक टैंक में तीन नल A, B और C हैं। ये क्रमशः 25 घंटे, 20 घंटे और 10 घंटे में टैंक भर सकते हैं। पहले, सभी नल एक साथ खोले जाते हैं। फिर 1 घंटे के बाद, नल C बंद कर दिया जाता है और नल A और B चालू रहते हैं। चौथे घंटे के बाद, नल B भी बंद कर दिया जाता है। शेष कार्य नल A अकेले करता है।
नल A द्वारा स्वयं किए गए कार्य का प्रतिशत ज्ञात करें?
अणुप एक कुआं 10 दिनों में खोद सकता है। लेकिन विशेष रूप से कठिन समय में कार्य ऐसा होता है कि थकान के कारण प्रत्येक अगले दिन एक श्रमिक की क्षमता 10% गिर जाती है। यदि अणुप को कठिन समय में एक ऐसा कुआं खोदने का कार्य दिया जाता है, तो वह इसे कितने दिनों में पूरा करेगा?
A और B मिलकर एक काम 3 दिन में पूरा कर सकते हैं। वे साथ में शुरू करते हैं लेकिन 2 दिन बाद, B काम छोड़ देता है। यदि काम दो और दिनों में पूरा होता है, तो B अकेले इस काम को कितने दिन में पूरा कर सकता है?
नीचे दिए गए डेटा को देखें और निम्नलिखित प्रश्नों का उत्तर दें।
अनूप DOG प्रवेश परीक्षा में पढ़ाई समझने के खंड लिख रहा था। चार पैसों के चारों के पास चारों के पास एक समान लंबाई थी, जिसमें चार पैसों के बाद क्रमशः 5, 8, 8 और 6 प्रश्न थे। यह ज्ञात है कि अनूप किसी भी चारों पैसों को पढ़ने में जितना समय लेता है, उतनी ही समय में वह ठीक 12 प्रश्नों का उत्तर दे सकता है। मान लें कि उसके पढ़ने और प्रश्नों का उत्तर देने की दर पूरे खंड में समान रहती है।
प्र.
अनूप को अपनी पढ़ने की गति कितने प्रतिशत बढ़ानी चाहिए यदि उसे इस खंड पर व्यतीत कुल समय को 20% कम करना है? मान लें कि प्रश्नों का उत्तर देने में व्यतीत समय स्थिर है और निर्देशों में जैसा दिया गया है।
A, B और C मिलकर एक काम को 30 दिनों में पूरा करते हैं। A B की तुलना में दो गुना तेजी से काम कर सकता है। A और C मिलकर B की तुलना में तीन गुना तेजी से काम कर सकते हैं। यदि A, B और C मिलकर एक काम को पूरा करते हैं, तो प्रत्येक व्यक्ति काम को कितने दिनों में पूरा कर सकता है?
यदि सबसे बड़े पाइप से केवल 49 मिनट में एक टंकी भरती है, तो 1 सेमी, 2 सेमी और 3 सेमी व्यास वाले तीन पाइपों द्वारा टंकी कितने समय में भरी जाएगी, यदि प्रत्येक पाइप से बहने वाले पानी की मात्रा उसके व्यास के वर्ग के अनुपात में है?
Sagar Pranesh से 20% अधिक कुशल है। यदि Pranesh एक कार्य को 30 दिनों में पूरा कर सकता है, तो Sagar और Pranesh मिलकर वह कार्य कितने दिनों में पूरा करेंगे?
एक फैक्ट्री रंग बनाने का काम करती है। इसमें 12 पुरुष और दो मशीनें हैं जिन्हें इसके सभी पुरुष संचालित कर सकते हैं। एक रंग को मशीन पर संचालक के साथ बनाने में 4 घंटे लगते हैं। मशीनें बिना ब्रेक के लगातार काम कर सकती हैं। मशीन के बिना प्रत्येक पुरुष एक रंग बनाने में 8 घंटे लेता है। नीति ऐसी है कि उत्पादन अधिकतम किया जाए और पुरुष तीन शिफ्टों में 8 घंटे प्रति दिन काम करने के लिए तैयार हैं। यदि 1 पुरुष घंटे की लागत 20 रुपये है और 1 मशीन घंटे की लागत 15 रुपये है, तो प्रति रंग औसत लागत क्या होगी?
480 व्यक्ति जो प्रतिदिन 10 घंटे काम करते हैं, 10 दिनों में काम का एक चौथाई पूरा करते हैं। शेष काम को 20 दिनों में, प्रतिदिन 8 घंटे काम करके पूरा करने के लिए कितने अतिरिक्त व्यक्तियों की आवश्यकता है?
अनिल, भुवन और चंदन एक काम पूरा करने में क्रमशः 10, 20 और 25 दिन लेते हैं। यदि एक ही दिन में इनमें से दो से अधिक लोग एक साथ काम नहीं करते हैं और कोई भी दो लगातार दिनों में एक ही जोड़ी काम नहीं करती है, तो काम पूरा करने के लिए न्यूनतम समय क्या आवश्यक है?
अनुज एक निश्चित संख्या में दिनों में एक कार्य कर सकता है। उसी कार्य को करने के लिए, भानु अनुज द्वारा लिए गए दिनों की तीन गुना संख्या लेता है, जबकि चंदू भानु द्वारा लिए गए दिनों की तीन गुना संख्या लेता है और डोडो चंदू द्वारा लिए गए दिनों की तीन गुना संख्या लेता है। अब, उन्हें जोड़ा गया है और दो समूह बनाए गए हैं। पहला जोड़ा दूसरे जोड़े द्वारा कार्य को पूरा करने के लिए लिए गए समय का एक-तिहाई समय लेता है, तो पहला जोड़ा कौन है?
दो पाइप अलग-अलग 20 घंटे और 30 घंटे में एक टैंक भर सकते हैं। दोनों पाइप टैंक भरने के लिए खोले जाते हैं लेकिन जब टैंक 3/4था भरा होता है, तो एक रिसाव विकसित होता है, जिससे दोनों पाइपों द्वारा आपूर्ति किए गए पानी का एक चौथाई बाहर चला जाता है। टैंक भरने में कुल समय कितना लगता है?
एक टैंक को 20 पंपों द्वारा 30 मिनट में भरा जा सकता है। यदि पांच पंप खराब हो जाते हैं, तो शेष पंपों द्वारा इसे भरने में कितना समय लगेगा?
एक सैन्य शिविर में 200 सैनिकों के लिए 40 दिनों का पर्याप्त भोजन है। 10 दिनों के बाद, कुछ सैनिक शामिल होते हैं और हर कोई पहले से 50% अधिक खाता है। अब भोजन अगले 10 दिनों के लिए चलता है। 10 दिनों के बाद शिविर में कितने सैनिक शामिल हुए?
एक आदमी, एक महिला या एक लड़का क्रमशः 20 दिनों, 30 दिनों या 60 दिनों में काम कर सकते हैं। 4 पुरुषों और 5 महिलाओं की सहायता के लिए कितने लड़कों की आवश्यकता होगी ताकि वे 2 दिनों में काम पूरा कर सकें?
अकेले काम करते समय, अनु, तानु और मनु द्वारा किसी भी काम को पूरा करने का समय 5 : 8 : 10 के अनुपात में है। वे एक ऐसा काम स्वीकार करते हैं जिसे वे सभी मिलकर 4 दिन में 8 घंटे प्रति दिन काम करके समाप्त कर सकते हैं। हालांकि, अनु और तानु पहले 6 दिनों के लिए एक साथ काम करते हैं, जो कि 6 घंटे 40 मिनट प्रति दिन है। फिर, मनु को अकेले शेष काम पूरा करने में कितने घंटे लगेंगे?



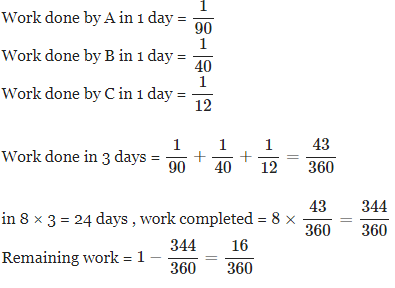 .
.