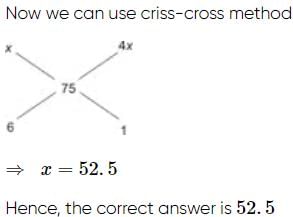
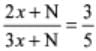महत्वपूर्ण प्रश्न परीक्षण: अनुपात और समानुपात - 2 - UPSC MCQ
15 Questions MCQ Test CSAT की तैयारी (हिंदी) - महत्वपूर्ण प्रश्न परीक्षण: अनुपात और समानुपात - 2
एक क्षेत्र के द्वारा बनाए गए कोण की डिग्री क्या है, जिसका क्षेत्रफल अर्धवृत्त के क्षेत्रफल के साथ अनुपात 1:10 के बराबर है?
हीरे का मूल्य इसके वजन के वर्ग के समानुपाती होता है। यदि एक हीरा जिसकी कीमत ₹10,000 है, को 4:6 के अनुपात में 2 टुकड़ों में बांटा जाता है, तो मूल्य में कमी कितनी होगी?
दो रेलवे स्टेशनों, पटना और लखनऊ के बीच पहले, दूसरे और तीसरे श्रेणी के किराए का अनुपात 10:8:3 है और दोनों स्टेशनों के बीच पहले, दूसरे और तीसरे श्रेणी के यात्रियों की संख्या का अनुपात 3:4:10 है। यदि टिकट की कुल बिक्री 16,100 रुपये है, तो दूसरे श्रेणी के टिकटों की बिक्री से प्राप्त राशि ज्ञात कीजिए।
दो घोड़े की कीमत 5 कुत्तों के बराबर है, 6 कुत्तों की कीमत 8 बैल के बराबर है, 10 बैल की कीमत 50 भेड़ों के बराबर है, और 14 भेड़ों की कीमत 9 बकरियों के बराबर है। यदि एक बकरी की कीमत 70 रुपये है, तो एक घोड़े की कीमत कितनी होगी?
A बी के समानुपाती है। बी सी के विपरीत समानुपाती है। सी डी के वर्ग के समानुपाती है। डी ई के घनमूल के सीधे समानुपाती है। सकारात्मक पूर्णांकों को मानते हुए, यदि A बढ़ता है तो E
चार संख्याओं का योग 253 है। पहली संख्या और दूसरी संख्या का अनुपात 2:3 है। दूसरी संख्या और तीसरी संख्या का अनुपात 5:6 है। तीसरी संख्या और चौथी संख्या का अनुपात 8:9 है। दूसरी संख्या और तीसरी संख्या का औसत क्या है?
एक आदमी के पास एक-रुपये, पांच-रुपये और दस-रुपये के नोटों में 480 रुपये हैं। प्रत्येक संप्रदाय के नोटों की संख्या समान है। उसके पास कुल कितने नोट हैं?
तीन मित्र A, B और C ने 4:1:15 के अनुपात में पूंजी के साथ एक उद्यम शुरू किया। हर तिमाही के अंत में A अपनी पूंजी को आधा कर देता है, जबकि B अपनी पूंजी को दोगुना कर देता है और C अपनी पूंजी को अप्रभावित रखता है। यह प्रक्रिया वर्ष के अंत तक दोहराई जाती है। यदि वर्ष के अंत में B के लाभ का हिस्सा 22,000 रुपये है, तो कुल लाभ क्या है?
गांधिजी के पास गायें हैं, कुछ काली और कुछ सफेद। उन्हें पता चलता है कि 4 काली गायें और 3 सफेद गायें 5 दिनों में उतना दूध देती हैं जितना 3 काली गायें और 5 सफेद गायें 4 दिनों में देती हैं। एक काली गाय द्वारा एक दिन में दिए गए दूध का अनुपात एक सफेद गाय द्वारा दिए गए दूध के अनुपात के लिए क्या है?
एक धातु व्यापारी 2 प्रकार की चांदी की पन्नियों को खरीदता है, जिनकी कीमतों का अनुपात 1:4 है। वह मिश्र धातु को प्रति किलोग्राम 90 रुपये में बेचता है ताकि उसे 20% का लाभ हो सके। यदि मिश्र धातु में उपस्थित उनकी मात्रा का अनुपात क्रमशः 6:1 है, तो कम मात्रा में उपस्थित पन्नी की खरीद मूल्य ज्ञात करें।
नीचे दिए गए अनुच्छेद को पढ़ें और इसके आधार पर प्रश्नों का उत्तर दें।
एक पुस्तक जिसमें 4,000 से 5,000 पन्ने हैं, उसे चार भागों में विभाजित किया गया है, प्रत्येक भाग को अध्यायों में विभाजित किया गया है। चारों भागों में कुल पन्नों की संख्या समान है। चारों भागों में अध्यायों का अनुपात 6:5:10:14 है। चौथे भाग में अध्यायों की संख्या 70 है।
सीता और उसकी माँ की उम्र का अनुपात 2:3 है। N वर्षों बाद, उनकी उम्र का अनुपात 3:5 हो जाएगा। N का मान क्या है?
P, Q से दो गुना तेज़ काम करता है, जबकि P और Q मिलकर R से तीन गुना तेज़ काम कर सकते हैं। यदि P, Q और R मिलकर एक कार्य करते हैं, तो उन्हें आय का अनुपात किस प्रकार बांटना चाहिए?
नीचे दिए गए अंश को पढ़ें और इसके आधार पर प्रश्नों का उत्तर दें।
एक टोकरी में कुछ मात्रा में सेब, अमरूद और संतरे हैं। प्रत्येक किस्म की संख्या एक से अधिक है। सेबों की संख्या और अमरूदों की संख्या का अनुपात अमरूदों की संख्या और संतरे की संख्या के अनुपात के बराबर है।
प्रश्न।
यदि फलों की कुल संख्या 61 है, तो अमरूदों की संख्या ज्ञात करें।
एक व्यक्ति के पास 25 पैसे, 50 पैसे और 1 रुपये के सिक्के हैं। कुल 220 सिक्के हैं और कुल राशि 160 रुपये है। यदि 25 पैसे के सिक्कों की तुलना में 1 रुपये के सिक्कों की संख्या तीन गुना है, तो 50 पैसे के सिक्कों की संख्या क्या है?
|
67 videos|98 docs|119 tests
|