Test: Problem Solving- 3 - UPSC MCQ
15 Questions MCQ Test CSAT Preparation - Test: Problem Solving- 3
6 students of nursery class are playing a game. They are standing in a circle and have to pass a ball among themselves. How many such passes are possible?
There are 5 boys standing in a row and 5 girls are to be paired with them for a group dance competition in a school. In how many ways can the girls be made to stand?
In the editorial group’s photograph of a school all the 5 teachers are to be seated in the front row. Four girls are to be in the second row and six boys in the third row. If the principal has a fixed seat in the first row, then how many arrangements are possible?
In how many ways can 8 people be seated at a round table?
Sunita wants to make a necklace. She has 8 beads. How many different choices does she have?
From city A to B there are 3 different roads. From B to C there are 5. From C to D there are 2. Laxman has to go from city A to D attending some work in city B and C on the way and has to come back in the reverse order. In how many ways can he complete his journey if he has to take a different while coming back than he did while going?
Neetu has five identical beads each of nine different colours. She wants to make a necklace such that the beads of the same colour always come together. How many different arrangements can she have?
On a chess board one white square is chosen at random. In how many ways can a black square be chosen such that it does not lie in the same row as the white square?
How many necklaces can be made using at least 5 from 8 beads of different colours?
Using all the prime numbers less than 10 how many four-digit even numbers can be made if repetition is not allowed?
There are 15 points in a plane, out of which 6 are collinear. How many pentagons can be drawn with these points?
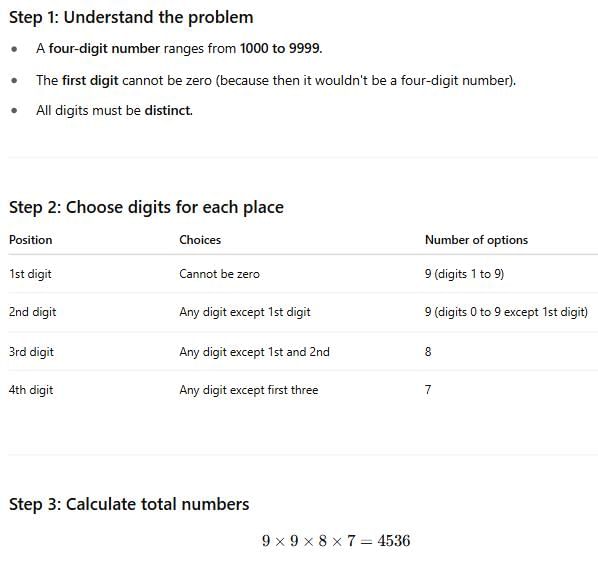
How many four-digit numbers are there with distinct digits?
In how many ways can 9 students be seated in a row such that the tallest child and the shortest child never sit together?
|
207 videos|265 docs|138 tests
|