Test: Bending Moment & Shear Force Diagram - 2 - Mechanical Engineering MCQ
30 Questions MCQ Test GATE Mechanical (ME) Mock Test Series 2026 - Test: Bending Moment & Shear Force Diagram - 2
The shear force in a beam subjected to pure positive bending is…… (positive/zero/negative)
A beam is made up of two identical bars AB and BC, by hinging them together at B. The end A is built-in (cantilevered) and the end C is simply-supported. With the load P acting as shown, the bending moment at A is:
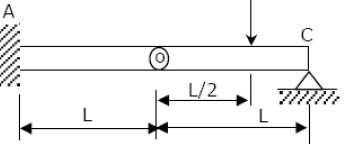
A simply supported beam carries a load 'P' through a bracket, as shown in Figure. The maximum bending moment in the beam is
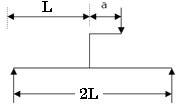
A mass less beam has a loading pattern as shown in the figure. The beam is of rectangular cross -section with a width of 30 mm and height of 100 mm.
The maximum magnitude of bending stress (in MPa) is given by
Solve the problems and choose correct answers A steel beam of breadth 120 mm and height 750 mm is loaded as shown in the figure. Assume Esteel= 200 GPa.
The value of maximum deflection of the beam is:
A simply supported beam of span length 6m and 75mm diameter carries a uniformly distributed load of 1.5 kN/m
What is the maximum value of bending stress?
A simply supported beam of length 'l' is subjected to a symmetrical uniformly varying load with zero intensity at the ends and intensity w (load per unit length) at the mid span. What is the maximum bending moment?
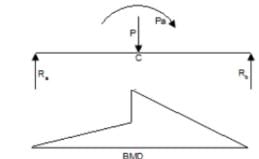
A beam subjected to a load P is shown in the given figure. The bending moment at the support AA of the beam will be
A rectangular section beam subjected to a bending moment M varying along its length is required to develop same maximum bending stress at any cross-section. If the depth of the section is constant, then its width will vary as
A cantilever beam having 5 m length is so loaded that it develops a shearing force of 20T and a bending moment of 20 T-m at a section 2m from the free end. Maximum shearing force and maximum bending moment developed in the beam under this load are respectively 50 T and 125 T-m. The load on the beam is:
A cantilever beam of 2m length supports a triangularly distributed load over its entire length, the maximum of which is at the free end. The total load is 37.5 kN.What is the bending moment at the fixed end?
Assertion (A): If the bending moment diagram is a rectangle, it indicates that the beam is loaded by a uniformly distributed moment all along the length.
Reason (R): The BMD is a representation of internal forces in the beam and not the moment applied on the beam.
A simply supported beam is loaded as shown in the above figure. The maximum shear force in the beam will be
Constant bending moment over span "l " will occur in
A beam is simply supported at its ends and is loaded by a couple at its mid -span as shown in figure A. Shear force diagram for the beam is given by the figure.
A beam having uniform cross-section carries a uniformly distributed load of intensity q per unit length over its entire span, and its mid-span deflection is δ.
The value of mid-span deflection of the same beam when the same load is distributed with intensity varying from 2q unit length at one end to zero at the other end is:
The bending moment diagram shown in Fig. I correspond to the shear force diagram in
Figure shown above represents the BM diagram for a simply supported beam. The beam is subjected to which one of the following?
The figure given below shows a bending moment diagram for the beam CABD:
Load diagram for the above beam will be:
Which one of the following is NOT a statically indeterminate structure?
Assertion (A): The change in bending moment between two cross-sections of a beam is equal to the area of the shearing force diagram between the two sections.
Reason (R): The change in the shearing force between two cross-sections of beam due to distributed loading is equal to the area of the load intensity diagram between the two sections.
A load perpendicular to the plane of the handle is applied at the free end as shown in the given figure. The values of Shear Forces (S.F.), Bending Moment (B.M.) and torque at the fixed end of the handle have been determined respectively as 400 N, 340 Nm and 100 by a student. Among these values, those of
The beam is loaded as shown in Fig. I. Select the correct B.M. diagram
For the shear force to be uniform throughout the span of a simply supported beam, it should carry which one of the following loadings?
Which one of the following figures represents the correct shear force diagram for the loaded beam shown in the given figure I?
A simply supported beam of span l is subjected to a uniformly varying load having zero intensity at the left support and w N/m at the right support. The reaction at the right support is:
A point, along the length of a beam subjected to loads, where bending moment changes its sign, is known as the point of
The shear force diagram of a loaded beam is shown in the following figure: The maximum Bending Moment of the beam is:
The bending moment diagram for a simply supported beam is a rectangle over a larger portion of the span except near the supports. What type of load does the beam carry?
Assertion (A): In a loaded beam, if the shear force diagram is a straight line parallel to the beam axis, then the bending moment is a straight line inclined to the beam axis.
Reason (R): When shear force at any section of a beam is zero or changes sign, the bending moment at that section is maximum.
|
30 docs|220 tests
|