Analytical Reasoning Practice Quiz - 1 - UPSC MCQ
10 Questions MCQ Test UPSC Prelims Paper 2 CSAT - Quant, Verbal & Decision Making - Analytical Reasoning Practice Quiz - 1
Find the minimum number of straight lines required to make the given figure.
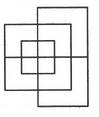
Find the number of triangles in the given figure.
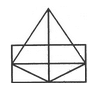
Find the number of triangles in the given figure.
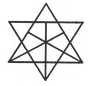
Find the number of triangles in the given figure.
Find the number of triangles in the given figure.
Count the number of triangles and squares in the given figure.
What is the minimum number of different colours required to paint the given figure such that no two adjacent regions have the same colour?
In the adjoining figure, if the centres of all the circles are joined by horizontal and vertical lines, then find the number of squares that can be formed.
Count the number of triangles and squares in the given figure.
Count the number of squares in the given figure.
|
67 videos|50 docs|151 tests
|
|
67 videos|50 docs|151 tests
|




















