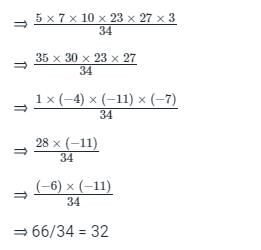Practice Test: Number System- 1 - UPSC MCQ
20 Questions MCQ Test - Practice Test: Number System- 1
Anita had to do a multiplication. Instead of taking 35 as one of the multipliers, she took 53. As a result, the product went up by 540. What is the new product?
A red light flashes three times per minute and a green light flashes five times in 2 min at regular intervals. If both lights start flashing at the same time, how many times do they flash together in each hour?
Let S be the set of prime numbers greater than or equal to 2 and less than 100. Multiply all the elements of S. With how many consecutive zeroes will the product end?
In some code, letters a, b, c, d and e represent numbers 2, 4, 5, 6 and 10. We just do not know which letter represents which number. Consider the following relationships:
I. a + c = e,
II. b – d = d and
III. e + a = b
Which of the following options are true?
The sum of the first 100 natural numbers, 1 to 100 is divisible by:
In a four-digit number, the sum of the first 2 digits is equal to that of the last 2 digits. The sum of the first and last digits is equal to the third digit. Finally, the sum of the second and fourth digits is twice the sum of the other 2 digits. What is the third digit of the number?
All the page numbers from a book are added, beginning at page 1.
However, one page number was added twice by mistake. The sum obtained was 1000. Which page number was added twice?
The integers 34041 and 32506 when divided by a three-digit integer n leave the same remainder. What is n?
What is the least number of soldiers that can be drawn up in troops of 12, 15, 18 and 20 soldiers and also in form of a solid square?
Rohan purchased some pens, pencils and erasers for his young brothers and sisters for the ensuing examinations. He had to buy atleast 11 pieces of each item in a manner that the number of pens purchased is more than the number of pencils, which is more than the number of erasers. He purchased a total of 38 pieces. If the number of pencils cannot be equally divided among his 4 brothers and sisters, how many pens did he purchase?
A nursery has 363, 429 and 693 plants respectively of 3 distinct varieties. It is desired to place these plants in straight rows of plants of 1 variety only so that the number of rows required is the minimum. What is the size of each row and how many rows would be required?
1 ’s are given 100 times, 2 ’s are given 100 times and 3’s are given 100 times. Now numbers are made by arranging these 300 digits in all possible ways. How many of these numbers will be perfect squares?
Find the remainder when 73 * 75 * 78 * 57 * 197 * 37 is divided by 34.
Four bells ring together and ring at an interval of 12 sec, 15 sec, 20 sec, and 30 sec respectively. How many times will they ring together in 8 hours?
After the division of a number successively by 3, 4 and 7, the remainders obtained are 2, 1 and 4 respectively. What will be the remainder if 84 divides the same number?
Teacher said that there were 100 students in his class, 24 of whom were boys and 32 were girls. Which base system did the teacher use in this statement?
If a three digit number ‘abc’ has 2 factors (where a, b, c are digits), how many factors does the 6-digit number ‘abcabc’ have?