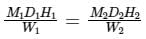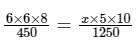Test: Work & Wages - 1 - UPSC MCQ
10 Questions MCQ Test - Test: Work & Wages - 1
Raman can do a work in 5 days, Jatin can do the same work in 7 days and Sachin can do the same work in 9 days. If they do the same work together and they are paid Rs. 2860, then what is the share of Raman?
A can do a work in 5 days while B can do the same work in 8 days. They worked together to complete the work and earned Rs. 6760. Find A’s share?
A can do a piece of work in 20 days while B can do it in 30 days. They work together for 10 days and the rest of the work is done by C in 5 days. If they get Rs 560 for the whole work, how much money will A get?
In a hostel, there is stock of 6,190.80 kg of wheat for feeding 105 students for 22 days. After 5 days, 14 students joined the hostel. How many days will the balance wheat feed the students, if all students consume the same quantity per day?
In a camp, there is a meal for 120 men or 200 children. If 150 children have taken the meal, how many men will be catered-to with remaining meal?
A and B together can do a work in X days, A and C can do that work in 10 days, and B and C can do that work in 8 days. The ratio of efficiencies B and C is 9:1. If the total wages for that work is 34000 Rs. then find the difference between the amount paid to A and B and also find the value of X.
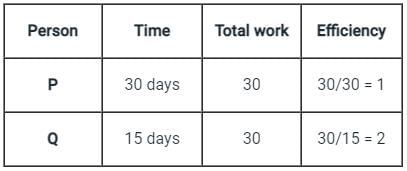
P and Q can complete a piece of work in 30 days and 15 days respectively. They contracted to complete the work for Rs. 60,000. Then find the share of P in the contracted money will be?
A firm reduced employees in the ratio 12 ∶ 5 in time of inflation, and the average wage per employee increased in the ratio 9 ∶ 17. By doing so, the firm saved Rs.46,000. What was the initial expenditure (in Rs) of the firm?
If the operating cost of 6 burners for 6 hours in 8 days is Rs. 450 then find the number of burners if used for 5 hours for 10 day with operating cost of Rs.1250.
A certain number of workers agree to finish a work in 30 days. 10 workers do not come to work, the rest finished the work in 50 days. Find the number of workers who originally agreed to work.