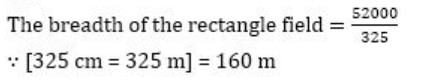Test: Mensuration- 3 - UPSC MCQ
15 Questions MCQ Test CSAT Preparation - Test: Mensuration- 3
There is a right circular cone with base radius 3 units and height 4 units. The surface of this right circular cone is painted. It is then cut into two parts by a plane parallel to the base so that the volume of the top part (the small cone) divided by the volume of the frustum equals the painted area of the top part divided by the painted area of the bottom part. The height of the small cone is
ABCD is a square of side 10 cm. What is the area of the least-sized square that may be inscribed in ABCD with its vertices on the sides of ABCD?
The cost of white washing one m2 is Rs 50. What will be the maximum amount saved in painting the room in the most economical way, if the sum of the length, breadth and height is 21 m and all the sides are integers (floor is not to be white washed)?
A cube is inscribed in a hemisphere of radius R, such that four of its vertices lie on the base of the hemisphere and the other four touch the hemispherical surface of the half-sphere. What is the volume of the cube?
All five faces of a regular pyramid with a square base are found to be of the same area. The height of the pyramid is 3 cm. The total area of all its surfaces (in cm2) is
Under the Indian Posts and Telegraph Act 1885, any package in the form of a right circular cylinder will not be accepted if the sum of its height and the diameter of its base exceeds 10 inches. The height (in inches) of a package of maximum volume that would be accepted is
A cuboid of length 20 m, breadth 15 m and height 12 m is lying on a table. The cuboid is cut into two equal halves by a plane which is perpendicular to the base and passes through a pair of diagonally opposite points of that surface. Then, a second cut is made by a plane which is parallel to the surface of the table again dividing the cuboid into two equal halves. Now this cuboid is divided into four pieces. Out of these four pieces, one piece is now removed from its place. What is the total surface area of the remaining portion of the cuboid?
The area of a rectangular field is 52000 m². This rectangular area has been drawn on a map to the scale 1 cm to 100 m. The length is shown as 3.25 cm on the map. The breadth of the rectangular field is :
Four spheres each of radius 10 cm lie on a horizontal table so that the centres of the spheres form a square of side 20 cm. A fifth sphere also of radius 10 cm is placed on them so that it touches each of these spheres without disturbing them. How many cm above the table is the centre of the fifth sphere?
The square of side 1 cm are cut from four comers of a sheet of tin (having length = 1 and breadth = b) in order to form an open box. If the whole sheet of tin was rolled along its length to form a cylinder, then the volume of the cylinder is equal to (343/4) cm3. Find the volume of the box. (1 and b are integers)
John Nash, an avid mathematician, had his room constructed such that the floor of the room was an equilateral triangle in shape instead of the usual rectangular shape. One day he brought home a bird and tied it to one end of a string and then tied the other end of the string to one of the corners of his room. The next day, he untied the other end of the string from the corner of the room and tied it to a point exactly at the center of the floor of the room. Assuming that the dimensions of the room are relatively large compared to the length of the string, find the number of times, by which the maximum possible space in which the bird can fly, increase.
The perimeter of a triangle is 28 cm and the inradius of the triangle is 2.5 cm. What is the area of the triangle?
An order was placed for the supply of a carpet whose breadth was 6 m and length was 1.44 times the breadth. What be the cost of a carpet whose length and breadth are 40% more and 25% more respectively than the first carpet. Given that the ratio of carpet is Rs. 45 per sq m?
|
208 videos|138 docs|138 tests
|