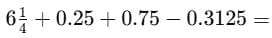Test: Simplification- 2 - CLAT MCQ
21 Questions MCQ Test - Test: Simplification- 2
What should come in the place of question mark (?) in the following equation?
((7 × ?)² / 49) = √81
What approximate value should come in place of the question mark (?) in the given questions?
14.998% of 619.999 =?
Find the value of √(380 + √(380 + √(380 + √(380 + ... ∞))))
The sum of the digits of a two-digit number is 9. If the digits are reversed, the number is decreased by 45. Find the number.
The sum of the digits of a two-digit number is 8. If the digits are reversed, the number is decreased by 54. Find the number.
If the sum of a number and its square is 156, what is the number?
A number when divided by 1092 gives a remainder 60. What remainder would be obtained by dividing the same number by 28?
The sum of squares of two numbers is 85 and the square of first number is 77 more than by the square of second number. The product of the two numbers is
Find the number in the unit place in (321)321 x (325)326.
The approximate value of (4.669 × 4.669 - 2.331 × 2.331) / ((4.669)² + (2.331)² - 4.669 × 4.662) is