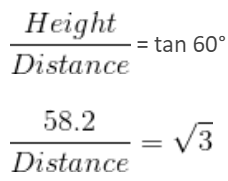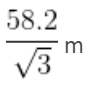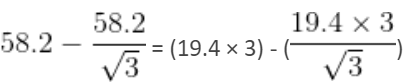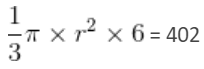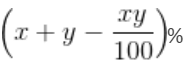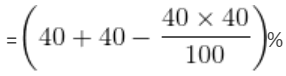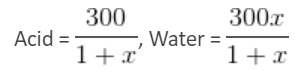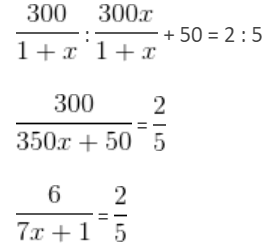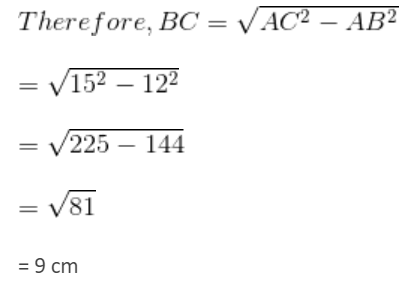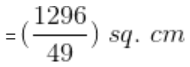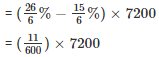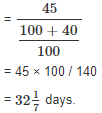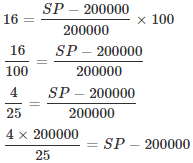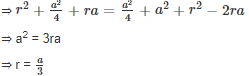SSC CGL (Tier II) Practice Test - 8 - SSC CGL MCQ
30 Questions MCQ Test SSC CGL Tier 1 and Tier 2 Mock Test Series 2026 - SSC CGL (Tier II) Practice Test - 8
The interior angle of a regular polygon exceeds its exterior angle by 108°. The number of sides of the polygon is
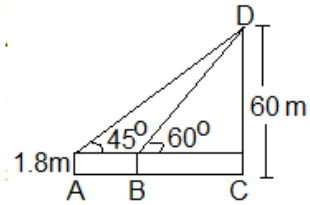
Mohit is standing at some distance from a 60-meter tall building. Mohit is 1.8-metre tall. When Mohit walks towards the building, the angle of elevation from his head becomes 60° from 45°. How much distance (in meters) does Mohit cover towards the building?
In 4 years, at simple interest, the principal increases by 12%. Calculate the amount (in Rs) received at the end of 2 years on Rs 20,000 at the same rate if compounded annually?
Two cards are drawn in succession from a pack of 52 cards. The first card should be a Queen and the second should be a King. What is the probability of doing so if the first card is replaced?
Directions: Study the following line graph to answer the given question:
Sales of Drinks and Food Over the Five Days (Sales in Thousands)
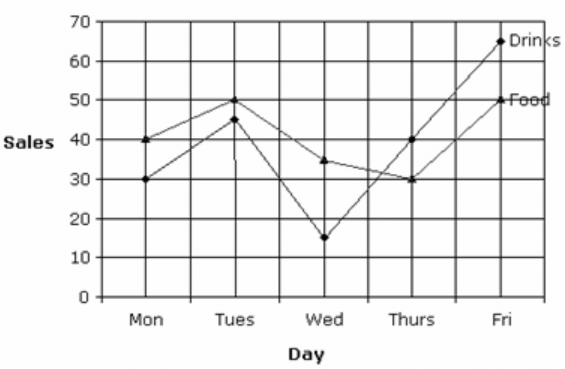
When the sales are modelled mathematically, the growth of sales from Monday to Tuesday is expressed in linear form for both drinks and food. The difference between their growth would be (in thousand)
A person has left an amount of Rs. 1,20,000 to be divided between his two sons, aged 14 years and 12 years such that they get equal amounts when each attains 18 years of age. If the amount gets a simple interest of 5% per annum, the younger son's share at present is
A cylinder with base radius 8 cm and height 2 cm is melted to form a cone of height 6 cm. The radius of the cone will be
Giving two successive discounts of 40% is equal to giving one discount of ________%.
A beaker contains acid and water in the ratio 1 : x, respectively. When 300 ml of the mixture and 50 ml of water are mixed, the ratio of acid to water becomes 2 : 5. What is the value of x?
Directions: Study the following line graph to answer the given question:
Sales of Drinks and Food Over the Five Days (Sales in Thousands)
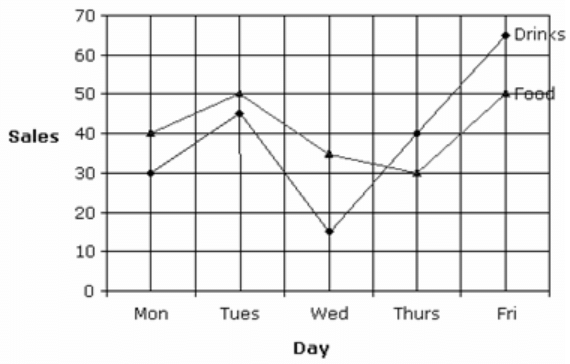
Q. What is the ratio of the differences of the highest sales and the lowest sales of drinks and the food (approx.)?
A man buys two chairs for a total cost of Rs. 900. By selling one for 4/5 of its cost and the other for 5/4 of its cost, he makes a profit of Rs. 90 on the whole transaction. The cost of the lower priced chair is
What is the value of [(sin 59° cos 31° + cos 59° sin 31°) ÷ (cos 20° cos 25° - sin 20° sin 25°)]?
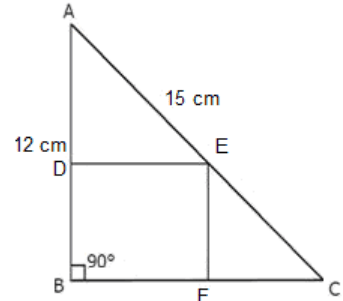
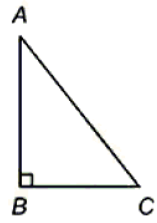
In the given right-angled triangle ABC, AB = 12 cm and AC = 15 cm. A square is inscribed in the triangle. One of the vertices of the square coincides with a vertex of the triangle. What is the maximum possible area (in cm2) of the square?
Directions: Identify the missing number in the series provided.
25, 65, 145, 265, 425, 625, ?
If ![]() and
and 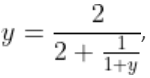 then which of the following can be the value of X + y?
then which of the following can be the value of X + y?
The average of 5 numbers is 4.25. The average of two of them is 4.1, while the average of the other two is 3.62. What is the average of the remaining number?
If the sales tax is reduced from ![]() , then what difference does it make to a person who purchases an article with marked price of Rs. 7200.
, then what difference does it make to a person who purchases an article with marked price of Rs. 7200.
From the following equations x2 + y2 = 41 and x4 - y4 = 369 the value of x and y will be respectively
If the compound interest on a sum for 2 years at ![]() per annum is ₹340, then the simple interest on the same sum at the same rate for the same period of time is
per annum is ₹340, then the simple interest on the same sum at the same rate for the same period of time is
A runs thrice as fast as B and B runs 4 times as fast as C. the distance covered by C in 96 minutes will be covered by A in:
A completed the school project tin 45 days. How many days will B take to complete the same work, if he is 40% more efficient than A?
How many bullets can be made out of a lead cylinder 45 m high and the radius 18 cm, each bullet being 4.5 cm in diameter?
By selling a car for Rs. 2,56,000, Raj gains 28%. If the profit is reduced to 16% then the selling price will be:
The radius of a right circular cylinder is 21 cm and its curved surface area is 5280 cm2. What is its volume?
Perimeter of a triangular field is 540 meter. The ratio of its arms is 5 : 12 : 13. The area of this field is
A man observes a train passing over a bridge 1 km long. The length of the train is half that of bridge. If train clears the bridge in 2 minutes, find the speed of the train.
A company has four departments Human Resource, Marketing, Sales and Information Technology.
The expenses of all departments are shown in the table given below (in thousands).
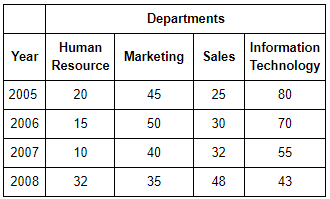
Q. What is the total expenditure of Human Resource, Marketing and Information Technology departments of company?
The following pie-chart and table represent the percentage-wise distribution of number Laptops, say brand A and brand B sold by six shops during six months July – December in the year 2020.
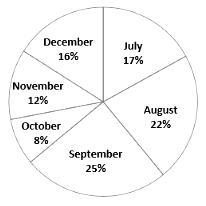
Total number of Laptops sold : 2400
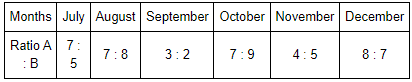
Q. If 25% of the laptops sold by brand B during the month September were sold at a discount, then how many Laptops of brand B were sold without a discount during the month September?
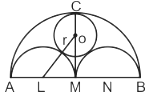
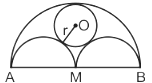
AB is a line segment of length 2a, with M as mid-point. Semicircles are drawn on one side with AM, MB and AB as diameter as shown in the above figure. A circle with centre O and radius r is drawn such that this circle touches all the three semicircles. The value of r is
Select the correct option that indicates the arrangement of the given words in the order in which they appear in an English dictionary.
1. Impersonal
2. Impertinent
3. Impersonate
4. Impermanent
5. Imperturbable
6. Impertinence
7. Imperfection
|
325 docs|152 tests
|