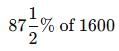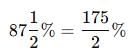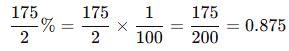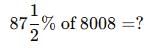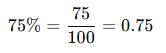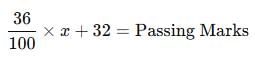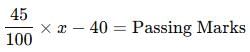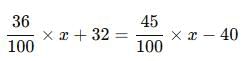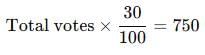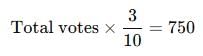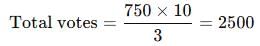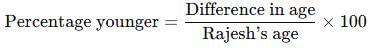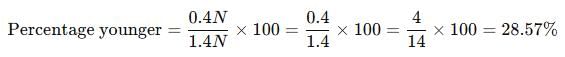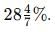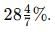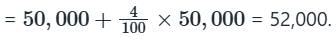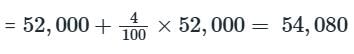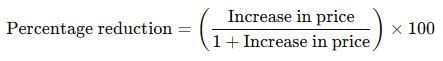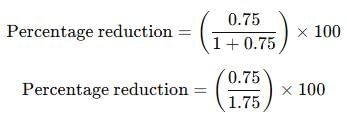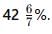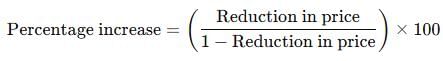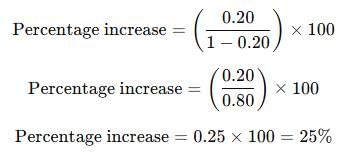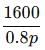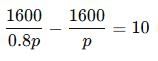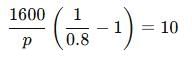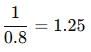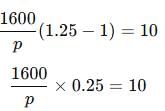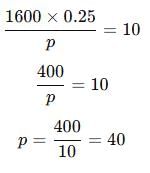Test: Percentage- 2 - CLAT MCQ
20 Questions MCQ Test - Test: Percentage- 2
A student has to secure 35% marks to pass. He gets 650 marks and fails by 50 marks. Find the maximum marks.
A student has to secure 35% marks to pass. He gets 650 marks and fails by 50 marks. Find the maximum marks.
A student who gets 36% of marks, fails by 32 marks. Another candidate who gets 45% marks gets 40 marks more than are necessary for passing. Find the maximum marks.
At an election a candidate secures 40% votes and is defeated by the other candidate by a majority of 2020 votes. Find the total number of votes polled.
At an election a candidate who secured 40% votes and is defeated by the other candidate by a margin of 300 votes. Find the total number of votes recorded.
In an election a candidate got 35% of votes but was defeated by other candidate by 750 votes. Find the total number of votes polled.
Rajesh is 40% older than Neeraj. Find how much % is Neeraj younger than Rajesh.
The population of a town increases at a rate of 4% per annum. At present it is 37500. What will it be after 2 years.
The population of a town increases every year by 4%. If its present population is 50,000, then after 2 years it will be
The price of milk has risen by 75%. Find by how much percent a house holder must reduce his consumption so as not to increase his expenditure.
Price of sugar has increased by 60%. How much % a house holder must reduce his consumption of sugar so as not to increase the expenditure?
Petrol prices are reduced by 20%. Find by how much percent a vehicle owner must increase his consumption of petrol so as not to decrease his expenditure of petrol.
A reduction of 20% in the price of rice enables a man to buy 10 kg more rice for Rs. 1600. Find the reduced price of rice per kg.
A reduction of 20% in the price of apples enables Sumeer to purchase 16 apples more for Rs. 320. Find the reduced price of 10 apples.
A reduction of 20% in the price of rice enables a person to purchase 10 kg more in Rs.600. Find the price of rice per kg before and after reduction of price.