Class 11 Exam > Class 11 Questions > The equation of state of a real gas is p(v-b)...
Start Learning for Free
The equation of state of a real gas is p(v-b) =RT Can the gas be liquefied? Explain?
Most Upvoted Answer
The equation of state of a real gas is p(v-b) =RT Can the gas be lique...
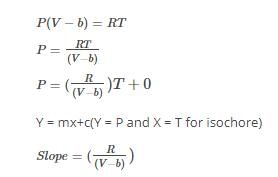
Community Answer
The equation of state of a real gas is p(v-b) =RT Can the gas be lique...
Can the gas be liquefied?
Yes, the gas can be liquefied. The equation of state for a real gas, given as p(v - b) = RT, provides insights into the behavior of the gas and helps determine whether it can be liquefied.
Explanation:
Equation of State:
The equation of state for a gas relates its pressure (p), volume (v), temperature (T), and a constant (R) known as the gas constant. For real gases, this equation is modified to account for the intermolecular forces and the finite size of gas particles.
Liquefaction of Gases:
Liquefaction of a gas refers to the process of converting a gas into its liquid state. This can be achieved by decreasing the temperature and/or increasing the pressure. The behavior of a gas under different conditions is described by its equation of state.
Van der Waals Equation:
The Van der Waals equation is a modification of the ideal gas law that accounts for the intermolecular forces and the volume occupied by gas particles. It is given as:
(p + a/v^2)(v - b) = RT
Where 'a' represents the attractive forces between gas particles and 'b' represents the volume occupied by gas particles.
Effect of 'b' in the Equation:
The term 'b' in the equation of state represents the volume occupied by gas particles. It accounts for the finite size of gas molecules. If the value of 'b' is significant, it implies that the gas particles occupy a considerable volume, making it more difficult to compress the gas and liquefy it.
Conclusion:
In the given equation of state, p(v - b) = RT, the presence of 'b' indicates that the volume occupied by gas particles is being considered. If 'b' is a significant value for a particular gas, it suggests that the gas particles occupy a substantial volume, making it more challenging to liquefy the gas.
Therefore, whether a gas can be liquefied or not depends on the magnitude of 'b' in the equation of state. If 'b' is relatively small, indicating that the gas particles occupy a negligible volume, the gas is more likely to be easily liquefied. However, if 'b' is significant, suggesting that the gas particles occupy a substantial volume, liquefying the gas would require higher pressures and/or lower temperatures.
Yes, the gas can be liquefied. The equation of state for a real gas, given as p(v - b) = RT, provides insights into the behavior of the gas and helps determine whether it can be liquefied.
Explanation:
Equation of State:
The equation of state for a gas relates its pressure (p), volume (v), temperature (T), and a constant (R) known as the gas constant. For real gases, this equation is modified to account for the intermolecular forces and the finite size of gas particles.
Liquefaction of Gases:
Liquefaction of a gas refers to the process of converting a gas into its liquid state. This can be achieved by decreasing the temperature and/or increasing the pressure. The behavior of a gas under different conditions is described by its equation of state.
Van der Waals Equation:
The Van der Waals equation is a modification of the ideal gas law that accounts for the intermolecular forces and the volume occupied by gas particles. It is given as:
(p + a/v^2)(v - b) = RT
Where 'a' represents the attractive forces between gas particles and 'b' represents the volume occupied by gas particles.
Effect of 'b' in the Equation:
The term 'b' in the equation of state represents the volume occupied by gas particles. It accounts for the finite size of gas molecules. If the value of 'b' is significant, it implies that the gas particles occupy a considerable volume, making it more difficult to compress the gas and liquefy it.
Conclusion:
In the given equation of state, p(v - b) = RT, the presence of 'b' indicates that the volume occupied by gas particles is being considered. If 'b' is a significant value for a particular gas, it suggests that the gas particles occupy a substantial volume, making it more challenging to liquefy the gas.
Therefore, whether a gas can be liquefied or not depends on the magnitude of 'b' in the equation of state. If 'b' is relatively small, indicating that the gas particles occupy a negligible volume, the gas is more likely to be easily liquefied. However, if 'b' is significant, suggesting that the gas particles occupy a substantial volume, liquefying the gas would require higher pressures and/or lower temperatures.

|
Explore Courses for Class 11 exam
|

|
Similar Class 11 Doubts
The equation of state of a real gas is p(v-b) =RT Can the gas be liquefied? Explain?
Question Description
The equation of state of a real gas is p(v-b) =RT Can the gas be liquefied? Explain? for Class 11 2025 is part of Class 11 preparation. The Question and answers have been prepared according to the Class 11 exam syllabus. Information about The equation of state of a real gas is p(v-b) =RT Can the gas be liquefied? Explain? covers all topics & solutions for Class 11 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The equation of state of a real gas is p(v-b) =RT Can the gas be liquefied? Explain?.
The equation of state of a real gas is p(v-b) =RT Can the gas be liquefied? Explain? for Class 11 2025 is part of Class 11 preparation. The Question and answers have been prepared according to the Class 11 exam syllabus. Information about The equation of state of a real gas is p(v-b) =RT Can the gas be liquefied? Explain? covers all topics & solutions for Class 11 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The equation of state of a real gas is p(v-b) =RT Can the gas be liquefied? Explain?.
Solutions for The equation of state of a real gas is p(v-b) =RT Can the gas be liquefied? Explain? in English & in Hindi are available as part of our courses for Class 11.
Download more important topics, notes, lectures and mock test series for Class 11 Exam by signing up for free.
Here you can find the meaning of The equation of state of a real gas is p(v-b) =RT Can the gas be liquefied? Explain? defined & explained in the simplest way possible. Besides giving the explanation of
The equation of state of a real gas is p(v-b) =RT Can the gas be liquefied? Explain?, a detailed solution for The equation of state of a real gas is p(v-b) =RT Can the gas be liquefied? Explain? has been provided alongside types of The equation of state of a real gas is p(v-b) =RT Can the gas be liquefied? Explain? theory, EduRev gives you an
ample number of questions to practice The equation of state of a real gas is p(v-b) =RT Can the gas be liquefied? Explain? tests, examples and also practice Class 11 tests.

|
Explore Courses for Class 11 exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.





















