Engineering Mathematics Exam > Engineering Mathematics Questions > State and prove Taylor's theorem on the expan...
Start Learning for Free
State and prove Taylor's theorem on the expansion of f(X h)?
Verified Answer
State and prove Taylor's theorem on the expansion of f(X h)?
According to this Wikipedia article, the expansion for f(x+-h) is:
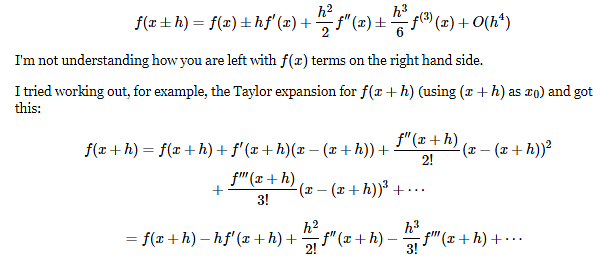
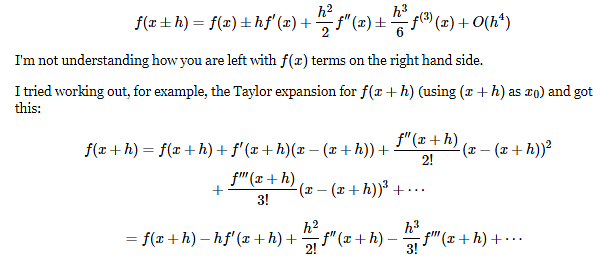
 This question is part of UPSC exam. View all Engineering Mathematics courses
This question is part of UPSC exam. View all Engineering Mathematics courses
Most Upvoted Answer
State and prove Taylor's theorem on the expansion of f(X h)?
Taylor's theorem is a mathematical result that allows us to approximate a function using a polynomial expansion. It states that any sufficiently smooth function can be approximated by a polynomial that is centered around a specific point. This theorem is particularly useful in calculus and numerical analysis.
Taylor's Theorem:
Let f(x) be a function that is infinitely differentiable in an interval I surrounding a point a. Then, for any positive integer n, the function f(x) can be approximated by the nth degree Taylor polynomial:
f(x) ≈ Pn(x) = f(a) + f'(a)(x-a) + f''(a)(x-a)²/2! + ... + fⁿ⁽ⁿ⁾(a)(x-a)ⁿ/ⁿ!
Proof:
To prove Taylor's theorem, we start by considering the function f(x) and its derivatives evaluated at the point a. Let's denote the derivatives as f'(a), f''(a), f'''(a), and so on.
Step 1: Zeroth Degree Taylor Polynomial
The zeroth degree Taylor polynomial is simply the function value at a:
P₀(x) = f(a)
Step 2: First Degree Taylor Polynomial
The first degree Taylor polynomial includes the linear term of the function:
P₁(x) = f(a) + f'(a)(x-a)
Step 3: Second Degree Taylor Polynomial
The second degree Taylor polynomial includes the quadratic term of the function:
P₂(x) = f(a) + f'(a)(x-a) + f''(a)(x-a)²/2!
Step k: kth Degree Taylor Polynomial
Following the same pattern, we can derive the kth degree Taylor polynomial:
Pₖ(x) = f(a) + f'(a)(x-a) + f''(a)(x-a)²/2! + ... + fᵏ(a)(x-a)ᵏ/ᵏ!
Step n: nth Degree Taylor Polynomial
Finally, when we reach the nth degree Taylor polynomial, we have:
Pₙ(x) = f(a) + f'(a)(x-a) + f''(a)(x-a)²/2! + ... + fⁿ⁽ⁿ⁾(a)(x-a)ⁿ/ⁿ!
Approximation:
The nth degree Taylor polynomial becomes an increasingly accurate approximation of the original function f(x) as n approaches infinity. This is because the additional terms in the polynomial capture the behavior of the higher-order derivatives of f(x) at point a.
By using Taylor's theorem, we can approximate the value of a function at a specific point without needing to evaluate the function directly. This is especially useful when dealing with complex functions or when numerical methods are required.
Note: Taylor's theorem also provides a remainder term, known as the Taylor remainder, which quantifies the error between the original function f(x) and its nth degree Taylor polynomial approximation. However, the proof of the remainder term involves more advanced mathematical concepts such as the concept of a limit.
Taylor's Theorem:
Let f(x) be a function that is infinitely differentiable in an interval I surrounding a point a. Then, for any positive integer n, the function f(x) can be approximated by the nth degree Taylor polynomial:
f(x) ≈ Pn(x) = f(a) + f'(a)(x-a) + f''(a)(x-a)²/2! + ... + fⁿ⁽ⁿ⁾(a)(x-a)ⁿ/ⁿ!
Proof:
To prove Taylor's theorem, we start by considering the function f(x) and its derivatives evaluated at the point a. Let's denote the derivatives as f'(a), f''(a), f'''(a), and so on.
Step 1: Zeroth Degree Taylor Polynomial
The zeroth degree Taylor polynomial is simply the function value at a:
P₀(x) = f(a)
Step 2: First Degree Taylor Polynomial
The first degree Taylor polynomial includes the linear term of the function:
P₁(x) = f(a) + f'(a)(x-a)
Step 3: Second Degree Taylor Polynomial
The second degree Taylor polynomial includes the quadratic term of the function:
P₂(x) = f(a) + f'(a)(x-a) + f''(a)(x-a)²/2!
Step k: kth Degree Taylor Polynomial
Following the same pattern, we can derive the kth degree Taylor polynomial:
Pₖ(x) = f(a) + f'(a)(x-a) + f''(a)(x-a)²/2! + ... + fᵏ(a)(x-a)ᵏ/ᵏ!
Step n: nth Degree Taylor Polynomial
Finally, when we reach the nth degree Taylor polynomial, we have:
Pₙ(x) = f(a) + f'(a)(x-a) + f''(a)(x-a)²/2! + ... + fⁿ⁽ⁿ⁾(a)(x-a)ⁿ/ⁿ!
Approximation:
The nth degree Taylor polynomial becomes an increasingly accurate approximation of the original function f(x) as n approaches infinity. This is because the additional terms in the polynomial capture the behavior of the higher-order derivatives of f(x) at point a.
By using Taylor's theorem, we can approximate the value of a function at a specific point without needing to evaluate the function directly. This is especially useful when dealing with complex functions or when numerical methods are required.
Note: Taylor's theorem also provides a remainder term, known as the Taylor remainder, which quantifies the error between the original function f(x) and its nth degree Taylor polynomial approximation. However, the proof of the remainder term involves more advanced mathematical concepts such as the concept of a limit.

|
Explore Courses for Engineering Mathematics exam
|

|
Similar Engineering Mathematics Doubts
State and prove Taylor's theorem on the expansion of f(X h)?
Question Description
State and prove Taylor's theorem on the expansion of f(X h)? for Engineering Mathematics 2024 is part of Engineering Mathematics preparation. The Question and answers have been prepared according to the Engineering Mathematics exam syllabus. Information about State and prove Taylor's theorem on the expansion of f(X h)? covers all topics & solutions for Engineering Mathematics 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for State and prove Taylor's theorem on the expansion of f(X h)?.
State and prove Taylor's theorem on the expansion of f(X h)? for Engineering Mathematics 2024 is part of Engineering Mathematics preparation. The Question and answers have been prepared according to the Engineering Mathematics exam syllabus. Information about State and prove Taylor's theorem on the expansion of f(X h)? covers all topics & solutions for Engineering Mathematics 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for State and prove Taylor's theorem on the expansion of f(X h)?.
Solutions for State and prove Taylor's theorem on the expansion of f(X h)? in English & in Hindi are available as part of our courses for Engineering Mathematics .
Download more important topics, notes, lectures and mock test series for Engineering Mathematics Exam by signing up for free.
Here you can find the meaning of State and prove Taylor's theorem on the expansion of f(X h)? defined & explained in the simplest way possible. Besides giving the explanation of
State and prove Taylor's theorem on the expansion of f(X h)?, a detailed solution for State and prove Taylor's theorem on the expansion of f(X h)? has been provided alongside types of State and prove Taylor's theorem on the expansion of f(X h)? theory, EduRev gives you an
ample number of questions to practice State and prove Taylor's theorem on the expansion of f(X h)? tests, examples and also practice Engineering Mathematics tests.

|
Explore Courses for Engineering Mathematics exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.



















