Class 12 Exam > Class 12 Questions > 64 water drops having equal charges combine t...
Start Learning for Free
64 water drops having equal charges combine to form one bigger drop. The capacitance of the bigger drop, as compared to that of smaller drop will be
- a)64 times
- b)8 times
- c)16 times
- d)4 times
Correct answer is option 'D'. Can you explain this answer?
Verified Answer
64 water drops having equal charges combine to form one bigger drop. T...
Capacitance of the small drop of radius r C8 = 4πε0r and that of the big drop of radius R is CB = 4πε0R .
The volume of 64 small drops,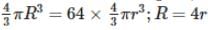
The ratio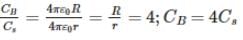
The volume of 64 small drops,
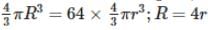
The ratio
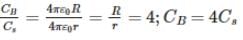
Most Upvoted Answer
64 water drops having equal charges combine to form one bigger drop. T...
When 64 drops will combine to form a bigger drop then the volume will be same in both cases ...
⇒64 × (4/3)πr³ = (4/3)πR³
⇒R = 4r
now, C = 4π∈₀r
⇒ C' = 4π∈₀R = 4π∈₀(4r) = 4C....
Hence, capacitance of bigger drop is 4 times the 64 small drops..
⇒64 × (4/3)πr³ = (4/3)πR³
⇒R = 4r
now, C = 4π∈₀r
⇒ C' = 4π∈₀R = 4π∈₀(4r) = 4C....
Hence, capacitance of bigger drop is 4 times the 64 small drops..
Free Test
FREE
| Start Free Test |
Community Answer
64 water drops having equal charges combine to form one bigger drop. T...
Capacitance of a drop depends on its surface area and the distance between its two surfaces. When 64 drops combine to form one bigger drop, the following changes occur:
- Surface area: The surface area of the bigger drop will be 64 times the surface area of each smaller drop, since all the drops have combined to form one. Hence, the surface area of the bigger drop is 64 times more than the smaller drop.
- Distance between surfaces: The distance between the two surfaces of the bigger drop will be less than the distance between the surfaces of the smaller drop. This is because the drops combine to form a more compact structure, and the distance between the surfaces decreases. Hence, the distance between surfaces of the bigger drop is less than the smaller drop.
Using the formula for capacitance of a spherical conductor, C = 4πε₀r, where r is the radius of the sphere and ε₀ is the permittivity of free space, we can calculate the capacitance of the bigger drop and compare it with the capacitance of each smaller drop.
Let r be the radius of each smaller drop. Then, the radius of the bigger drop will be 4r, since 64 drops combine to form one bigger drop. Using the formula, we get:
- Capacitance of each smaller drop: C₁ = 4πε₀r
- Capacitance of the bigger drop: C₂ = 4πε₀(4r)
Dividing C₂ by C₁, we get:
C₂/C₁ = (4πε₀(4r))/(4πε₀r) = 16
Therefore, the capacitance of the bigger drop is 16 times that of each smaller drop. Hence, the correct answer is option D.
- Surface area: The surface area of the bigger drop will be 64 times the surface area of each smaller drop, since all the drops have combined to form one. Hence, the surface area of the bigger drop is 64 times more than the smaller drop.
- Distance between surfaces: The distance between the two surfaces of the bigger drop will be less than the distance between the surfaces of the smaller drop. This is because the drops combine to form a more compact structure, and the distance between the surfaces decreases. Hence, the distance between surfaces of the bigger drop is less than the smaller drop.
Using the formula for capacitance of a spherical conductor, C = 4πε₀r, where r is the radius of the sphere and ε₀ is the permittivity of free space, we can calculate the capacitance of the bigger drop and compare it with the capacitance of each smaller drop.
Let r be the radius of each smaller drop. Then, the radius of the bigger drop will be 4r, since 64 drops combine to form one bigger drop. Using the formula, we get:
- Capacitance of each smaller drop: C₁ = 4πε₀r
- Capacitance of the bigger drop: C₂ = 4πε₀(4r)
Dividing C₂ by C₁, we get:
C₂/C₁ = (4πε₀(4r))/(4πε₀r) = 16
Therefore, the capacitance of the bigger drop is 16 times that of each smaller drop. Hence, the correct answer is option D.

|
Explore Courses for Class 12 exam
|

|
Question Description
64 water drops having equal charges combine to form one bigger drop. The capacitance of the bigger drop, as compared to that of smaller drop will bea)64 timesb)8 timesc)16 timesd)4 timesCorrect answer is option 'D'. Can you explain this answer? for Class 12 2025 is part of Class 12 preparation. The Question and answers have been prepared according to the Class 12 exam syllabus. Information about 64 water drops having equal charges combine to form one bigger drop. The capacitance of the bigger drop, as compared to that of smaller drop will bea)64 timesb)8 timesc)16 timesd)4 timesCorrect answer is option 'D'. Can you explain this answer? covers all topics & solutions for Class 12 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for 64 water drops having equal charges combine to form one bigger drop. The capacitance of the bigger drop, as compared to that of smaller drop will bea)64 timesb)8 timesc)16 timesd)4 timesCorrect answer is option 'D'. Can you explain this answer?.
64 water drops having equal charges combine to form one bigger drop. The capacitance of the bigger drop, as compared to that of smaller drop will bea)64 timesb)8 timesc)16 timesd)4 timesCorrect answer is option 'D'. Can you explain this answer? for Class 12 2025 is part of Class 12 preparation. The Question and answers have been prepared according to the Class 12 exam syllabus. Information about 64 water drops having equal charges combine to form one bigger drop. The capacitance of the bigger drop, as compared to that of smaller drop will bea)64 timesb)8 timesc)16 timesd)4 timesCorrect answer is option 'D'. Can you explain this answer? covers all topics & solutions for Class 12 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for 64 water drops having equal charges combine to form one bigger drop. The capacitance of the bigger drop, as compared to that of smaller drop will bea)64 timesb)8 timesc)16 timesd)4 timesCorrect answer is option 'D'. Can you explain this answer?.
Solutions for 64 water drops having equal charges combine to form one bigger drop. The capacitance of the bigger drop, as compared to that of smaller drop will bea)64 timesb)8 timesc)16 timesd)4 timesCorrect answer is option 'D'. Can you explain this answer? in English & in Hindi are available as part of our courses for Class 12.
Download more important topics, notes, lectures and mock test series for Class 12 Exam by signing up for free.
Here you can find the meaning of 64 water drops having equal charges combine to form one bigger drop. The capacitance of the bigger drop, as compared to that of smaller drop will bea)64 timesb)8 timesc)16 timesd)4 timesCorrect answer is option 'D'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
64 water drops having equal charges combine to form one bigger drop. The capacitance of the bigger drop, as compared to that of smaller drop will bea)64 timesb)8 timesc)16 timesd)4 timesCorrect answer is option 'D'. Can you explain this answer?, a detailed solution for 64 water drops having equal charges combine to form one bigger drop. The capacitance of the bigger drop, as compared to that of smaller drop will bea)64 timesb)8 timesc)16 timesd)4 timesCorrect answer is option 'D'. Can you explain this answer? has been provided alongside types of 64 water drops having equal charges combine to form one bigger drop. The capacitance of the bigger drop, as compared to that of smaller drop will bea)64 timesb)8 timesc)16 timesd)4 timesCorrect answer is option 'D'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice 64 water drops having equal charges combine to form one bigger drop. The capacitance of the bigger drop, as compared to that of smaller drop will bea)64 timesb)8 timesc)16 timesd)4 timesCorrect answer is option 'D'. Can you explain this answer? tests, examples and also practice Class 12 tests.

|
Explore Courses for Class 12 exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















