Computer Science Engineering (CSE) Exam > Computer Science Engineering (CSE) Questions > A dice is rolled180180times, find the probabi...
Start Learning for Free
A dice is rolled 180180 times, find the probability that face 44 will turn up at least 3535 times.(Assume normal distribution). Assume p(0 < z < 1) = 0.3413
- a)0.147
- b)0.158
- c)0.17
- d)0.2
Correct answer is option 'B'. Can you explain this answer?
Verified Answer
A dice is rolled180180times, find the probability that face44will turn...
Given that n = 180
Required Probability is given by 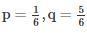
∴ mean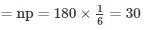
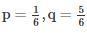
∴ mean
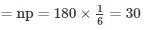
Variance = npq = 25


= 0.5 – 0.3413 = 0.1587
Most Upvoted Answer
A dice is rolled180180times, find the probability that face44will turn...
To solve this problem, we need to use the binomial distribution formula. The binomial distribution formula is given by:
P(X=k) = C(n, k) * p^k * (1-p)^(n-k)
Where:
- n is the number of trials (in this case, the number of times the dice is rolled: 180180)
- k is the number of successful outcomes (in this case, the number of times face 44 turns up: at least 3535)
- p is the probability of a successful outcome (in this case, the probability of face 44 turning up on a single roll)
Since the dice has six faces, each face has an equal probability of turning up, and there are two face 44 on the dice, the probability of face 44 turning up on a single roll is 2/6 = 1/3.
Using the binomial distribution formula, we can calculate the probability of face 44 turning up at least 3535 times:
P(X>=35) = P(X=35) + P(X=36) + ... + P(X=180180)
P(X>=35) = ∑(k=35 to 180180) C(180180, k) * (1/3)^k * (2/3)^(180180-k)
Calculating this sum would require a lot of calculations and would not be feasible manually. To solve this, we can use a normal approximation to the binomial distribution.
For large values of n and when both np and n(1-p) are greater than or equal to 5, the binomial distribution can be approximated by a normal distribution with mean μ = np and standard deviation σ = sqrt(np(1-p)).
In this case, np = 180180 * 1/3 = 60060 and n(1-p) = 180180 * 2/3 = 120120.
We want to find the probability of face 44 turning up at least 3535 times, so k >= 35.
To use the normal approximation, we can transform the inequality:
P(X>=35) = P(X>34) = 1 - P(X< />
Using the normal distribution, we calculate the z-score for k = 34:
z = (k - μ) / σ = (34 - 60060) / sqrt(60060 * (1/3) * (2/3))
We can then use a standard normal distribution table or calculator to find the cumulative probability P(Z<=z) and="" subtract="" it="" from="" 1="" to="" find="" the="" probability="" of="" p(x="">34).
Note: The normal approximation assumes that the conditions for approximation are met, so the result may not be exact but should be a good approximation given the large number of trials.
Unfortunately, without a specific value for k (the number of times face 44 turns up), we cannot provide an exact probability.
P(X=k) = C(n, k) * p^k * (1-p)^(n-k)
Where:
- n is the number of trials (in this case, the number of times the dice is rolled: 180180)
- k is the number of successful outcomes (in this case, the number of times face 44 turns up: at least 3535)
- p is the probability of a successful outcome (in this case, the probability of face 44 turning up on a single roll)
Since the dice has six faces, each face has an equal probability of turning up, and there are two face 44 on the dice, the probability of face 44 turning up on a single roll is 2/6 = 1/3.
Using the binomial distribution formula, we can calculate the probability of face 44 turning up at least 3535 times:
P(X>=35) = P(X=35) + P(X=36) + ... + P(X=180180)
P(X>=35) = ∑(k=35 to 180180) C(180180, k) * (1/3)^k * (2/3)^(180180-k)
Calculating this sum would require a lot of calculations and would not be feasible manually. To solve this, we can use a normal approximation to the binomial distribution.
For large values of n and when both np and n(1-p) are greater than or equal to 5, the binomial distribution can be approximated by a normal distribution with mean μ = np and standard deviation σ = sqrt(np(1-p)).
In this case, np = 180180 * 1/3 = 60060 and n(1-p) = 180180 * 2/3 = 120120.
We want to find the probability of face 44 turning up at least 3535 times, so k >= 35.
To use the normal approximation, we can transform the inequality:
P(X>=35) = P(X>34) = 1 - P(X< />
Using the normal distribution, we calculate the z-score for k = 34:
z = (k - μ) / σ = (34 - 60060) / sqrt(60060 * (1/3) * (2/3))
We can then use a standard normal distribution table or calculator to find the cumulative probability P(Z<=z) and="" subtract="" it="" from="" 1="" to="" find="" the="" probability="" of="" p(x="">34).
Note: The normal approximation assumes that the conditions for approximation are met, so the result may not be exact but should be a good approximation given the large number of trials.
Unfortunately, without a specific value for k (the number of times face 44 turns up), we cannot provide an exact probability.

|
Explore Courses for Computer Science Engineering (CSE) exam
|

|
Question Description
A dice is rolled180180times, find the probability that face44will turn up at least3535times.(Assume normal distribution). Assume p(0 < z < 1) = 0.3413a)0.147b)0.158c)0.17d)0.2Correct answer is option 'B'. Can you explain this answer? for Computer Science Engineering (CSE) 2025 is part of Computer Science Engineering (CSE) preparation. The Question and answers have been prepared according to the Computer Science Engineering (CSE) exam syllabus. Information about A dice is rolled180180times, find the probability that face44will turn up at least3535times.(Assume normal distribution). Assume p(0 < z < 1) = 0.3413a)0.147b)0.158c)0.17d)0.2Correct answer is option 'B'. Can you explain this answer? covers all topics & solutions for Computer Science Engineering (CSE) 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A dice is rolled180180times, find the probability that face44will turn up at least3535times.(Assume normal distribution). Assume p(0 < z < 1) = 0.3413a)0.147b)0.158c)0.17d)0.2Correct answer is option 'B'. Can you explain this answer?.
A dice is rolled180180times, find the probability that face44will turn up at least3535times.(Assume normal distribution). Assume p(0 < z < 1) = 0.3413a)0.147b)0.158c)0.17d)0.2Correct answer is option 'B'. Can you explain this answer? for Computer Science Engineering (CSE) 2025 is part of Computer Science Engineering (CSE) preparation. The Question and answers have been prepared according to the Computer Science Engineering (CSE) exam syllabus. Information about A dice is rolled180180times, find the probability that face44will turn up at least3535times.(Assume normal distribution). Assume p(0 < z < 1) = 0.3413a)0.147b)0.158c)0.17d)0.2Correct answer is option 'B'. Can you explain this answer? covers all topics & solutions for Computer Science Engineering (CSE) 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A dice is rolled180180times, find the probability that face44will turn up at least3535times.(Assume normal distribution). Assume p(0 < z < 1) = 0.3413a)0.147b)0.158c)0.17d)0.2Correct answer is option 'B'. Can you explain this answer?.
Solutions for A dice is rolled180180times, find the probability that face44will turn up at least3535times.(Assume normal distribution). Assume p(0 < z < 1) = 0.3413a)0.147b)0.158c)0.17d)0.2Correct answer is option 'B'. Can you explain this answer? in English & in Hindi are available as part of our courses for Computer Science Engineering (CSE).
Download more important topics, notes, lectures and mock test series for Computer Science Engineering (CSE) Exam by signing up for free.
Here you can find the meaning of A dice is rolled180180times, find the probability that face44will turn up at least3535times.(Assume normal distribution). Assume p(0 < z < 1) = 0.3413a)0.147b)0.158c)0.17d)0.2Correct answer is option 'B'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A dice is rolled180180times, find the probability that face44will turn up at least3535times.(Assume normal distribution). Assume p(0 < z < 1) = 0.3413a)0.147b)0.158c)0.17d)0.2Correct answer is option 'B'. Can you explain this answer?, a detailed solution for A dice is rolled180180times, find the probability that face44will turn up at least3535times.(Assume normal distribution). Assume p(0 < z < 1) = 0.3413a)0.147b)0.158c)0.17d)0.2Correct answer is option 'B'. Can you explain this answer? has been provided alongside types of A dice is rolled180180times, find the probability that face44will turn up at least3535times.(Assume normal distribution). Assume p(0 < z < 1) = 0.3413a)0.147b)0.158c)0.17d)0.2Correct answer is option 'B'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A dice is rolled180180times, find the probability that face44will turn up at least3535times.(Assume normal distribution). Assume p(0 < z < 1) = 0.3413a)0.147b)0.158c)0.17d)0.2Correct answer is option 'B'. Can you explain this answer? tests, examples and also practice Computer Science Engineering (CSE) tests.

|
Explore Courses for Computer Science Engineering (CSE) exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















