Electrical Engineering (EE) Exam > Electrical Engineering (EE) Questions > The coil of a moving coil voltmeter is 50 mm ...
Start Learning for Free
The coil of a moving coil voltmeter is 50 mm long and 40 mm wide and has 120 turns on it. The control spring exerts a torque 200 × 10-6 n – m when the deflection is 100 divisions on full scale. If the flux density of the magnetic field in the air gap is 1.2 wb/m2. The resistance that must be put in series with the coil to give one volt per division.
- a)72 kΩ
- b)36 kΩ
- c)144 kΩ
- d)108 kΩ
Correct answer is option 'C'. Can you explain this answer?
Verified Answer
The coil of a moving coil voltmeter is 50 mm long and 40 mm wide and h...
Tc = 200 × 10-6 N – m
Td = B I N A
= 1.2 × I × 120 × 50 × 40 × 10-6
= 288 × 10-3 I n – m
At equilibrium,
Tc = Td
⇒ 200 × 10-6 = 288 × 10-3 I
⇒ I = 0.694 mA.
Let the resistance of the voltmeter circuit be R voltage across the instrument = 0.694 × 10-3 R
This produces a deflection of 100 divisions.
Volts per division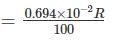
This value should be equal to 1 in order to get 1 volt per division.
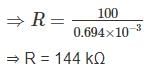
Td = B I N A
= 1.2 × I × 120 × 50 × 40 × 10-6
= 288 × 10-3 I n – m
At equilibrium,
Tc = Td
⇒ 200 × 10-6 = 288 × 10-3 I
⇒ I = 0.694 mA.
Let the resistance of the voltmeter circuit be R voltage across the instrument = 0.694 × 10-3 R
This produces a deflection of 100 divisions.
Volts per division
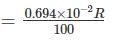
This value should be equal to 1 in order to get 1 volt per division.
Most Upvoted Answer
The coil of a moving coil voltmeter is 50 mm long and 40 mm wide and h...
N/m on the coil when it is deflected through an angle of 50°. Determine the voltage that will cause the coil to be deflected through this angle.
We can use the equation for torque on a coil in a magnetic field:
T = NABIBsinθ
where T is the torque, N is the number of turns on the coil, A is the area of the coil, B is the magnetic field strength, I is the current flowing through the coil, and θ is the angle between the magnetic field and the plane of the coil.
We can rearrange this equation to solve for the current:
I = T/(NABBsinθ)
The voltage V across the coil is related to the current I by Ohm's law:
V = IR
where R is the resistance of the coil. We can assume that the resistance of the coil is constant.
Substituting the values given in the problem, we have:
N = 120 turns
A = 0.05 m x 0.04 m = 0.002 m^2
T = 200 N/m
θ = 50° = 0.87 radians
B = unknown
R = unknown
Solving for B, we have:
B = T/(NABIsinθ) = 200/(120 x 0.002 x I x sin(0.87)) = 2.24 x 10^-3 I^-1 T
We can measure the current I that flows through the coil when it is deflected through the angle θ = 50°. The voltage across the coil is then:
V = IR = I(R) = I(unknown)
Substituting for B and solving for I, we have:
I = T/(NABsinθ) = 200/(120 x 0.002 x 2.24 x 10^-3 x sin(0.87)) = 0.834 A
Finally, we can calculate the voltage:
V = IR = 0.834 x R
The value of R is not given in the problem, so we cannot give a numerical answer for the voltage. However, we can see that the voltage is proportional to the current, which is in turn proportional to the torque on the coil. Therefore, increasing the torque on the coil by increasing the magnetic field strength or the number of turns on the coil will increase the deflection of the coil and the voltage measured by the voltmeter.
We can use the equation for torque on a coil in a magnetic field:
T = NABIBsinθ
where T is the torque, N is the number of turns on the coil, A is the area of the coil, B is the magnetic field strength, I is the current flowing through the coil, and θ is the angle between the magnetic field and the plane of the coil.
We can rearrange this equation to solve for the current:
I = T/(NABBsinθ)
The voltage V across the coil is related to the current I by Ohm's law:
V = IR
where R is the resistance of the coil. We can assume that the resistance of the coil is constant.
Substituting the values given in the problem, we have:
N = 120 turns
A = 0.05 m x 0.04 m = 0.002 m^2
T = 200 N/m
θ = 50° = 0.87 radians
B = unknown
R = unknown
Solving for B, we have:
B = T/(NABIsinθ) = 200/(120 x 0.002 x I x sin(0.87)) = 2.24 x 10^-3 I^-1 T
We can measure the current I that flows through the coil when it is deflected through the angle θ = 50°. The voltage across the coil is then:
V = IR = I(R) = I(unknown)
Substituting for B and solving for I, we have:
I = T/(NABsinθ) = 200/(120 x 0.002 x 2.24 x 10^-3 x sin(0.87)) = 0.834 A
Finally, we can calculate the voltage:
V = IR = 0.834 x R
The value of R is not given in the problem, so we cannot give a numerical answer for the voltage. However, we can see that the voltage is proportional to the current, which is in turn proportional to the torque on the coil. Therefore, increasing the torque on the coil by increasing the magnetic field strength or the number of turns on the coil will increase the deflection of the coil and the voltage measured by the voltmeter.

|
Explore Courses for Electrical Engineering (EE) exam
|

|
Similar Electrical Engineering (EE) Doubts
The coil of a moving coil voltmeter is 50 mm long and 40 mm wide and has 120 turns on it. The control spring exerts a torque 200 × 10-6n – m when the deflection is 100 divisions on full scale. If the flux density of the magnetic field in the air gap is 1.2 wb/m2. The resistance that must be put in series with the coil to give one volt per division.a)72 kΩb)36 kΩc)144 kΩd)108 kΩCorrect answer is option 'C'. Can you explain this answer?
Question Description
The coil of a moving coil voltmeter is 50 mm long and 40 mm wide and has 120 turns on it. The control spring exerts a torque 200 × 10-6n – m when the deflection is 100 divisions on full scale. If the flux density of the magnetic field in the air gap is 1.2 wb/m2. The resistance that must be put in series with the coil to give one volt per division.a)72 kΩb)36 kΩc)144 kΩd)108 kΩCorrect answer is option 'C'. Can you explain this answer? for Electrical Engineering (EE) 2025 is part of Electrical Engineering (EE) preparation. The Question and answers have been prepared according to the Electrical Engineering (EE) exam syllabus. Information about The coil of a moving coil voltmeter is 50 mm long and 40 mm wide and has 120 turns on it. The control spring exerts a torque 200 × 10-6n – m when the deflection is 100 divisions on full scale. If the flux density of the magnetic field in the air gap is 1.2 wb/m2. The resistance that must be put in series with the coil to give one volt per division.a)72 kΩb)36 kΩc)144 kΩd)108 kΩCorrect answer is option 'C'. Can you explain this answer? covers all topics & solutions for Electrical Engineering (EE) 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The coil of a moving coil voltmeter is 50 mm long and 40 mm wide and has 120 turns on it. The control spring exerts a torque 200 × 10-6n – m when the deflection is 100 divisions on full scale. If the flux density of the magnetic field in the air gap is 1.2 wb/m2. The resistance that must be put in series with the coil to give one volt per division.a)72 kΩb)36 kΩc)144 kΩd)108 kΩCorrect answer is option 'C'. Can you explain this answer?.
The coil of a moving coil voltmeter is 50 mm long and 40 mm wide and has 120 turns on it. The control spring exerts a torque 200 × 10-6n – m when the deflection is 100 divisions on full scale. If the flux density of the magnetic field in the air gap is 1.2 wb/m2. The resistance that must be put in series with the coil to give one volt per division.a)72 kΩb)36 kΩc)144 kΩd)108 kΩCorrect answer is option 'C'. Can you explain this answer? for Electrical Engineering (EE) 2025 is part of Electrical Engineering (EE) preparation. The Question and answers have been prepared according to the Electrical Engineering (EE) exam syllabus. Information about The coil of a moving coil voltmeter is 50 mm long and 40 mm wide and has 120 turns on it. The control spring exerts a torque 200 × 10-6n – m when the deflection is 100 divisions on full scale. If the flux density of the magnetic field in the air gap is 1.2 wb/m2. The resistance that must be put in series with the coil to give one volt per division.a)72 kΩb)36 kΩc)144 kΩd)108 kΩCorrect answer is option 'C'. Can you explain this answer? covers all topics & solutions for Electrical Engineering (EE) 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The coil of a moving coil voltmeter is 50 mm long and 40 mm wide and has 120 turns on it. The control spring exerts a torque 200 × 10-6n – m when the deflection is 100 divisions on full scale. If the flux density of the magnetic field in the air gap is 1.2 wb/m2. The resistance that must be put in series with the coil to give one volt per division.a)72 kΩb)36 kΩc)144 kΩd)108 kΩCorrect answer is option 'C'. Can you explain this answer?.
Solutions for The coil of a moving coil voltmeter is 50 mm long and 40 mm wide and has 120 turns on it. The control spring exerts a torque 200 × 10-6n – m when the deflection is 100 divisions on full scale. If the flux density of the magnetic field in the air gap is 1.2 wb/m2. The resistance that must be put in series with the coil to give one volt per division.a)72 kΩb)36 kΩc)144 kΩd)108 kΩCorrect answer is option 'C'. Can you explain this answer? in English & in Hindi are available as part of our courses for Electrical Engineering (EE).
Download more important topics, notes, lectures and mock test series for Electrical Engineering (EE) Exam by signing up for free.
Here you can find the meaning of The coil of a moving coil voltmeter is 50 mm long and 40 mm wide and has 120 turns on it. The control spring exerts a torque 200 × 10-6n – m when the deflection is 100 divisions on full scale. If the flux density of the magnetic field in the air gap is 1.2 wb/m2. The resistance that must be put in series with the coil to give one volt per division.a)72 kΩb)36 kΩc)144 kΩd)108 kΩCorrect answer is option 'C'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
The coil of a moving coil voltmeter is 50 mm long and 40 mm wide and has 120 turns on it. The control spring exerts a torque 200 × 10-6n – m when the deflection is 100 divisions on full scale. If the flux density of the magnetic field in the air gap is 1.2 wb/m2. The resistance that must be put in series with the coil to give one volt per division.a)72 kΩb)36 kΩc)144 kΩd)108 kΩCorrect answer is option 'C'. Can you explain this answer?, a detailed solution for The coil of a moving coil voltmeter is 50 mm long and 40 mm wide and has 120 turns on it. The control spring exerts a torque 200 × 10-6n – m when the deflection is 100 divisions on full scale. If the flux density of the magnetic field in the air gap is 1.2 wb/m2. The resistance that must be put in series with the coil to give one volt per division.a)72 kΩb)36 kΩc)144 kΩd)108 kΩCorrect answer is option 'C'. Can you explain this answer? has been provided alongside types of The coil of a moving coil voltmeter is 50 mm long and 40 mm wide and has 120 turns on it. The control spring exerts a torque 200 × 10-6n – m when the deflection is 100 divisions on full scale. If the flux density of the magnetic field in the air gap is 1.2 wb/m2. The resistance that must be put in series with the coil to give one volt per division.a)72 kΩb)36 kΩc)144 kΩd)108 kΩCorrect answer is option 'C'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice The coil of a moving coil voltmeter is 50 mm long and 40 mm wide and has 120 turns on it. The control spring exerts a torque 200 × 10-6n – m when the deflection is 100 divisions on full scale. If the flux density of the magnetic field in the air gap is 1.2 wb/m2. The resistance that must be put in series with the coil to give one volt per division.a)72 kΩb)36 kΩc)144 kΩd)108 kΩCorrect answer is option 'C'. Can you explain this answer? tests, examples and also practice Electrical Engineering (EE) tests.

|
Explore Courses for Electrical Engineering (EE) exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
























