Class 12 Exam > Class 12 Questions > Three resistances P, Q, R each of 2Ω an...
Start Learning for Free
Three resistances P, Q, R each of 2Ω and anunknown resistance S form the four arms of a Wheatstone bridge circuit. When a resistanceof 6Ω is connected in parallel to S the bridgegets balanced. What is the value of S? [2007]
- a)3Ω
- b)6Ω
- c)1Ω
- d)2Ω
Correct answer is option 'A'. Can you explain this answer?
Verified Answer
Three resistances P, Q, R each of 2Ω and anunknown resistance S ...
A balanced wheatstone bridge simply
requires
requires
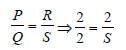
Therefore, S should be 2Ω.
A resistance of 6Ω is connected in parallel.
In parallel combination,
A resistance of 6Ω is connected in parallel.
In parallel combination,
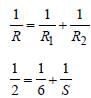
Most Upvoted Answer
Three resistances P, Q, R each of 2Ω and anunknown resistance S ...
There are different ways to approach this problem, but one possible method is to use Ohm's law and the rules for combining resistances in series and parallel. Here's one possible solution:
- First, recall that the resistance of a conductor is defined as the ratio of voltage to current, i.e. R = V/I. In other words, the resistance of a component is directly proportional to the voltage drop across it and inversely proportional to the current flowing through it. This means that if we know the voltage and current in a circuit, we can calculate the resistance of each component.
- Second, note that resistances in series add up, while resistances in parallel combine according to the formula 1/R = 1/R1 + 1/R2 + ... + 1/Rn, where R1, R2, ..., Rn are the individual resistances. In other words, in a series circuit, the total resistance is the sum of the individual resistances, while in a parallel circuit, the reciprocal of the total resistance is the sum of the reciprocals of the individual resistances.
- Now, let's apply these principles to the given problem. We have three resistances P, Q, and R, each of 2 ohms. We want to find the equivalent resistance of the circuit when these three resistances are connected in different ways.
- First, let's consider the case when the resistances are connected in series. This means that the current flows through each resistance in turn, and the voltage is divided among them. Since the resistances are the same, the voltage drop across each one is the same, and we can write Ohm's law as V = IR, where V is the total voltage, I is the current, and R is the total resistance. We also know that the voltage drop across each resistance is 2V/3 (since the total voltage is divided equally among them), so we can write V = 2V/3 + 2V/3 + 2V/3 = 6V/3 = 2V. Therefore, I = V/R = 2V/6 = V/3. Now we can use Ohm's law again to find the individual currents through each resistance: IP = VP/RP = (V/3) / 2 = V/6, IQ = VQ/RQ = (V/3) / 2 = V/6, IR = VR/RR = (V/3) / 2 = V/6. Finally, we can use the formula for resistances in series to find the total resistance: Rseries = RP + RQ + RR = 2 + 2 + 2 = 6 ohms. Therefore, the equivalent resistance of the circuit when the resistances are connected in series is 6 ohms.
- Second, let's consider the case when the resistances are connected in parallel. This means that the current is divided among the resistances, and the voltage drop across each one is the same. Since the resistances are the same, the current through each one is the same, and we can write Ohm's law as I = V/R. We also know that the total current is I = V/2, since the voltage drop across the parallel combination is the same as the total voltage. Therefore, the current through each resistance is I/3 = (V/2)
- First, recall that the resistance of a conductor is defined as the ratio of voltage to current, i.e. R = V/I. In other words, the resistance of a component is directly proportional to the voltage drop across it and inversely proportional to the current flowing through it. This means that if we know the voltage and current in a circuit, we can calculate the resistance of each component.
- Second, note that resistances in series add up, while resistances in parallel combine according to the formula 1/R = 1/R1 + 1/R2 + ... + 1/Rn, where R1, R2, ..., Rn are the individual resistances. In other words, in a series circuit, the total resistance is the sum of the individual resistances, while in a parallel circuit, the reciprocal of the total resistance is the sum of the reciprocals of the individual resistances.
- Now, let's apply these principles to the given problem. We have three resistances P, Q, and R, each of 2 ohms. We want to find the equivalent resistance of the circuit when these three resistances are connected in different ways.
- First, let's consider the case when the resistances are connected in series. This means that the current flows through each resistance in turn, and the voltage is divided among them. Since the resistances are the same, the voltage drop across each one is the same, and we can write Ohm's law as V = IR, where V is the total voltage, I is the current, and R is the total resistance. We also know that the voltage drop across each resistance is 2V/3 (since the total voltage is divided equally among them), so we can write V = 2V/3 + 2V/3 + 2V/3 = 6V/3 = 2V. Therefore, I = V/R = 2V/6 = V/3. Now we can use Ohm's law again to find the individual currents through each resistance: IP = VP/RP = (V/3) / 2 = V/6, IQ = VQ/RQ = (V/3) / 2 = V/6, IR = VR/RR = (V/3) / 2 = V/6. Finally, we can use the formula for resistances in series to find the total resistance: Rseries = RP + RQ + RR = 2 + 2 + 2 = 6 ohms. Therefore, the equivalent resistance of the circuit when the resistances are connected in series is 6 ohms.
- Second, let's consider the case when the resistances are connected in parallel. This means that the current is divided among the resistances, and the voltage drop across each one is the same. Since the resistances are the same, the current through each one is the same, and we can write Ohm's law as I = V/R. We also know that the total current is I = V/2, since the voltage drop across the parallel combination is the same as the total voltage. Therefore, the current through each resistance is I/3 = (V/2)

|
Explore Courses for Class 12 exam
|

|
Similar Class 12 Doubts
Three resistances P, Q, R each of 2Ω and anunknown resistance S form the four arms of a Wheatstone bridge circuit. When a resistanceof 6Ω is connected in parallel to S the bridgegets balanced. What is the value of S?[2007]a)3Ωb)6Ωc)1Ωd)2ΩCorrect answer is option 'A'. Can you explain this answer?
Question Description
Three resistances P, Q, R each of 2Ω and anunknown resistance S form the four arms of a Wheatstone bridge circuit. When a resistanceof 6Ω is connected in parallel to S the bridgegets balanced. What is the value of S?[2007]a)3Ωb)6Ωc)1Ωd)2ΩCorrect answer is option 'A'. Can you explain this answer? for Class 12 2025 is part of Class 12 preparation. The Question and answers have been prepared according to the Class 12 exam syllabus. Information about Three resistances P, Q, R each of 2Ω and anunknown resistance S form the four arms of a Wheatstone bridge circuit. When a resistanceof 6Ω is connected in parallel to S the bridgegets balanced. What is the value of S?[2007]a)3Ωb)6Ωc)1Ωd)2ΩCorrect answer is option 'A'. Can you explain this answer? covers all topics & solutions for Class 12 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Three resistances P, Q, R each of 2Ω and anunknown resistance S form the four arms of a Wheatstone bridge circuit. When a resistanceof 6Ω is connected in parallel to S the bridgegets balanced. What is the value of S?[2007]a)3Ωb)6Ωc)1Ωd)2ΩCorrect answer is option 'A'. Can you explain this answer?.
Three resistances P, Q, R each of 2Ω and anunknown resistance S form the four arms of a Wheatstone bridge circuit. When a resistanceof 6Ω is connected in parallel to S the bridgegets balanced. What is the value of S?[2007]a)3Ωb)6Ωc)1Ωd)2ΩCorrect answer is option 'A'. Can you explain this answer? for Class 12 2025 is part of Class 12 preparation. The Question and answers have been prepared according to the Class 12 exam syllabus. Information about Three resistances P, Q, R each of 2Ω and anunknown resistance S form the four arms of a Wheatstone bridge circuit. When a resistanceof 6Ω is connected in parallel to S the bridgegets balanced. What is the value of S?[2007]a)3Ωb)6Ωc)1Ωd)2ΩCorrect answer is option 'A'. Can you explain this answer? covers all topics & solutions for Class 12 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Three resistances P, Q, R each of 2Ω and anunknown resistance S form the four arms of a Wheatstone bridge circuit. When a resistanceof 6Ω is connected in parallel to S the bridgegets balanced. What is the value of S?[2007]a)3Ωb)6Ωc)1Ωd)2ΩCorrect answer is option 'A'. Can you explain this answer?.
Solutions for Three resistances P, Q, R each of 2Ω and anunknown resistance S form the four arms of a Wheatstone bridge circuit. When a resistanceof 6Ω is connected in parallel to S the bridgegets balanced. What is the value of S?[2007]a)3Ωb)6Ωc)1Ωd)2ΩCorrect answer is option 'A'. Can you explain this answer? in English & in Hindi are available as part of our courses for Class 12.
Download more important topics, notes, lectures and mock test series for Class 12 Exam by signing up for free.
Here you can find the meaning of Three resistances P, Q, R each of 2Ω and anunknown resistance S form the four arms of a Wheatstone bridge circuit. When a resistanceof 6Ω is connected in parallel to S the bridgegets balanced. What is the value of S?[2007]a)3Ωb)6Ωc)1Ωd)2ΩCorrect answer is option 'A'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Three resistances P, Q, R each of 2Ω and anunknown resistance S form the four arms of a Wheatstone bridge circuit. When a resistanceof 6Ω is connected in parallel to S the bridgegets balanced. What is the value of S?[2007]a)3Ωb)6Ωc)1Ωd)2ΩCorrect answer is option 'A'. Can you explain this answer?, a detailed solution for Three resistances P, Q, R each of 2Ω and anunknown resistance S form the four arms of a Wheatstone bridge circuit. When a resistanceof 6Ω is connected in parallel to S the bridgegets balanced. What is the value of S?[2007]a)3Ωb)6Ωc)1Ωd)2ΩCorrect answer is option 'A'. Can you explain this answer? has been provided alongside types of Three resistances P, Q, R each of 2Ω and anunknown resistance S form the four arms of a Wheatstone bridge circuit. When a resistanceof 6Ω is connected in parallel to S the bridgegets balanced. What is the value of S?[2007]a)3Ωb)6Ωc)1Ωd)2ΩCorrect answer is option 'A'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Three resistances P, Q, R each of 2Ω and anunknown resistance S form the four arms of a Wheatstone bridge circuit. When a resistanceof 6Ω is connected in parallel to S the bridgegets balanced. What is the value of S?[2007]a)3Ωb)6Ωc)1Ωd)2ΩCorrect answer is option 'A'. Can you explain this answer? tests, examples and also practice Class 12 tests.

|
Explore Courses for Class 12 exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.



















