Civil Engineering (CE) Exam > Civil Engineering (CE) Questions > A traffic survey is conducted on an intersect...
Start Learning for Free
A traffic survey is conducted on an intersection to compute practical capacity yields the following results:
The width of the weaving section = 12m
Length of the weaving section = 54 m
The proportion of weaving traffic = 60%
The average width of entry and exit = 8m
The practical capacity (in vehicle/hr) of the rotary on the basis of the above data will be
Correct answer is '3660-3770'. Can you explain this answer?
Verified Answer
A traffic survey is conducted on an intersection to compute practical ...
Concept:
Practical capacity of Rotary
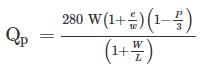
Where W = width of weaving section.
e = Average width at entry and exit = 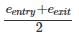
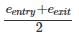
P = proportion of weaving traffic
L = length of the weaving section.
The above expression will be valid only when these four conditions will be satisfied
A. 6m ≤ w ≤ 18m
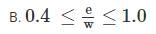
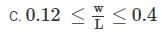
D. 0.4 ≤ P ≤ 1
Calculation:
Given:
W = 15m
L = 54m
e = 8m
P = 60%
Practical capacity of Rotary

Qp = 3665.5 vehicle/hr
Most Upvoted Answer
A traffic survey is conducted on an intersection to compute practical ...
Given Data:
- Width of the weaving section = 12m
- Length of the weaving section = 54m
- Proportion of weaving traffic = 60%
- Average width of entry and exit = 8m
Calculating the Weaving Traffic Volume:
To compute the practical capacity of the intersection, we first need to calculate the weaving traffic volume. We can do this by multiplying the length of the weaving section by the width of the weaving section and the proportion of weaving traffic:
Weaving Traffic Volume = Length of Weaving Section * Width of Weaving Section * Proportion of Weaving Traffic
= 54m * 12m * 0.60
= 388.8 square meters
Calculating the Capacity:
Next, we need to calculate the capacity of the intersection. The capacity represents the maximum number of vehicles that can pass through the intersection per hour. It can be calculated using the formula:
Capacity = (Weaving Traffic Volume / Width of Entry and Exit) * 3600
= (388.8 square meters / 8m) * 3600
= 194400 vehicles/hr
Range of Practical Capacity:
The practical capacity of the intersection can vary depending on various factors such as signal timings, driver behavior, and road conditions. The range of practical capacity is typically given to account for these variations. In this case, the practical capacity is given as 3660-3770 vehicles/hr.
Therefore, the correct answer is '3660-3770' vehicles/hr.
- Width of the weaving section = 12m
- Length of the weaving section = 54m
- Proportion of weaving traffic = 60%
- Average width of entry and exit = 8m
Calculating the Weaving Traffic Volume:
To compute the practical capacity of the intersection, we first need to calculate the weaving traffic volume. We can do this by multiplying the length of the weaving section by the width of the weaving section and the proportion of weaving traffic:
Weaving Traffic Volume = Length of Weaving Section * Width of Weaving Section * Proportion of Weaving Traffic
= 54m * 12m * 0.60
= 388.8 square meters
Calculating the Capacity:
Next, we need to calculate the capacity of the intersection. The capacity represents the maximum number of vehicles that can pass through the intersection per hour. It can be calculated using the formula:
Capacity = (Weaving Traffic Volume / Width of Entry and Exit) * 3600
= (388.8 square meters / 8m) * 3600
= 194400 vehicles/hr
Range of Practical Capacity:
The practical capacity of the intersection can vary depending on various factors such as signal timings, driver behavior, and road conditions. The range of practical capacity is typically given to account for these variations. In this case, the practical capacity is given as 3660-3770 vehicles/hr.
Therefore, the correct answer is '3660-3770' vehicles/hr.

|
Explore Courses for Civil Engineering (CE) exam
|

|
Similar Civil Engineering (CE) Doubts
Question Description
A traffic survey is conducted on an intersection to compute practical capacity yields the following results:The width of the weaving section = 12mLength of the weaving section = 54 mThe proportion of weaving traffic = 60%The average width of entry and exit = 8mThe practical capacity (in vehicle/hr) of the rotary on the basis of the above data will beCorrect answer is '3660-3770'. Can you explain this answer? for Civil Engineering (CE) 2025 is part of Civil Engineering (CE) preparation. The Question and answers have been prepared according to the Civil Engineering (CE) exam syllabus. Information about A traffic survey is conducted on an intersection to compute practical capacity yields the following results:The width of the weaving section = 12mLength of the weaving section = 54 mThe proportion of weaving traffic = 60%The average width of entry and exit = 8mThe practical capacity (in vehicle/hr) of the rotary on the basis of the above data will beCorrect answer is '3660-3770'. Can you explain this answer? covers all topics & solutions for Civil Engineering (CE) 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A traffic survey is conducted on an intersection to compute practical capacity yields the following results:The width of the weaving section = 12mLength of the weaving section = 54 mThe proportion of weaving traffic = 60%The average width of entry and exit = 8mThe practical capacity (in vehicle/hr) of the rotary on the basis of the above data will beCorrect answer is '3660-3770'. Can you explain this answer?.
A traffic survey is conducted on an intersection to compute practical capacity yields the following results:The width of the weaving section = 12mLength of the weaving section = 54 mThe proportion of weaving traffic = 60%The average width of entry and exit = 8mThe practical capacity (in vehicle/hr) of the rotary on the basis of the above data will beCorrect answer is '3660-3770'. Can you explain this answer? for Civil Engineering (CE) 2025 is part of Civil Engineering (CE) preparation. The Question and answers have been prepared according to the Civil Engineering (CE) exam syllabus. Information about A traffic survey is conducted on an intersection to compute practical capacity yields the following results:The width of the weaving section = 12mLength of the weaving section = 54 mThe proportion of weaving traffic = 60%The average width of entry and exit = 8mThe practical capacity (in vehicle/hr) of the rotary on the basis of the above data will beCorrect answer is '3660-3770'. Can you explain this answer? covers all topics & solutions for Civil Engineering (CE) 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A traffic survey is conducted on an intersection to compute practical capacity yields the following results:The width of the weaving section = 12mLength of the weaving section = 54 mThe proportion of weaving traffic = 60%The average width of entry and exit = 8mThe practical capacity (in vehicle/hr) of the rotary on the basis of the above data will beCorrect answer is '3660-3770'. Can you explain this answer?.
Solutions for A traffic survey is conducted on an intersection to compute practical capacity yields the following results:The width of the weaving section = 12mLength of the weaving section = 54 mThe proportion of weaving traffic = 60%The average width of entry and exit = 8mThe practical capacity (in vehicle/hr) of the rotary on the basis of the above data will beCorrect answer is '3660-3770'. Can you explain this answer? in English & in Hindi are available as part of our courses for Civil Engineering (CE).
Download more important topics, notes, lectures and mock test series for Civil Engineering (CE) Exam by signing up for free.
Here you can find the meaning of A traffic survey is conducted on an intersection to compute practical capacity yields the following results:The width of the weaving section = 12mLength of the weaving section = 54 mThe proportion of weaving traffic = 60%The average width of entry and exit = 8mThe practical capacity (in vehicle/hr) of the rotary on the basis of the above data will beCorrect answer is '3660-3770'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A traffic survey is conducted on an intersection to compute practical capacity yields the following results:The width of the weaving section = 12mLength of the weaving section = 54 mThe proportion of weaving traffic = 60%The average width of entry and exit = 8mThe practical capacity (in vehicle/hr) of the rotary on the basis of the above data will beCorrect answer is '3660-3770'. Can you explain this answer?, a detailed solution for A traffic survey is conducted on an intersection to compute practical capacity yields the following results:The width of the weaving section = 12mLength of the weaving section = 54 mThe proportion of weaving traffic = 60%The average width of entry and exit = 8mThe practical capacity (in vehicle/hr) of the rotary on the basis of the above data will beCorrect answer is '3660-3770'. Can you explain this answer? has been provided alongside types of A traffic survey is conducted on an intersection to compute practical capacity yields the following results:The width of the weaving section = 12mLength of the weaving section = 54 mThe proportion of weaving traffic = 60%The average width of entry and exit = 8mThe practical capacity (in vehicle/hr) of the rotary on the basis of the above data will beCorrect answer is '3660-3770'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A traffic survey is conducted on an intersection to compute practical capacity yields the following results:The width of the weaving section = 12mLength of the weaving section = 54 mThe proportion of weaving traffic = 60%The average width of entry and exit = 8mThe practical capacity (in vehicle/hr) of the rotary on the basis of the above data will beCorrect answer is '3660-3770'. Can you explain this answer? tests, examples and also practice Civil Engineering (CE) tests.

|
Explore Courses for Civil Engineering (CE) exam
|

|
Signup to solve all Doubts
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


























