Civil Engineering (CE) Exam > Civil Engineering (CE) Questions > A simply supported rectangular prestressed co...
Start Learning for Free
A simply supported rectangular prestressed concrete beam of span 9 m has to be prestressed with a force of 2000 kN. The profile of the cable is parabolic with zero eccentricity at ends. If the maximum dip (allowable) of the tendon at the mid-span to balance the external load is 0.18 m, the maximum uniformly distributed load (throughout the span) the beam can carry will be _____kN/m. (Neglect the self weight of the beam).
Correct answer is '35-36'. Can you explain this answer?
Verified Answer
A simply supported rectangular prestressed concrete beam of span 9 m h...
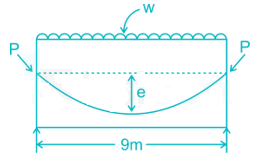
Equating the moments
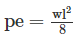
P = Prestressing force = 2000 kN
l = span of the beam = 9 m
w = load on the beam
e = eccentricity of the tendon = 0.18 m
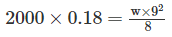
w = 35.55 kN/m
Most Upvoted Answer
A simply supported rectangular prestressed concrete beam of span 9 m h...
Given data:
- Span of the beam = 9 m
- Prestressing force = 2000 kN
- Maximum dip of the tendon at mid-span = 0.18 m
Approach:
To find the maximum uniformly distributed load the beam can carry, we need to determine the maximum bending moment at mid-span. This can be done by considering the equilibrium of forces and moments.
Step 1: Find the cable profile:
- The cable profile is parabolic with zero eccentricity at the ends.
- Since the cable is symmetrical, the maximum dip occurs at the mid-span.
- The maximum dip of the tendon at mid-span is given as 0.18 m.
Step 2: Determine the force in the cable at mid-span:
- The force in the cable at mid-span can be calculated using the equation for a parabolic cable profile.
- The equation for a parabolic cable profile is given as:
y = (L/2)^2 / (8a)
where y = dip of the tendon at a distance x from one end of the beam,
L = span of the beam,
a = constant (to be determined)
- Substituting the given values, we have:
0.18 = (9/2)^2 / (8a)
Solving for a, we get a = 0.5625
- Now, substituting this value of a into the equation for the cable profile, we can determine the force in the cable at mid-span:
y = (9/2)^2 / (8*0.5625)
y = 0.5625 kN
Step 3: Determine the external load at mid-span:
- Since the beam is simply supported, the external load at mid-span will be half of the total load.
- The total load is the sum of the prestressing force and the external load.
- Therefore, the external load at mid-span is given as:
External load = (2000 + 2*y) kN
Step 4: Determine the maximum bending moment at mid-span:
- The maximum bending moment at mid-span occurs when the external load is maximum.
- The maximum bending moment can be calculated using the equation:
M = (wL^2) / 8
where M = maximum bending moment at mid-span,
w = uniformly distributed load (to be determined),
L = span of the beam
- Substituting the given values, we have:
(2000 + 2*y) = (w*9^2) / 8
Solving for w, we get w = 35.15625 kN/m
Answer:
The maximum uniformly distributed load the beam can carry is approximately 35-36 kN/m.
- Span of the beam = 9 m
- Prestressing force = 2000 kN
- Maximum dip of the tendon at mid-span = 0.18 m
Approach:
To find the maximum uniformly distributed load the beam can carry, we need to determine the maximum bending moment at mid-span. This can be done by considering the equilibrium of forces and moments.
Step 1: Find the cable profile:
- The cable profile is parabolic with zero eccentricity at the ends.
- Since the cable is symmetrical, the maximum dip occurs at the mid-span.
- The maximum dip of the tendon at mid-span is given as 0.18 m.
Step 2: Determine the force in the cable at mid-span:
- The force in the cable at mid-span can be calculated using the equation for a parabolic cable profile.
- The equation for a parabolic cable profile is given as:
y = (L/2)^2 / (8a)
where y = dip of the tendon at a distance x from one end of the beam,
L = span of the beam,
a = constant (to be determined)
- Substituting the given values, we have:
0.18 = (9/2)^2 / (8a)
Solving for a, we get a = 0.5625
- Now, substituting this value of a into the equation for the cable profile, we can determine the force in the cable at mid-span:
y = (9/2)^2 / (8*0.5625)
y = 0.5625 kN
Step 3: Determine the external load at mid-span:
- Since the beam is simply supported, the external load at mid-span will be half of the total load.
- The total load is the sum of the prestressing force and the external load.
- Therefore, the external load at mid-span is given as:
External load = (2000 + 2*y) kN
Step 4: Determine the maximum bending moment at mid-span:
- The maximum bending moment at mid-span occurs when the external load is maximum.
- The maximum bending moment can be calculated using the equation:
M = (wL^2) / 8
where M = maximum bending moment at mid-span,
w = uniformly distributed load (to be determined),
L = span of the beam
- Substituting the given values, we have:
(2000 + 2*y) = (w*9^2) / 8
Solving for w, we get w = 35.15625 kN/m
Answer:
The maximum uniformly distributed load the beam can carry is approximately 35-36 kN/m.

|
Explore Courses for Civil Engineering (CE) exam
|

|
Similar Civil Engineering (CE) Doubts
A simply supported rectangular prestressed concrete beam of span 9 m has to be prestressed with a force of 2000 kN. The profile of the cable is parabolic with zero eccentricity at ends. If the maximum dip (allowable) of the tendon at the mid-span to balance the external load is 0.18 m, the maximum uniformly distributed load (throughout the span) the beam can carry will be _____kN/m. (Neglect the self weight of the beam).Correct answer is '35-36'. Can you explain this answer?
Question Description
A simply supported rectangular prestressed concrete beam of span 9 m has to be prestressed with a force of 2000 kN. The profile of the cable is parabolic with zero eccentricity at ends. If the maximum dip (allowable) of the tendon at the mid-span to balance the external load is 0.18 m, the maximum uniformly distributed load (throughout the span) the beam can carry will be _____kN/m. (Neglect the self weight of the beam).Correct answer is '35-36'. Can you explain this answer? for Civil Engineering (CE) 2025 is part of Civil Engineering (CE) preparation. The Question and answers have been prepared according to the Civil Engineering (CE) exam syllabus. Information about A simply supported rectangular prestressed concrete beam of span 9 m has to be prestressed with a force of 2000 kN. The profile of the cable is parabolic with zero eccentricity at ends. If the maximum dip (allowable) of the tendon at the mid-span to balance the external load is 0.18 m, the maximum uniformly distributed load (throughout the span) the beam can carry will be _____kN/m. (Neglect the self weight of the beam).Correct answer is '35-36'. Can you explain this answer? covers all topics & solutions for Civil Engineering (CE) 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A simply supported rectangular prestressed concrete beam of span 9 m has to be prestressed with a force of 2000 kN. The profile of the cable is parabolic with zero eccentricity at ends. If the maximum dip (allowable) of the tendon at the mid-span to balance the external load is 0.18 m, the maximum uniformly distributed load (throughout the span) the beam can carry will be _____kN/m. (Neglect the self weight of the beam).Correct answer is '35-36'. Can you explain this answer?.
A simply supported rectangular prestressed concrete beam of span 9 m has to be prestressed with a force of 2000 kN. The profile of the cable is parabolic with zero eccentricity at ends. If the maximum dip (allowable) of the tendon at the mid-span to balance the external load is 0.18 m, the maximum uniformly distributed load (throughout the span) the beam can carry will be _____kN/m. (Neglect the self weight of the beam).Correct answer is '35-36'. Can you explain this answer? for Civil Engineering (CE) 2025 is part of Civil Engineering (CE) preparation. The Question and answers have been prepared according to the Civil Engineering (CE) exam syllabus. Information about A simply supported rectangular prestressed concrete beam of span 9 m has to be prestressed with a force of 2000 kN. The profile of the cable is parabolic with zero eccentricity at ends. If the maximum dip (allowable) of the tendon at the mid-span to balance the external load is 0.18 m, the maximum uniformly distributed load (throughout the span) the beam can carry will be _____kN/m. (Neglect the self weight of the beam).Correct answer is '35-36'. Can you explain this answer? covers all topics & solutions for Civil Engineering (CE) 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A simply supported rectangular prestressed concrete beam of span 9 m has to be prestressed with a force of 2000 kN. The profile of the cable is parabolic with zero eccentricity at ends. If the maximum dip (allowable) of the tendon at the mid-span to balance the external load is 0.18 m, the maximum uniformly distributed load (throughout the span) the beam can carry will be _____kN/m. (Neglect the self weight of the beam).Correct answer is '35-36'. Can you explain this answer?.
Solutions for A simply supported rectangular prestressed concrete beam of span 9 m has to be prestressed with a force of 2000 kN. The profile of the cable is parabolic with zero eccentricity at ends. If the maximum dip (allowable) of the tendon at the mid-span to balance the external load is 0.18 m, the maximum uniformly distributed load (throughout the span) the beam can carry will be _____kN/m. (Neglect the self weight of the beam).Correct answer is '35-36'. Can you explain this answer? in English & in Hindi are available as part of our courses for Civil Engineering (CE).
Download more important topics, notes, lectures and mock test series for Civil Engineering (CE) Exam by signing up for free.
Here you can find the meaning of A simply supported rectangular prestressed concrete beam of span 9 m has to be prestressed with a force of 2000 kN. The profile of the cable is parabolic with zero eccentricity at ends. If the maximum dip (allowable) of the tendon at the mid-span to balance the external load is 0.18 m, the maximum uniformly distributed load (throughout the span) the beam can carry will be _____kN/m. (Neglect the self weight of the beam).Correct answer is '35-36'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A simply supported rectangular prestressed concrete beam of span 9 m has to be prestressed with a force of 2000 kN. The profile of the cable is parabolic with zero eccentricity at ends. If the maximum dip (allowable) of the tendon at the mid-span to balance the external load is 0.18 m, the maximum uniformly distributed load (throughout the span) the beam can carry will be _____kN/m. (Neglect the self weight of the beam).Correct answer is '35-36'. Can you explain this answer?, a detailed solution for A simply supported rectangular prestressed concrete beam of span 9 m has to be prestressed with a force of 2000 kN. The profile of the cable is parabolic with zero eccentricity at ends. If the maximum dip (allowable) of the tendon at the mid-span to balance the external load is 0.18 m, the maximum uniformly distributed load (throughout the span) the beam can carry will be _____kN/m. (Neglect the self weight of the beam).Correct answer is '35-36'. Can you explain this answer? has been provided alongside types of A simply supported rectangular prestressed concrete beam of span 9 m has to be prestressed with a force of 2000 kN. The profile of the cable is parabolic with zero eccentricity at ends. If the maximum dip (allowable) of the tendon at the mid-span to balance the external load is 0.18 m, the maximum uniformly distributed load (throughout the span) the beam can carry will be _____kN/m. (Neglect the self weight of the beam).Correct answer is '35-36'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A simply supported rectangular prestressed concrete beam of span 9 m has to be prestressed with a force of 2000 kN. The profile of the cable is parabolic with zero eccentricity at ends. If the maximum dip (allowable) of the tendon at the mid-span to balance the external load is 0.18 m, the maximum uniformly distributed load (throughout the span) the beam can carry will be _____kN/m. (Neglect the self weight of the beam).Correct answer is '35-36'. Can you explain this answer? tests, examples and also practice Civil Engineering (CE) tests.

|
Explore Courses for Civil Engineering (CE) exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.





















