Class 12 Exam > Class 12 Questions > Is a function defined by f(x)=|x| , a continu...
Start Learning for Free
Is a function defined by f(x)=|x| , a continuous function ?
Most Upvoted Answer
Is a function defined by f(x)=|x| , a continuous function ?
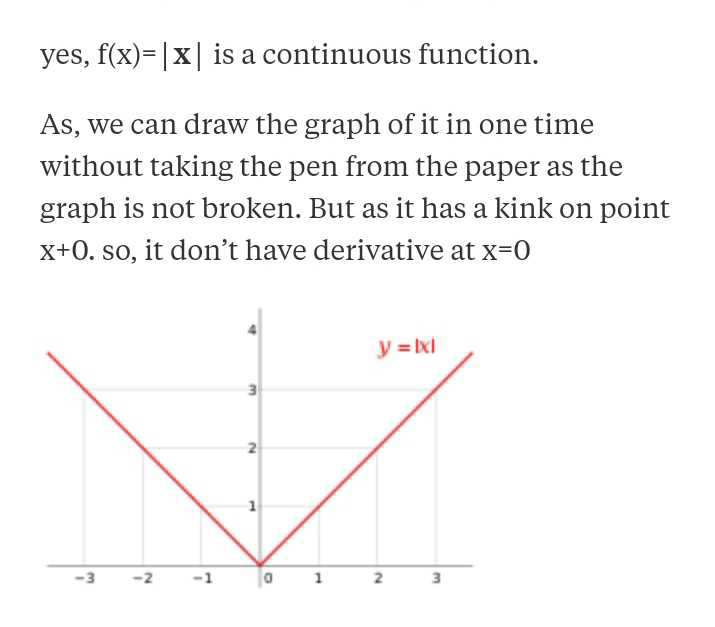
Community Answer
Is a function defined by f(x)=|x| , a continuous function ?
Introduction:
To determine if the function f(x) = |x| is continuous, we need to analyze its behavior at different points and intervals. Continuity is a fundamental concept in calculus that refers to the absence of any sudden jumps, holes, or vertical asymptotes in a function's graph.
Analysis:
1. Continuity at x = 0:
- Let's consider the function f(x) = |x|.
- At x = 0, the value of f(x) is also 0 since the absolute value of 0 is 0.
- The left-hand limit as x approaches 0 is also 0, since f(x) approaches 0 from the left side.
- The right-hand limit as x approaches 0 is also 0, since f(x) approaches 0 from the right side.
- Therefore, the limit of f(x) as x approaches 0 exists and is equal to 0.
- Consequently, f(x) is continuous at x = 0.
2. Continuity on the positive x-axis (x > 0):
- For x > 0, the function f(x) = x since the absolute value of a positive number is the number itself.
- The function f(x) = x is continuous on the positive x-axis as it is a linear function with no jumps, holes, or vertical asymptotes.
3. Continuity on the negative x-axis (x < />
- For x < 0,="" the="" function="" f(x)="-x" since="" the="" absolute="" value="" of="" a="" negative="" number="" is="" the="" number="" with="" its="" sign="" />
- The function f(x) = -x is also continuous on the negative x-axis as it is a linear function without any discontinuities.
Conclusion:
Considering the analysis above, we can conclude that the function f(x) = |x| is continuous for all real numbers. It is continuous at x = 0 and also on the positive and negative x-axes. The graph of f(x) consists of two linear segments meeting at the origin without any sudden jumps, holes, or vertical asymptotes.
To determine if the function f(x) = |x| is continuous, we need to analyze its behavior at different points and intervals. Continuity is a fundamental concept in calculus that refers to the absence of any sudden jumps, holes, or vertical asymptotes in a function's graph.
Analysis:
1. Continuity at x = 0:
- Let's consider the function f(x) = |x|.
- At x = 0, the value of f(x) is also 0 since the absolute value of 0 is 0.
- The left-hand limit as x approaches 0 is also 0, since f(x) approaches 0 from the left side.
- The right-hand limit as x approaches 0 is also 0, since f(x) approaches 0 from the right side.
- Therefore, the limit of f(x) as x approaches 0 exists and is equal to 0.
- Consequently, f(x) is continuous at x = 0.
2. Continuity on the positive x-axis (x > 0):
- For x > 0, the function f(x) = x since the absolute value of a positive number is the number itself.
- The function f(x) = x is continuous on the positive x-axis as it is a linear function with no jumps, holes, or vertical asymptotes.
3. Continuity on the negative x-axis (x < />
- For x < 0,="" the="" function="" f(x)="-x" since="" the="" absolute="" value="" of="" a="" negative="" number="" is="" the="" number="" with="" its="" sign="" />
- The function f(x) = -x is also continuous on the negative x-axis as it is a linear function without any discontinuities.
Conclusion:
Considering the analysis above, we can conclude that the function f(x) = |x| is continuous for all real numbers. It is continuous at x = 0 and also on the positive and negative x-axes. The graph of f(x) consists of two linear segments meeting at the origin without any sudden jumps, holes, or vertical asymptotes.

|
Explore Courses for Class 12 exam
|

|
Similar Class 12 Doubts
Question Description
Is a function defined by f(x)=|x| , a continuous function ? for Class 12 2025 is part of Class 12 preparation. The Question and answers have been prepared according to the Class 12 exam syllabus. Information about Is a function defined by f(x)=|x| , a continuous function ? covers all topics & solutions for Class 12 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Is a function defined by f(x)=|x| , a continuous function ?.
Is a function defined by f(x)=|x| , a continuous function ? for Class 12 2025 is part of Class 12 preparation. The Question and answers have been prepared according to the Class 12 exam syllabus. Information about Is a function defined by f(x)=|x| , a continuous function ? covers all topics & solutions for Class 12 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Is a function defined by f(x)=|x| , a continuous function ?.
Solutions for Is a function defined by f(x)=|x| , a continuous function ? in English & in Hindi are available as part of our courses for Class 12.
Download more important topics, notes, lectures and mock test series for Class 12 Exam by signing up for free.
Here you can find the meaning of Is a function defined by f(x)=|x| , a continuous function ? defined & explained in the simplest way possible. Besides giving the explanation of
Is a function defined by f(x)=|x| , a continuous function ?, a detailed solution for Is a function defined by f(x)=|x| , a continuous function ? has been provided alongside types of Is a function defined by f(x)=|x| , a continuous function ? theory, EduRev gives you an
ample number of questions to practice Is a function defined by f(x)=|x| , a continuous function ? tests, examples and also practice Class 12 tests.

|
Explore Courses for Class 12 exam
|

|
Signup to solve all Doubts
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.




















