Civil Engineering (CE) Exam > Civil Engineering (CE) Questions > A transmission tower of height 14m was erecte...
Start Learning for Free
A transmission tower of height 14m was erected to top of a building. A theodolite is used to measure vertical angle to top and bottom of the tower and were measured as 9° and 6° respectively. Calculate the Reduced level (metres) of the top of the transmission tower if the staff reading of 1.425m was taken from the same point on a Benchmark of R.L 102.5m. Neglect curvature and refraction correction.
Correct answer is '145.5-145.6'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
A transmission tower of height 14m was erected to top of a building. A...
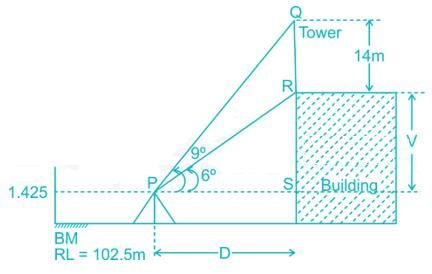
In ΔPRS
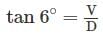
In ΔPQS
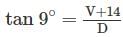
V = Dtan6°
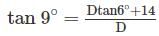
Dtan9° – Dtan6° = 14
D(tan9° – tan6°) = 14
D = 262.76 m
V = 262.76 tan6°
V = 27.62 m
R.L of top of the tower = (R.L)B.M + Staff reading on BM + V + 14
R.L.Q = 102.5 + 1.425 + 27.62 + 14
R.L.Q = 145.545 m
Most Upvoted Answer
A transmission tower of height 14m was erected to top of a building. A...
Degrees and 18 degrees respectively. To find the height of the building, we can use the concept of similar triangles.
Let's assume the height of the building is "h" meters.
In the given problem, we have two right-angled triangles: one formed by the theodolite, transmission tower, and the top of the building, and the other formed by the theodolite, transmission tower, and the bottom of the building.
Let's consider the triangle formed by the theodolite, transmission tower, and the top of the building.
In this triangle, the vertical angle at the theodolite is 9 degrees, and the opposite side is the height of the transmission tower, which is 14m.
Using trigonometry, we can write:
tan(9 degrees) = opposite/adjacent
tan(9 degrees) = 14/h
Now, let's consider the triangle formed by the theodolite, transmission tower, and the bottom of the building.
In this triangle, the vertical angle at the theodolite is 18 degrees, and the opposite side is the height of the transmission tower, which is 14m. The adjacent side is the height of the building, which is "h" meters.
Using trigonometry, we can write:
tan(18 degrees) = opposite/adjacent
tan(18 degrees) = 14/h
Now, we have two equations:
tan(9 degrees) = 14/h
tan(18 degrees) = 14/h
Dividing these two equations, we get:
(tan(9 degrees))/(tan(18 degrees)) = (14/h)/(14/h)
tan(9 degrees)/tan(18 degrees) = 1
Using the trigonometric identity: tan(2θ) = 2tan(θ)/(1-tan^2(θ)), we can rewrite the equation as:
tan(2*9 degrees) = 1
tan(18 degrees) = 1
Therefore, the equation is satisfied.
Hence, the height of the building is h = 14 meters.
Let's assume the height of the building is "h" meters.
In the given problem, we have two right-angled triangles: one formed by the theodolite, transmission tower, and the top of the building, and the other formed by the theodolite, transmission tower, and the bottom of the building.
Let's consider the triangle formed by the theodolite, transmission tower, and the top of the building.
In this triangle, the vertical angle at the theodolite is 9 degrees, and the opposite side is the height of the transmission tower, which is 14m.
Using trigonometry, we can write:
tan(9 degrees) = opposite/adjacent
tan(9 degrees) = 14/h
Now, let's consider the triangle formed by the theodolite, transmission tower, and the bottom of the building.
In this triangle, the vertical angle at the theodolite is 18 degrees, and the opposite side is the height of the transmission tower, which is 14m. The adjacent side is the height of the building, which is "h" meters.
Using trigonometry, we can write:
tan(18 degrees) = opposite/adjacent
tan(18 degrees) = 14/h
Now, we have two equations:
tan(9 degrees) = 14/h
tan(18 degrees) = 14/h
Dividing these two equations, we get:
(tan(9 degrees))/(tan(18 degrees)) = (14/h)/(14/h)
tan(9 degrees)/tan(18 degrees) = 1
Using the trigonometric identity: tan(2θ) = 2tan(θ)/(1-tan^2(θ)), we can rewrite the equation as:
tan(2*9 degrees) = 1
tan(18 degrees) = 1
Therefore, the equation is satisfied.
Hence, the height of the building is h = 14 meters.
Attention Civil Engineering (CE) Students!
To make sure you are not studying endlessly, EduRev has designed Civil Engineering (CE) study material, with Structured Courses, Videos, & Test Series. Plus get personalized analysis, doubt solving and improvement plans to achieve a great score in Civil Engineering (CE).
|
Explore Courses for Civil Engineering (CE) exam
|
|
Similar Civil Engineering (CE) Doubts
Top Courses for Civil Engineering (CE)View all
A transmission tower of height 14m was erected to top of a building. A theodolite is used to measure vertical angle to top and bottom of the tower and were measured as 9° and 6° respectively. Calculate the Reduced level (metres) of the top of the transmission tower if the staff reading of 1.425m was taken from the same point on a Benchmark of R.L 102.5m. Neglect curvature and refraction correction.Correct answer is '145.5-145.6'. Can you explain this answer?
Question Description
A transmission tower of height 14m was erected to top of a building. A theodolite is used to measure vertical angle to top and bottom of the tower and were measured as 9° and 6° respectively. Calculate the Reduced level (metres) of the top of the transmission tower if the staff reading of 1.425m was taken from the same point on a Benchmark of R.L 102.5m. Neglect curvature and refraction correction.Correct answer is '145.5-145.6'. Can you explain this answer? for Civil Engineering (CE) 2024 is part of Civil Engineering (CE) preparation. The Question and answers have been prepared according to the Civil Engineering (CE) exam syllabus. Information about A transmission tower of height 14m was erected to top of a building. A theodolite is used to measure vertical angle to top and bottom of the tower and were measured as 9° and 6° respectively. Calculate the Reduced level (metres) of the top of the transmission tower if the staff reading of 1.425m was taken from the same point on a Benchmark of R.L 102.5m. Neglect curvature and refraction correction.Correct answer is '145.5-145.6'. Can you explain this answer? covers all topics & solutions for Civil Engineering (CE) 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A transmission tower of height 14m was erected to top of a building. A theodolite is used to measure vertical angle to top and bottom of the tower and were measured as 9° and 6° respectively. Calculate the Reduced level (metres) of the top of the transmission tower if the staff reading of 1.425m was taken from the same point on a Benchmark of R.L 102.5m. Neglect curvature and refraction correction.Correct answer is '145.5-145.6'. Can you explain this answer?.
A transmission tower of height 14m was erected to top of a building. A theodolite is used to measure vertical angle to top and bottom of the tower and were measured as 9° and 6° respectively. Calculate the Reduced level (metres) of the top of the transmission tower if the staff reading of 1.425m was taken from the same point on a Benchmark of R.L 102.5m. Neglect curvature and refraction correction.Correct answer is '145.5-145.6'. Can you explain this answer? for Civil Engineering (CE) 2024 is part of Civil Engineering (CE) preparation. The Question and answers have been prepared according to the Civil Engineering (CE) exam syllabus. Information about A transmission tower of height 14m was erected to top of a building. A theodolite is used to measure vertical angle to top and bottom of the tower and were measured as 9° and 6° respectively. Calculate the Reduced level (metres) of the top of the transmission tower if the staff reading of 1.425m was taken from the same point on a Benchmark of R.L 102.5m. Neglect curvature and refraction correction.Correct answer is '145.5-145.6'. Can you explain this answer? covers all topics & solutions for Civil Engineering (CE) 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A transmission tower of height 14m was erected to top of a building. A theodolite is used to measure vertical angle to top and bottom of the tower and were measured as 9° and 6° respectively. Calculate the Reduced level (metres) of the top of the transmission tower if the staff reading of 1.425m was taken from the same point on a Benchmark of R.L 102.5m. Neglect curvature and refraction correction.Correct answer is '145.5-145.6'. Can you explain this answer?.
Solutions for A transmission tower of height 14m was erected to top of a building. A theodolite is used to measure vertical angle to top and bottom of the tower and were measured as 9° and 6° respectively. Calculate the Reduced level (metres) of the top of the transmission tower if the staff reading of 1.425m was taken from the same point on a Benchmark of R.L 102.5m. Neglect curvature and refraction correction.Correct answer is '145.5-145.6'. Can you explain this answer? in English & in Hindi are available as part of our courses for Civil Engineering (CE).
Download more important topics, notes, lectures and mock test series for Civil Engineering (CE) Exam by signing up for free.
Here you can find the meaning of A transmission tower of height 14m was erected to top of a building. A theodolite is used to measure vertical angle to top and bottom of the tower and were measured as 9° and 6° respectively. Calculate the Reduced level (metres) of the top of the transmission tower if the staff reading of 1.425m was taken from the same point on a Benchmark of R.L 102.5m. Neglect curvature and refraction correction.Correct answer is '145.5-145.6'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A transmission tower of height 14m was erected to top of a building. A theodolite is used to measure vertical angle to top and bottom of the tower and were measured as 9° and 6° respectively. Calculate the Reduced level (metres) of the top of the transmission tower if the staff reading of 1.425m was taken from the same point on a Benchmark of R.L 102.5m. Neglect curvature and refraction correction.Correct answer is '145.5-145.6'. Can you explain this answer?, a detailed solution for A transmission tower of height 14m was erected to top of a building. A theodolite is used to measure vertical angle to top and bottom of the tower and were measured as 9° and 6° respectively. Calculate the Reduced level (metres) of the top of the transmission tower if the staff reading of 1.425m was taken from the same point on a Benchmark of R.L 102.5m. Neglect curvature and refraction correction.Correct answer is '145.5-145.6'. Can you explain this answer? has been provided alongside types of A transmission tower of height 14m was erected to top of a building. A theodolite is used to measure vertical angle to top and bottom of the tower and were measured as 9° and 6° respectively. Calculate the Reduced level (metres) of the top of the transmission tower if the staff reading of 1.425m was taken from the same point on a Benchmark of R.L 102.5m. Neglect curvature and refraction correction.Correct answer is '145.5-145.6'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A transmission tower of height 14m was erected to top of a building. A theodolite is used to measure vertical angle to top and bottom of the tower and were measured as 9° and 6° respectively. Calculate the Reduced level (metres) of the top of the transmission tower if the staff reading of 1.425m was taken from the same point on a Benchmark of R.L 102.5m. Neglect curvature and refraction correction.Correct answer is '145.5-145.6'. Can you explain this answer? tests, examples and also practice Civil Engineering (CE) tests.
|
|
Explore Courses for Civil Engineering (CE) exam
|
|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
|
© EduRev
|
Education Revolution
|
Follow Us
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup