Railways Exam > Railways Questions > A block A is released from the top of smooth ...
Start Learning for Free
A block A is released from the top of smooth inclined plane and slides down the plane. Another block B is dropped from the same point and falls vertically downwards. Which one of the following statements will be true if the friction offered by air is negligible?
- a)Both blocks will reach the ground at the same time
- b)Block A reaches the ground earlier that block B
- c)Both blocks will reach the ground with the same speed
- d)Block B reaches the ground with a higher speed than block A
Correct answer is option 'C'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
A block A is released from the top of smooth inclined plane and slides...
Consider a block of mass m lying on a frictionless inclined plane of length AB = L, height = h and angle of inclination θ.
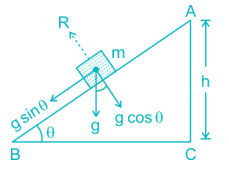
When the block is released, it moves down the plane under a force mg sin θ.
Hence the acceleration of the block down the plane is
a = g sin θ
If the block starts from rest from point A, then its velocity when it reaches the bottom B is given by
v2 – u2 = 2as
v2 – 0 = 2aL

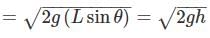
For the block which falls vertically downward of height, h:
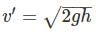
So, speed of both the blocks will be same.

When the block is released, it moves down the plane under a force mg sin θ.
Hence the acceleration of the block down the plane is
a = g sin θ
If the block starts from rest from point A, then its velocity when it reaches the bottom B is given by
v2 – u2 = 2as
v2 – 0 = 2aL

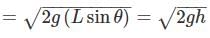
For the block which falls vertically downward of height, h:
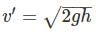
So, speed of both the blocks will be same.
Most Upvoted Answer
A block A is released from the top of smooth inclined plane and slides...
Explanation:
When a block is released from the top of a smooth inclined plane, it will slide down the plane due to the force of gravity. On the other hand, when a block is dropped vertically downwards, it will also fall due to the force of gravity. Let's analyze the motion of each block separately.
Block A sliding down the inclined plane:
- The force acting on block A is its weight, which can be resolved into two components: one parallel to the inclined plane (mg*sinθ) and one perpendicular to the inclined plane (mg*cosθ).
- The component of the weight parallel to the inclined plane (mg*sinθ) will cause the block to accelerate down the plane.
- The acceleration of block A can be calculated using the equation a = g*sinθ, where g is the acceleration due to gravity and θ is the angle of inclination.
- The speed of block A at any point can be calculated using the equation v = u + at, where u is the initial speed (0 in this case), a is the acceleration, and t is the time taken.
- As the block slides down the inclined plane, it will gain speed and reach the bottom of the plane in a certain time.
Block B falling vertically downwards:
- When block B is dropped vertically downwards, it will fall due to the force of gravity.
- The only force acting on block B is its weight, which is mg, where m is the mass of the block and g is the acceleration due to gravity.
- The acceleration of block B is equal to the acceleration due to gravity, which is approximately 9.8 m/s².
- The speed of block B at any point can be calculated using the equation v = u + at, where u is the initial speed (0 in this case), a is the acceleration, and t is the time taken.
- As block B falls vertically downwards, it will gain speed and reach the ground in a certain time.
Comparison between the two blocks:
- Both blocks are subject to the same acceleration due to gravity.
- The time taken for both blocks to reach the ground will be the same because the acceleration due to gravity is the same and the distance traveled is also the same (assuming the height of the inclined plane and the height from which block B is dropped are the same).
- However, the speed at which both blocks reach the ground will be different.
- Block A will reach the ground with a higher speed than block B because it has been accelerating down the inclined plane, whereas block B has been falling vertically downwards without any additional acceleration.
Therefore, the correct statement is that both blocks will reach the ground with the same speed (option C).
When a block is released from the top of a smooth inclined plane, it will slide down the plane due to the force of gravity. On the other hand, when a block is dropped vertically downwards, it will also fall due to the force of gravity. Let's analyze the motion of each block separately.
Block A sliding down the inclined plane:
- The force acting on block A is its weight, which can be resolved into two components: one parallel to the inclined plane (mg*sinθ) and one perpendicular to the inclined plane (mg*cosθ).
- The component of the weight parallel to the inclined plane (mg*sinθ) will cause the block to accelerate down the plane.
- The acceleration of block A can be calculated using the equation a = g*sinθ, where g is the acceleration due to gravity and θ is the angle of inclination.
- The speed of block A at any point can be calculated using the equation v = u + at, where u is the initial speed (0 in this case), a is the acceleration, and t is the time taken.
- As the block slides down the inclined plane, it will gain speed and reach the bottom of the plane in a certain time.
Block B falling vertically downwards:
- When block B is dropped vertically downwards, it will fall due to the force of gravity.
- The only force acting on block B is its weight, which is mg, where m is the mass of the block and g is the acceleration due to gravity.
- The acceleration of block B is equal to the acceleration due to gravity, which is approximately 9.8 m/s².
- The speed of block B at any point can be calculated using the equation v = u + at, where u is the initial speed (0 in this case), a is the acceleration, and t is the time taken.
- As block B falls vertically downwards, it will gain speed and reach the ground in a certain time.
Comparison between the two blocks:
- Both blocks are subject to the same acceleration due to gravity.
- The time taken for both blocks to reach the ground will be the same because the acceleration due to gravity is the same and the distance traveled is also the same (assuming the height of the inclined plane and the height from which block B is dropped are the same).
- However, the speed at which both blocks reach the ground will be different.
- Block A will reach the ground with a higher speed than block B because it has been accelerating down the inclined plane, whereas block B has been falling vertically downwards without any additional acceleration.
Therefore, the correct statement is that both blocks will reach the ground with the same speed (option C).
Attention Railways Students!
To make sure you are not studying endlessly, EduRev has designed Railways study material, with Structured Courses, Videos, & Test Series. Plus get personalized analysis, doubt solving and improvement plans to achieve a great score in Railways.

|
Explore Courses for Railways exam
|

|
Similar Railways Doubts
A block A is released from the top of smooth inclined plane and slides down the plane. Another block B is dropped from the same point and falls vertically downwards. Which one of the following statements will be true if the friction offered by air is negligible?a)Both blocks will reach the ground at the same timeb)Block A reaches the ground earlier that block Bc)Both blocks will reach the ground with the same speedd)Block B reaches the ground with a higher speed than block ACorrect answer is option 'C'. Can you explain this answer?
Question Description
A block A is released from the top of smooth inclined plane and slides down the plane. Another block B is dropped from the same point and falls vertically downwards. Which one of the following statements will be true if the friction offered by air is negligible?a)Both blocks will reach the ground at the same timeb)Block A reaches the ground earlier that block Bc)Both blocks will reach the ground with the same speedd)Block B reaches the ground with a higher speed than block ACorrect answer is option 'C'. Can you explain this answer? for Railways 2024 is part of Railways preparation. The Question and answers have been prepared according to the Railways exam syllabus. Information about A block A is released from the top of smooth inclined plane and slides down the plane. Another block B is dropped from the same point and falls vertically downwards. Which one of the following statements will be true if the friction offered by air is negligible?a)Both blocks will reach the ground at the same timeb)Block A reaches the ground earlier that block Bc)Both blocks will reach the ground with the same speedd)Block B reaches the ground with a higher speed than block ACorrect answer is option 'C'. Can you explain this answer? covers all topics & solutions for Railways 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A block A is released from the top of smooth inclined plane and slides down the plane. Another block B is dropped from the same point and falls vertically downwards. Which one of the following statements will be true if the friction offered by air is negligible?a)Both blocks will reach the ground at the same timeb)Block A reaches the ground earlier that block Bc)Both blocks will reach the ground with the same speedd)Block B reaches the ground with a higher speed than block ACorrect answer is option 'C'. Can you explain this answer?.
A block A is released from the top of smooth inclined plane and slides down the plane. Another block B is dropped from the same point and falls vertically downwards. Which one of the following statements will be true if the friction offered by air is negligible?a)Both blocks will reach the ground at the same timeb)Block A reaches the ground earlier that block Bc)Both blocks will reach the ground with the same speedd)Block B reaches the ground with a higher speed than block ACorrect answer is option 'C'. Can you explain this answer? for Railways 2024 is part of Railways preparation. The Question and answers have been prepared according to the Railways exam syllabus. Information about A block A is released from the top of smooth inclined plane and slides down the plane. Another block B is dropped from the same point and falls vertically downwards. Which one of the following statements will be true if the friction offered by air is negligible?a)Both blocks will reach the ground at the same timeb)Block A reaches the ground earlier that block Bc)Both blocks will reach the ground with the same speedd)Block B reaches the ground with a higher speed than block ACorrect answer is option 'C'. Can you explain this answer? covers all topics & solutions for Railways 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A block A is released from the top of smooth inclined plane and slides down the plane. Another block B is dropped from the same point and falls vertically downwards. Which one of the following statements will be true if the friction offered by air is negligible?a)Both blocks will reach the ground at the same timeb)Block A reaches the ground earlier that block Bc)Both blocks will reach the ground with the same speedd)Block B reaches the ground with a higher speed than block ACorrect answer is option 'C'. Can you explain this answer?.
Solutions for A block A is released from the top of smooth inclined plane and slides down the plane. Another block B is dropped from the same point and falls vertically downwards. Which one of the following statements will be true if the friction offered by air is negligible?a)Both blocks will reach the ground at the same timeb)Block A reaches the ground earlier that block Bc)Both blocks will reach the ground with the same speedd)Block B reaches the ground with a higher speed than block ACorrect answer is option 'C'. Can you explain this answer? in English & in Hindi are available as part of our courses for Railways.
Download more important topics, notes, lectures and mock test series for Railways Exam by signing up for free.
Here you can find the meaning of A block A is released from the top of smooth inclined plane and slides down the plane. Another block B is dropped from the same point and falls vertically downwards. Which one of the following statements will be true if the friction offered by air is negligible?a)Both blocks will reach the ground at the same timeb)Block A reaches the ground earlier that block Bc)Both blocks will reach the ground with the same speedd)Block B reaches the ground with a higher speed than block ACorrect answer is option 'C'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A block A is released from the top of smooth inclined plane and slides down the plane. Another block B is dropped from the same point and falls vertically downwards. Which one of the following statements will be true if the friction offered by air is negligible?a)Both blocks will reach the ground at the same timeb)Block A reaches the ground earlier that block Bc)Both blocks will reach the ground with the same speedd)Block B reaches the ground with a higher speed than block ACorrect answer is option 'C'. Can you explain this answer?, a detailed solution for A block A is released from the top of smooth inclined plane and slides down the plane. Another block B is dropped from the same point and falls vertically downwards. Which one of the following statements will be true if the friction offered by air is negligible?a)Both blocks will reach the ground at the same timeb)Block A reaches the ground earlier that block Bc)Both blocks will reach the ground with the same speedd)Block B reaches the ground with a higher speed than block ACorrect answer is option 'C'. Can you explain this answer? has been provided alongside types of A block A is released from the top of smooth inclined plane and slides down the plane. Another block B is dropped from the same point and falls vertically downwards. Which one of the following statements will be true if the friction offered by air is negligible?a)Both blocks will reach the ground at the same timeb)Block A reaches the ground earlier that block Bc)Both blocks will reach the ground with the same speedd)Block B reaches the ground with a higher speed than block ACorrect answer is option 'C'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A block A is released from the top of smooth inclined plane and slides down the plane. Another block B is dropped from the same point and falls vertically downwards. Which one of the following statements will be true if the friction offered by air is negligible?a)Both blocks will reach the ground at the same timeb)Block A reaches the ground earlier that block Bc)Both blocks will reach the ground with the same speedd)Block B reaches the ground with a higher speed than block ACorrect answer is option 'C'. Can you explain this answer? tests, examples and also practice Railways tests.

|
Explore Courses for Railways exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
























