Class 11 Exam > Class 11 Questions > The area under the velocity-time curve betwee...
Start Learning for Free
The area under the velocity-time curve between times t1 and t2 is equal to the.
- a)average velocity of the object during that interval of time
- b)path length of the object during that interval of time
- c)velocity of the object during that interval of time
- d)displacement of the object during that interval of time
Correct answer is option 'D'. Can you explain this answer?
Verified Answer
The area under the velocity-time curve between times t1 and t2 is equa...
Explanation:The area under the velocity-time curve between times t1and t2 is equal to the displacement of the object during that interval of time.
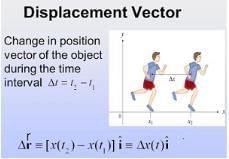
Most Upvoted Answer
The area under the velocity-time curve between times t1 and t2 is equa...
Explanation:
The area under the velocity-time curve represents the displacement of the object during that interval of time. This can be explained using the basic concept of calculus and the relationship between velocity and displacement.
Understanding the velocity-time curve:
The velocity-time curve represents how the velocity of an object changes over time. The velocity is plotted on the y-axis, and time is plotted on the x-axis. The shape of the curve depends on the motion of the object. For example, if the object is moving with constant velocity, the curve will be a straight line parallel to the x-axis. If the object is accelerating or decelerating, the curve will be curved.
Using calculus to find displacement:
To find the displacement of an object during a given interval of time, we can use calculus and integrate the velocity function with respect to time. Integration represents the area under the curve.
Explanation of the options:
a) Average velocity of the object during that interval of time: The average velocity is calculated by dividing the total displacement by the total time. It is not directly related to the area under the velocity-time curve.
b) Path length of the object during that interval of time: The path length is the total distance traveled by the object. It is not directly related to the area under the velocity-time curve.
c) Velocity of the object during that interval of time: The velocity of the object at a specific time can be determined from the velocity-time curve. However, the area under the curve does not represent the instantaneous velocity at any particular time.
d) Displacement of the object during that interval of time: The area under the velocity-time curve represents the change in displacement of the object during that interval of time. By integrating the velocity function, we can find the total area under the curve, which gives us the displacement.
Conclusion:
The area under the velocity-time curve between times t1 and t2 represents the displacement of the object during that interval of time. This is because integration of the velocity function gives us the total area under the curve, which represents the change in displacement.
The area under the velocity-time curve represents the displacement of the object during that interval of time. This can be explained using the basic concept of calculus and the relationship between velocity and displacement.
Understanding the velocity-time curve:
The velocity-time curve represents how the velocity of an object changes over time. The velocity is plotted on the y-axis, and time is plotted on the x-axis. The shape of the curve depends on the motion of the object. For example, if the object is moving with constant velocity, the curve will be a straight line parallel to the x-axis. If the object is accelerating or decelerating, the curve will be curved.
Using calculus to find displacement:
To find the displacement of an object during a given interval of time, we can use calculus and integrate the velocity function with respect to time. Integration represents the area under the curve.
Explanation of the options:
a) Average velocity of the object during that interval of time: The average velocity is calculated by dividing the total displacement by the total time. It is not directly related to the area under the velocity-time curve.
b) Path length of the object during that interval of time: The path length is the total distance traveled by the object. It is not directly related to the area under the velocity-time curve.
c) Velocity of the object during that interval of time: The velocity of the object at a specific time can be determined from the velocity-time curve. However, the area under the curve does not represent the instantaneous velocity at any particular time.
d) Displacement of the object during that interval of time: The area under the velocity-time curve represents the change in displacement of the object during that interval of time. By integrating the velocity function, we can find the total area under the curve, which gives us the displacement.
Conclusion:
The area under the velocity-time curve between times t1 and t2 represents the displacement of the object during that interval of time. This is because integration of the velocity function gives us the total area under the curve, which represents the change in displacement.

|
Explore Courses for Class 11 exam
|

|
Question Description
The area under the velocity-time curve between times t1 and t2 is equal to the.a)average velocity of the object during that interval of timeb)path length of the object during that interval of timec)velocity of the object during that interval of timed)displacement of the object during that interval of timeCorrect answer is option 'D'. Can you explain this answer? for Class 11 2025 is part of Class 11 preparation. The Question and answers have been prepared according to the Class 11 exam syllabus. Information about The area under the velocity-time curve between times t1 and t2 is equal to the.a)average velocity of the object during that interval of timeb)path length of the object during that interval of timec)velocity of the object during that interval of timed)displacement of the object during that interval of timeCorrect answer is option 'D'. Can you explain this answer? covers all topics & solutions for Class 11 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The area under the velocity-time curve between times t1 and t2 is equal to the.a)average velocity of the object during that interval of timeb)path length of the object during that interval of timec)velocity of the object during that interval of timed)displacement of the object during that interval of timeCorrect answer is option 'D'. Can you explain this answer?.
The area under the velocity-time curve between times t1 and t2 is equal to the.a)average velocity of the object during that interval of timeb)path length of the object during that interval of timec)velocity of the object during that interval of timed)displacement of the object during that interval of timeCorrect answer is option 'D'. Can you explain this answer? for Class 11 2025 is part of Class 11 preparation. The Question and answers have been prepared according to the Class 11 exam syllabus. Information about The area under the velocity-time curve between times t1 and t2 is equal to the.a)average velocity of the object during that interval of timeb)path length of the object during that interval of timec)velocity of the object during that interval of timed)displacement of the object during that interval of timeCorrect answer is option 'D'. Can you explain this answer? covers all topics & solutions for Class 11 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The area under the velocity-time curve between times t1 and t2 is equal to the.a)average velocity of the object during that interval of timeb)path length of the object during that interval of timec)velocity of the object during that interval of timed)displacement of the object during that interval of timeCorrect answer is option 'D'. Can you explain this answer?.
Solutions for The area under the velocity-time curve between times t1 and t2 is equal to the.a)average velocity of the object during that interval of timeb)path length of the object during that interval of timec)velocity of the object during that interval of timed)displacement of the object during that interval of timeCorrect answer is option 'D'. Can you explain this answer? in English & in Hindi are available as part of our courses for Class 11.
Download more important topics, notes, lectures and mock test series for Class 11 Exam by signing up for free.
Here you can find the meaning of The area under the velocity-time curve between times t1 and t2 is equal to the.a)average velocity of the object during that interval of timeb)path length of the object during that interval of timec)velocity of the object during that interval of timed)displacement of the object during that interval of timeCorrect answer is option 'D'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
The area under the velocity-time curve between times t1 and t2 is equal to the.a)average velocity of the object during that interval of timeb)path length of the object during that interval of timec)velocity of the object during that interval of timed)displacement of the object during that interval of timeCorrect answer is option 'D'. Can you explain this answer?, a detailed solution for The area under the velocity-time curve between times t1 and t2 is equal to the.a)average velocity of the object during that interval of timeb)path length of the object during that interval of timec)velocity of the object during that interval of timed)displacement of the object during that interval of timeCorrect answer is option 'D'. Can you explain this answer? has been provided alongside types of The area under the velocity-time curve between times t1 and t2 is equal to the.a)average velocity of the object during that interval of timeb)path length of the object during that interval of timec)velocity of the object during that interval of timed)displacement of the object during that interval of timeCorrect answer is option 'D'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice The area under the velocity-time curve between times t1 and t2 is equal to the.a)average velocity of the object during that interval of timeb)path length of the object during that interval of timec)velocity of the object during that interval of timed)displacement of the object during that interval of timeCorrect answer is option 'D'. Can you explain this answer? tests, examples and also practice Class 11 tests.

|
Explore Courses for Class 11 exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.























