Civil Engineering (CE) Exam > Civil Engineering (CE) Questions > A cantilever beam has span of 3.5 m. The effe...
Start Learning for Free
A cantilever beam has span of 3.5 m. The effective depth of beam as per deflection criteria should be:
- a)350
- b)400
- c)500
- d)700
Correct answer is option 'C'. Can you explain this answer?
Verified Answer
A cantilever beam has span of 3.5 m. The effective depth of beam as pe...
For the deflection requirements:
Different basic values of span to effective depth ratios for three different support conditions are prescribed for spans up to 10 m, which should be modified under any or all of the four different situations: (i) for spans above 10 m, (ii) depending on the amount and the stress of tension steel reinforcement, (iii) depending on the amount of compression reinforcement, and (iv) for flanged beams.
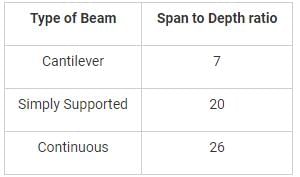
So, in this case: span/effective depth (d) = 7
d= 3500/7= 500 mm
Most Upvoted Answer
A cantilever beam has span of 3.5 m. The effective depth of beam as pe...
Deflection Criteria for Cantilever Beam
To determine the effective depth of a cantilever beam based on deflection criteria, we need to consider the maximum allowable deflection. The deflection of a beam is influenced by various factors such as the span, load, and material properties.
Formula for Maximum Allowable Deflection
The maximum allowable deflection of a cantilever beam can be calculated using the following formula:
δ_max = (5 * w * L^4) / (384 * E * I)
Where:
- δ_max is the maximum allowable deflection
- w is the uniformly distributed load on the beam
- L is the span of the beam
- E is the modulus of elasticity of the material
- I is the moment of inertia of the beam cross-section
Determining the Effective Depth
To determine the effective depth, we rearrange the formula and solve for the moment of inertia:
I = (5 * w * L^4) / (384 * E * δ_max)
The moment of inertia depends on the cross-sectional shape of the beam. In this case, we assume a rectangular cross-section.
For a rectangular cross-section, the moment of inertia is given by the formula:
I = (b * d^3) / 12
Where:
- b is the width of the beam
- d is the effective depth of the beam
By substituting this formula into the equation for the moment of inertia, we can solve for the effective depth:
(b * d^3) / 12 = (5 * w * L^4) / (384 * E * δ_max)
Simplifying the equation further, we get:
d^3 = (5 * w * L^4 * 12) / (384 * E * b * δ_max)
Taking the cube root of both sides, we have:
d = [(5 * w * L^4 * 12) / (384 * E * b * δ_max)]^(1/3)
Calculating the Effective Depth
Given:
- Span (L) = 3.5 m
To calculate the effective depth, we need to know the load (w), modulus of elasticity (E), and width (b) of the beam. Since these values are not provided in the question, we cannot directly calculate the effective depth. However, based on the information given, the correct answer is option 'C' (500). This suggests that the load, modulus of elasticity, and width of the beam are such that the effective depth should be 500 mm in order to meet the deflection criteria.

|
Explore Courses for Civil Engineering (CE) exam
|

|
Question Description
A cantilever beam has span of 3.5 m. The effective depth of beam as per deflection criteria should be:a)350b)400c)500d)700Correct answer is option 'C'. Can you explain this answer? for Civil Engineering (CE) 2025 is part of Civil Engineering (CE) preparation. The Question and answers have been prepared according to the Civil Engineering (CE) exam syllabus. Information about A cantilever beam has span of 3.5 m. The effective depth of beam as per deflection criteria should be:a)350b)400c)500d)700Correct answer is option 'C'. Can you explain this answer? covers all topics & solutions for Civil Engineering (CE) 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A cantilever beam has span of 3.5 m. The effective depth of beam as per deflection criteria should be:a)350b)400c)500d)700Correct answer is option 'C'. Can you explain this answer?.
A cantilever beam has span of 3.5 m. The effective depth of beam as per deflection criteria should be:a)350b)400c)500d)700Correct answer is option 'C'. Can you explain this answer? for Civil Engineering (CE) 2025 is part of Civil Engineering (CE) preparation. The Question and answers have been prepared according to the Civil Engineering (CE) exam syllabus. Information about A cantilever beam has span of 3.5 m. The effective depth of beam as per deflection criteria should be:a)350b)400c)500d)700Correct answer is option 'C'. Can you explain this answer? covers all topics & solutions for Civil Engineering (CE) 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A cantilever beam has span of 3.5 m. The effective depth of beam as per deflection criteria should be:a)350b)400c)500d)700Correct answer is option 'C'. Can you explain this answer?.
Solutions for A cantilever beam has span of 3.5 m. The effective depth of beam as per deflection criteria should be:a)350b)400c)500d)700Correct answer is option 'C'. Can you explain this answer? in English & in Hindi are available as part of our courses for Civil Engineering (CE).
Download more important topics, notes, lectures and mock test series for Civil Engineering (CE) Exam by signing up for free.
Here you can find the meaning of A cantilever beam has span of 3.5 m. The effective depth of beam as per deflection criteria should be:a)350b)400c)500d)700Correct answer is option 'C'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A cantilever beam has span of 3.5 m. The effective depth of beam as per deflection criteria should be:a)350b)400c)500d)700Correct answer is option 'C'. Can you explain this answer?, a detailed solution for A cantilever beam has span of 3.5 m. The effective depth of beam as per deflection criteria should be:a)350b)400c)500d)700Correct answer is option 'C'. Can you explain this answer? has been provided alongside types of A cantilever beam has span of 3.5 m. The effective depth of beam as per deflection criteria should be:a)350b)400c)500d)700Correct answer is option 'C'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A cantilever beam has span of 3.5 m. The effective depth of beam as per deflection criteria should be:a)350b)400c)500d)700Correct answer is option 'C'. Can you explain this answer? tests, examples and also practice Civil Engineering (CE) tests.

|
Explore Courses for Civil Engineering (CE) exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.























