Class 12 Exam > Class 12 Questions > One face of a rectangular glass plate 6 cm th...
Start Learning for Free
One face of a rectangular glass plate 6 cm thick issilvered. An object held 8 cm in front of the firstface forms an image 12 cm behind the silveredface. The refractive index of the glass is [1996]
- a)0.4
- b)0.8
- c)1.2
- d)1.6
Correct answer is option 'C'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
One face of a rectangular glass plate 6 cm thick issilvered. An object...
Thickness of glass plate (t) = 6 cm;
Distance of the object (u) = 8 cm.
And distance of the image (v) = 12 cm.
Let x = Apparent position of the silvered
surface in cm.
Since the image is formed due to relfection at
the silvered face and by the property of mirror
image
Distance of object from the mirror = Distance
of image from the mirror
or, x + 8 = 12 + 6 – x ⇒ x = 5 cm.
Therefore, refractive index of glass
Distance of the object (u) = 8 cm.
And distance of the image (v) = 12 cm.
Let x = Apparent position of the silvered
surface in cm.
Since the image is formed due to relfection at
the silvered face and by the property of mirror
image
Distance of object from the mirror = Distance
of image from the mirror
or, x + 8 = 12 + 6 – x ⇒ x = 5 cm.
Therefore, refractive index of glass
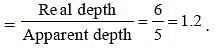
Most Upvoted Answer
One face of a rectangular glass plate 6 cm thick issilvered. An object...
The given problem involves a rectangular glass plate that is 6 cm thick and has one face that is silvered. An object is placed 8 cm in front of the silvered face, and the problem asks us to determine the refractive index of the glass.
To solve this problem, we will use the lens formula:
$\frac{1}{v} - \frac{1}{u} = \frac{1}{f}$
where:
v = image distance
u = object distance
f = focal length
We are given that the object is held 8 cm in front of the first face, so u = -8 cm (negative sign indicates that the object is on the same side as the incident light). We are also given that the image is formed 12 cm behind the silvered face, so v = -12 cm.
Now, let's consider the thickness of the glass plate. The light first enters the glass plate, then reflects off the silvered face, and finally exits the glass plate. This means that the light undergoes refraction twice, once when entering and once when exiting the glass.
Let's assume the refractive index of the glass is n. The refractive index of air is approximately 1. Therefore, when light enters the glass, it bends towards the normal. The angle of incidence is equal to the angle of refraction, so we can write:
$\sin i = n \sin r$
where i is the angle of incidence and r is the angle of refraction.
Similarly, when the light exits the glass, it bends away from the normal. Again, the angle of incidence is equal to the angle of refraction, so we can write:
$\sin i' = \frac{1}{n} \sin r'$
where i' is the angle of incidence and r' is the angle of refraction.
Since the angles of incidence and refraction are small, we can use the small angle approximation:
$\sin \theta \approx \theta$
Using this approximation, we can rewrite the equations as:
$i \approx n r$
$i' \approx \frac{r'}{n}$
Now, let's consider the geometry of the problem. The thickness of the glass plate is given as 6 cm, and the light travels a distance of 12 cm within the glass. Since the refractive index is defined as the ratio of the speed of light in vacuum to the speed of light in the medium, we can write:
$n = \frac{c}{v_g}$
where c is the speed of light in vacuum and $v_g$ is the speed of light in the glass.
The time taken by light to travel a distance d is given by:
$t = \frac{d}{v}$
The speed of light is the distance traveled per unit time, so we can write:
$v = \frac{d}{t}$
Substituting the values of d = 12 cm and t = 6 cm into the equation, we get:
$v_g = \frac{12 \ cm}{6 \ cm} = 2$
Substituting the value of $v_g$ into the equation for refractive index, we get:
$n = \frac{c}{2}$
The speed of light in vacuum is approximately $3 \times 10^8 \ m/s$, so we can write:
$n = \frac{3 \times 10^
To solve this problem, we will use the lens formula:
$\frac{1}{v} - \frac{1}{u} = \frac{1}{f}$
where:
v = image distance
u = object distance
f = focal length
We are given that the object is held 8 cm in front of the first face, so u = -8 cm (negative sign indicates that the object is on the same side as the incident light). We are also given that the image is formed 12 cm behind the silvered face, so v = -12 cm.
Now, let's consider the thickness of the glass plate. The light first enters the glass plate, then reflects off the silvered face, and finally exits the glass plate. This means that the light undergoes refraction twice, once when entering and once when exiting the glass.
Let's assume the refractive index of the glass is n. The refractive index of air is approximately 1. Therefore, when light enters the glass, it bends towards the normal. The angle of incidence is equal to the angle of refraction, so we can write:
$\sin i = n \sin r$
where i is the angle of incidence and r is the angle of refraction.
Similarly, when the light exits the glass, it bends away from the normal. Again, the angle of incidence is equal to the angle of refraction, so we can write:
$\sin i' = \frac{1}{n} \sin r'$
where i' is the angle of incidence and r' is the angle of refraction.
Since the angles of incidence and refraction are small, we can use the small angle approximation:
$\sin \theta \approx \theta$
Using this approximation, we can rewrite the equations as:
$i \approx n r$
$i' \approx \frac{r'}{n}$
Now, let's consider the geometry of the problem. The thickness of the glass plate is given as 6 cm, and the light travels a distance of 12 cm within the glass. Since the refractive index is defined as the ratio of the speed of light in vacuum to the speed of light in the medium, we can write:
$n = \frac{c}{v_g}$
where c is the speed of light in vacuum and $v_g$ is the speed of light in the glass.
The time taken by light to travel a distance d is given by:
$t = \frac{d}{v}$
The speed of light is the distance traveled per unit time, so we can write:
$v = \frac{d}{t}$
Substituting the values of d = 12 cm and t = 6 cm into the equation, we get:
$v_g = \frac{12 \ cm}{6 \ cm} = 2$
Substituting the value of $v_g$ into the equation for refractive index, we get:
$n = \frac{c}{2}$
The speed of light in vacuum is approximately $3 \times 10^8 \ m/s$, so we can write:
$n = \frac{3 \times 10^

|
Explore Courses for Class 12 exam
|

|
Similar Class 12 Doubts
One face of a rectangular glass plate 6 cm thick issilvered. An object held 8 cm in front of the firstface forms an image 12 cm behind the silveredface. The refractive index of the glass is [1996]a)0.4b)0.8c)1.2d)1.6Correct answer is option 'C'. Can you explain this answer?
Question Description
One face of a rectangular glass plate 6 cm thick issilvered. An object held 8 cm in front of the firstface forms an image 12 cm behind the silveredface. The refractive index of the glass is [1996]a)0.4b)0.8c)1.2d)1.6Correct answer is option 'C'. Can you explain this answer? for Class 12 2024 is part of Class 12 preparation. The Question and answers have been prepared according to the Class 12 exam syllabus. Information about One face of a rectangular glass plate 6 cm thick issilvered. An object held 8 cm in front of the firstface forms an image 12 cm behind the silveredface. The refractive index of the glass is [1996]a)0.4b)0.8c)1.2d)1.6Correct answer is option 'C'. Can you explain this answer? covers all topics & solutions for Class 12 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for One face of a rectangular glass plate 6 cm thick issilvered. An object held 8 cm in front of the firstface forms an image 12 cm behind the silveredface. The refractive index of the glass is [1996]a)0.4b)0.8c)1.2d)1.6Correct answer is option 'C'. Can you explain this answer?.
One face of a rectangular glass plate 6 cm thick issilvered. An object held 8 cm in front of the firstface forms an image 12 cm behind the silveredface. The refractive index of the glass is [1996]a)0.4b)0.8c)1.2d)1.6Correct answer is option 'C'. Can you explain this answer? for Class 12 2024 is part of Class 12 preparation. The Question and answers have been prepared according to the Class 12 exam syllabus. Information about One face of a rectangular glass plate 6 cm thick issilvered. An object held 8 cm in front of the firstface forms an image 12 cm behind the silveredface. The refractive index of the glass is [1996]a)0.4b)0.8c)1.2d)1.6Correct answer is option 'C'. Can you explain this answer? covers all topics & solutions for Class 12 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for One face of a rectangular glass plate 6 cm thick issilvered. An object held 8 cm in front of the firstface forms an image 12 cm behind the silveredface. The refractive index of the glass is [1996]a)0.4b)0.8c)1.2d)1.6Correct answer is option 'C'. Can you explain this answer?.
Solutions for One face of a rectangular glass plate 6 cm thick issilvered. An object held 8 cm in front of the firstface forms an image 12 cm behind the silveredface. The refractive index of the glass is [1996]a)0.4b)0.8c)1.2d)1.6Correct answer is option 'C'. Can you explain this answer? in English & in Hindi are available as part of our courses for Class 12.
Download more important topics, notes, lectures and mock test series for Class 12 Exam by signing up for free.
Here you can find the meaning of One face of a rectangular glass plate 6 cm thick issilvered. An object held 8 cm in front of the firstface forms an image 12 cm behind the silveredface. The refractive index of the glass is [1996]a)0.4b)0.8c)1.2d)1.6Correct answer is option 'C'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
One face of a rectangular glass plate 6 cm thick issilvered. An object held 8 cm in front of the firstface forms an image 12 cm behind the silveredface. The refractive index of the glass is [1996]a)0.4b)0.8c)1.2d)1.6Correct answer is option 'C'. Can you explain this answer?, a detailed solution for One face of a rectangular glass plate 6 cm thick issilvered. An object held 8 cm in front of the firstface forms an image 12 cm behind the silveredface. The refractive index of the glass is [1996]a)0.4b)0.8c)1.2d)1.6Correct answer is option 'C'. Can you explain this answer? has been provided alongside types of One face of a rectangular glass plate 6 cm thick issilvered. An object held 8 cm in front of the firstface forms an image 12 cm behind the silveredface. The refractive index of the glass is [1996]a)0.4b)0.8c)1.2d)1.6Correct answer is option 'C'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice One face of a rectangular glass plate 6 cm thick issilvered. An object held 8 cm in front of the firstface forms an image 12 cm behind the silveredface. The refractive index of the glass is [1996]a)0.4b)0.8c)1.2d)1.6Correct answer is option 'C'. Can you explain this answer? tests, examples and also practice Class 12 tests.

|
Explore Courses for Class 12 exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















