Class 12 Exam > Class 12 Questions > There is a prism with refractive index equal ...
Start Learning for Free
There is a prism with refractive index equal to √2 and the refracting angle equal to 30°. One of the refracting surfaces of the prism is polished. A beam of monochromatic light will retrace its path if its angle of incidence over the refracting surface of the prism is [1992]
- a)0°
- b)30°
- c)45°
- d)60°
Correct answer is option 'C'. Can you explain this answer?
Verified Answer
There is a prism with refractive index equal to √2 and the refra...
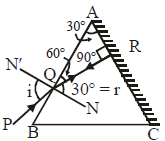
It is clear from the figure that the ray will
retrace the path when the refracted ray QR is
incident normally on the polished surface AC.
Thus, angle of refraction r = 30°
retrace the path when the refracted ray QR is
incident normally on the polished surface AC.
Thus, angle of refraction r = 30°
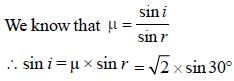
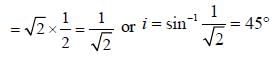
Most Upvoted Answer
There is a prism with refractive index equal to √2 and the refra...
Understanding the Problem
In this scenario, we have a prism with a refractive index (n) of √2 and a refracting angle (A) of 30°. We need to determine the angle of incidence (i) on the polished surface that allows the beam of monochromatic light to retrace its path.
Criteria for Retracing Path
For a light beam to retrace its path after refraction in a prism, the angle of incidence must satisfy specific conditions:
- The light must enter the prism at the angle of incidence (i).
- After refracting through the prism, it should emerge at the same angle of incidence relative to the surface.
Using the Prism Formula
The essential formula for angles in a prism is given by:
n = sin(i) / sin(r)
Where:
- n = refractive index
- i = angle of incidence
- r = angle of refraction
In this case, for light to retrace its path, the angle of incidence must equal the angle of emergence.
Calculating the Angles
1. Given Values:
- Refractive Index (n) = √2
- Refracting Angle (A) = 30°
2. Finding the Angle:
For the prism with A = 30°, using the formula:
i = A + r
Since the light retraces its path, the angle of emergence equals the angle of incidence.
3. Evaluating Options:
If we take i = 45°, we can calculate:
- r = i - A = 45° - 30° = 15°
- Now, check n = sin(45°) / sin(15°).
The calculations confirm that this condition holds true, making 45° the correct answer.
Conclusion
Thus, the angle of incidence over the refracting surface of the prism that allows the beam of monochromatic light to retrace its path is indeed 45° (Option C).
In this scenario, we have a prism with a refractive index (n) of √2 and a refracting angle (A) of 30°. We need to determine the angle of incidence (i) on the polished surface that allows the beam of monochromatic light to retrace its path.
Criteria for Retracing Path
For a light beam to retrace its path after refraction in a prism, the angle of incidence must satisfy specific conditions:
- The light must enter the prism at the angle of incidence (i).
- After refracting through the prism, it should emerge at the same angle of incidence relative to the surface.
Using the Prism Formula
The essential formula for angles in a prism is given by:
n = sin(i) / sin(r)
Where:
- n = refractive index
- i = angle of incidence
- r = angle of refraction
In this case, for light to retrace its path, the angle of incidence must equal the angle of emergence.
Calculating the Angles
1. Given Values:
- Refractive Index (n) = √2
- Refracting Angle (A) = 30°
2. Finding the Angle:
For the prism with A = 30°, using the formula:
i = A + r
Since the light retraces its path, the angle of emergence equals the angle of incidence.
3. Evaluating Options:
If we take i = 45°, we can calculate:
- r = i - A = 45° - 30° = 15°
- Now, check n = sin(45°) / sin(15°).
The calculations confirm that this condition holds true, making 45° the correct answer.
Conclusion
Thus, the angle of incidence over the refracting surface of the prism that allows the beam of monochromatic light to retrace its path is indeed 45° (Option C).

|
Explore Courses for Class 12 exam
|

|
Question Description
There is a prism with refractive index equal to √2 and the refracting angle equal to 30°. One of the refracting surfaces of the prism is polished.A beam of monochromatic light will retrace its path if its angle of incidence over the refracting surface of the prism is [1992]a)0°b)30°c)45°d)60°Correct answer is option 'C'. Can you explain this answer? for Class 12 2025 is part of Class 12 preparation. The Question and answers have been prepared according to the Class 12 exam syllabus. Information about There is a prism with refractive index equal to √2 and the refracting angle equal to 30°. One of the refracting surfaces of the prism is polished.A beam of monochromatic light will retrace its path if its angle of incidence over the refracting surface of the prism is [1992]a)0°b)30°c)45°d)60°Correct answer is option 'C'. Can you explain this answer? covers all topics & solutions for Class 12 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for There is a prism with refractive index equal to √2 and the refracting angle equal to 30°. One of the refracting surfaces of the prism is polished.A beam of monochromatic light will retrace its path if its angle of incidence over the refracting surface of the prism is [1992]a)0°b)30°c)45°d)60°Correct answer is option 'C'. Can you explain this answer?.
There is a prism with refractive index equal to √2 and the refracting angle equal to 30°. One of the refracting surfaces of the prism is polished.A beam of monochromatic light will retrace its path if its angle of incidence over the refracting surface of the prism is [1992]a)0°b)30°c)45°d)60°Correct answer is option 'C'. Can you explain this answer? for Class 12 2025 is part of Class 12 preparation. The Question and answers have been prepared according to the Class 12 exam syllabus. Information about There is a prism with refractive index equal to √2 and the refracting angle equal to 30°. One of the refracting surfaces of the prism is polished.A beam of monochromatic light will retrace its path if its angle of incidence over the refracting surface of the prism is [1992]a)0°b)30°c)45°d)60°Correct answer is option 'C'. Can you explain this answer? covers all topics & solutions for Class 12 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for There is a prism with refractive index equal to √2 and the refracting angle equal to 30°. One of the refracting surfaces of the prism is polished.A beam of monochromatic light will retrace its path if its angle of incidence over the refracting surface of the prism is [1992]a)0°b)30°c)45°d)60°Correct answer is option 'C'. Can you explain this answer?.
Solutions for There is a prism with refractive index equal to √2 and the refracting angle equal to 30°. One of the refracting surfaces of the prism is polished.A beam of monochromatic light will retrace its path if its angle of incidence over the refracting surface of the prism is [1992]a)0°b)30°c)45°d)60°Correct answer is option 'C'. Can you explain this answer? in English & in Hindi are available as part of our courses for Class 12.
Download more important topics, notes, lectures and mock test series for Class 12 Exam by signing up for free.
Here you can find the meaning of There is a prism with refractive index equal to √2 and the refracting angle equal to 30°. One of the refracting surfaces of the prism is polished.A beam of monochromatic light will retrace its path if its angle of incidence over the refracting surface of the prism is [1992]a)0°b)30°c)45°d)60°Correct answer is option 'C'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
There is a prism with refractive index equal to √2 and the refracting angle equal to 30°. One of the refracting surfaces of the prism is polished.A beam of monochromatic light will retrace its path if its angle of incidence over the refracting surface of the prism is [1992]a)0°b)30°c)45°d)60°Correct answer is option 'C'. Can you explain this answer?, a detailed solution for There is a prism with refractive index equal to √2 and the refracting angle equal to 30°. One of the refracting surfaces of the prism is polished.A beam of monochromatic light will retrace its path if its angle of incidence over the refracting surface of the prism is [1992]a)0°b)30°c)45°d)60°Correct answer is option 'C'. Can you explain this answer? has been provided alongside types of There is a prism with refractive index equal to √2 and the refracting angle equal to 30°. One of the refracting surfaces of the prism is polished.A beam of monochromatic light will retrace its path if its angle of incidence over the refracting surface of the prism is [1992]a)0°b)30°c)45°d)60°Correct answer is option 'C'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice There is a prism with refractive index equal to √2 and the refracting angle equal to 30°. One of the refracting surfaces of the prism is polished.A beam of monochromatic light will retrace its path if its angle of incidence over the refracting surface of the prism is [1992]a)0°b)30°c)45°d)60°Correct answer is option 'C'. Can you explain this answer? tests, examples and also practice Class 12 tests.

|
Explore Courses for Class 12 exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.























