Class 11 Exam > Class 11 Questions > A particle is moving on a circular path of ra...
Start Learning for Free
A particle is moving on a circular path of radius 1 metre with 2 metre per second if speed start increasing at a rate of 2 metre per second square then acceleration of particle is?
Verified Answer
A particle is moving on a circular path of radius 1 metre with 2 metre...
The acceleration has two components tangential acceleration and centripetal acceleration.
Tangential acceleration at = 2m/s2
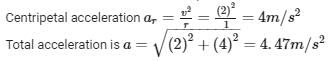
 This question is part of UPSC exam. View all Class 11 courses
This question is part of UPSC exam. View all Class 11 courses
Most Upvoted Answer
A particle is moving on a circular path of radius 1 metre with 2 metre...
Acceleration of a particle moving on a circular path can be calculated using the formula:
\[a = \frac{{v^2}}{{r}}\]
where:
- \(a\) is the acceleration of the particle,
- \(v\) is the speed of the particle, and
- \(r\) is the radius of the circular path.
In this case, the speed of the particle is increasing at a rate of 2 meters per second squared. Therefore, we need to find the acceleration of the particle when its speed is 2 meters per second.
1. Finding the initial speed:
Given that the speed of the particle is 2 meters per second, we can conclude that the initial speed is also 2 meters per second.
2. Calculating the acceleration:
Using the formula for acceleration, we substitute the known values:
\[a = \frac{{(2 \, \text{m/s})^2}}{{1 \, \text{m}}} = \frac{{4 \, \text{m}^2/\text{s}^2}}{{1 \, \text{m}}} = 4 \, \text{m/s}^2\]
Therefore, the acceleration of the particle is 4 meters per second squared.
Explanation:
When a particle moves in a circular path, it experiences centripetal acceleration directed towards the center of the circle. This acceleration is perpendicular to the velocity vector at any point on the circular path and has a magnitude given by the formula mentioned above.
In this case, as the particle's speed is increasing, it means that there must be an additional force acting on the particle, causing its acceleration. This force is called tangential force, and it is responsible for the increase in speed.
The acceleration of the particle is directly proportional to the square of its speed, as shown in the formula. This is because the greater the speed, the larger the centripetal force required to keep the particle moving in a circular path of the same radius.
In summary, the particle will experience an acceleration of 4 meters per second squared as its speed increases at a rate of 2 meters per second squared.
\[a = \frac{{v^2}}{{r}}\]
where:
- \(a\) is the acceleration of the particle,
- \(v\) is the speed of the particle, and
- \(r\) is the radius of the circular path.
In this case, the speed of the particle is increasing at a rate of 2 meters per second squared. Therefore, we need to find the acceleration of the particle when its speed is 2 meters per second.
1. Finding the initial speed:
Given that the speed of the particle is 2 meters per second, we can conclude that the initial speed is also 2 meters per second.
2. Calculating the acceleration:
Using the formula for acceleration, we substitute the known values:
\[a = \frac{{(2 \, \text{m/s})^2}}{{1 \, \text{m}}} = \frac{{4 \, \text{m}^2/\text{s}^2}}{{1 \, \text{m}}} = 4 \, \text{m/s}^2\]
Therefore, the acceleration of the particle is 4 meters per second squared.
Explanation:
When a particle moves in a circular path, it experiences centripetal acceleration directed towards the center of the circle. This acceleration is perpendicular to the velocity vector at any point on the circular path and has a magnitude given by the formula mentioned above.
In this case, as the particle's speed is increasing, it means that there must be an additional force acting on the particle, causing its acceleration. This force is called tangential force, and it is responsible for the increase in speed.
The acceleration of the particle is directly proportional to the square of its speed, as shown in the formula. This is because the greater the speed, the larger the centripetal force required to keep the particle moving in a circular path of the same radius.
In summary, the particle will experience an acceleration of 4 meters per second squared as its speed increases at a rate of 2 meters per second squared.

|
Explore Courses for Class 11 exam
|

|
Similar Class 11 Doubts
Question Description
A particle is moving on a circular path of radius 1 metre with 2 metre per second if speed start increasing at a rate of 2 metre per second square then acceleration of particle is? for Class 11 2025 is part of Class 11 preparation. The Question and answers have been prepared according to the Class 11 exam syllabus. Information about A particle is moving on a circular path of radius 1 metre with 2 metre per second if speed start increasing at a rate of 2 metre per second square then acceleration of particle is? covers all topics & solutions for Class 11 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A particle is moving on a circular path of radius 1 metre with 2 metre per second if speed start increasing at a rate of 2 metre per second square then acceleration of particle is?.
A particle is moving on a circular path of radius 1 metre with 2 metre per second if speed start increasing at a rate of 2 metre per second square then acceleration of particle is? for Class 11 2025 is part of Class 11 preparation. The Question and answers have been prepared according to the Class 11 exam syllabus. Information about A particle is moving on a circular path of radius 1 metre with 2 metre per second if speed start increasing at a rate of 2 metre per second square then acceleration of particle is? covers all topics & solutions for Class 11 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A particle is moving on a circular path of radius 1 metre with 2 metre per second if speed start increasing at a rate of 2 metre per second square then acceleration of particle is?.
Solutions for A particle is moving on a circular path of radius 1 metre with 2 metre per second if speed start increasing at a rate of 2 metre per second square then acceleration of particle is? in English & in Hindi are available as part of our courses for Class 11.
Download more important topics, notes, lectures and mock test series for Class 11 Exam by signing up for free.
Here you can find the meaning of A particle is moving on a circular path of radius 1 metre with 2 metre per second if speed start increasing at a rate of 2 metre per second square then acceleration of particle is? defined & explained in the simplest way possible. Besides giving the explanation of
A particle is moving on a circular path of radius 1 metre with 2 metre per second if speed start increasing at a rate of 2 metre per second square then acceleration of particle is?, a detailed solution for A particle is moving on a circular path of radius 1 metre with 2 metre per second if speed start increasing at a rate of 2 metre per second square then acceleration of particle is? has been provided alongside types of A particle is moving on a circular path of radius 1 metre with 2 metre per second if speed start increasing at a rate of 2 metre per second square then acceleration of particle is? theory, EduRev gives you an
ample number of questions to practice A particle is moving on a circular path of radius 1 metre with 2 metre per second if speed start increasing at a rate of 2 metre per second square then acceleration of particle is? tests, examples and also practice Class 11 tests.

|
Explore Courses for Class 11 exam
|

|
Signup to solve all Doubts
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.



























