NEET Exam > NEET Questions > If the system shown released from rest. find ...
Start Learning for Free
If the system shown released from rest. find the net work done by tension in the first one second .(g =10m/s)?
Most Upvoted Answer
If the system shown released from rest. find the net work done by tens...
**Introduction**
In order to find the net work done by tension in the first one second, we need to analyze the given system and understand the forces acting on it. By applying the principles of Newton's laws of motion and work-energy theorem, we can calculate the net work done.
**Given Information**
- The system is released from rest.
- The acceleration due to gravity, g, is given as 10 m/s².
**Analysis**
To determine the net work done by tension, we need to consider the forces acting on the system and the displacement it undergoes in the first one second.
1. **Forces Acting on the System:**
- Tension Force: The mass m₁ is connected to the pulley by a string, and the tension force acts on mass m₁.
- Weight of m₁: The mass m₁ experiences a gravitational force, which is equal to m₁ * g (where g is the acceleration due to gravity).
- Weight of m₂: The mass m₂ experiences a gravitational force, which is equal to m₂ * g.
- Normal Force: The surface on which the system rests exerts a normal force on mass m₂, equal in magnitude and opposite in direction to the weight of m₂.
2. **Displacement in the First One Second:**
- The system is released from rest, so the initial velocity is zero.
- The acceleration of the system can be determined using Newton's second law: F = m * a, where F is the net force acting on the system and m is the total mass of the system (m = m₁ + m₂).
- The acceleration can be calculated as a = (m₁ * g - m₂ * g) / m.
3. **Calculating the Net Work Done:**
- The net work done by tension in the first one second can be calculated using the work-energy theorem: W_net = ΔKE, where W_net is the net work done and ΔKE is the change in kinetic energy of the system.
- The change in kinetic energy can be calculated as ΔKE = KE_f - KE_i, where KE_f is the final kinetic energy and KE_i is the initial kinetic energy.
- As the system is released from rest, the initial kinetic energy is zero.
- The final kinetic energy can be determined using the equation KE_f = 0.5 * m * v², where m is the total mass of the system and v is the final velocity.
- The final velocity can be calculated using v = u + a * t, where u is the initial velocity (zero), a is the acceleration, and t is the time interval (one second).
4. **Calculating the Net Work Done by Tension:**
- Substitute the values of m₁, m₂, g, and t into the equations to calculate the acceleration and final velocity.
- Calculate the final kinetic energy using KE_f = 0.5 * m * v².
- Calculate the net work done by tension using W_net = ΔKE.
**Conclusion**
By following the steps outlined above, you can calculate the net work done by tension in the first one second for the given system. Make sure to substitute the given values correctly and double-check your calculations to obtain accurate results.
In order to find the net work done by tension in the first one second, we need to analyze the given system and understand the forces acting on it. By applying the principles of Newton's laws of motion and work-energy theorem, we can calculate the net work done.
**Given Information**
- The system is released from rest.
- The acceleration due to gravity, g, is given as 10 m/s².
**Analysis**
To determine the net work done by tension, we need to consider the forces acting on the system and the displacement it undergoes in the first one second.
1. **Forces Acting on the System:**
- Tension Force: The mass m₁ is connected to the pulley by a string, and the tension force acts on mass m₁.
- Weight of m₁: The mass m₁ experiences a gravitational force, which is equal to m₁ * g (where g is the acceleration due to gravity).
- Weight of m₂: The mass m₂ experiences a gravitational force, which is equal to m₂ * g.
- Normal Force: The surface on which the system rests exerts a normal force on mass m₂, equal in magnitude and opposite in direction to the weight of m₂.
2. **Displacement in the First One Second:**
- The system is released from rest, so the initial velocity is zero.
- The acceleration of the system can be determined using Newton's second law: F = m * a, where F is the net force acting on the system and m is the total mass of the system (m = m₁ + m₂).
- The acceleration can be calculated as a = (m₁ * g - m₂ * g) / m.
3. **Calculating the Net Work Done:**
- The net work done by tension in the first one second can be calculated using the work-energy theorem: W_net = ΔKE, where W_net is the net work done and ΔKE is the change in kinetic energy of the system.
- The change in kinetic energy can be calculated as ΔKE = KE_f - KE_i, where KE_f is the final kinetic energy and KE_i is the initial kinetic energy.
- As the system is released from rest, the initial kinetic energy is zero.
- The final kinetic energy can be determined using the equation KE_f = 0.5 * m * v², where m is the total mass of the system and v is the final velocity.
- The final velocity can be calculated using v = u + a * t, where u is the initial velocity (zero), a is the acceleration, and t is the time interval (one second).
4. **Calculating the Net Work Done by Tension:**
- Substitute the values of m₁, m₂, g, and t into the equations to calculate the acceleration and final velocity.
- Calculate the final kinetic energy using KE_f = 0.5 * m * v².
- Calculate the net work done by tension using W_net = ΔKE.
**Conclusion**
By following the steps outlined above, you can calculate the net work done by tension in the first one second for the given system. Make sure to substitute the given values correctly and double-check your calculations to obtain accurate results.
Community Answer
If the system shown released from rest. find the net work done by tens...
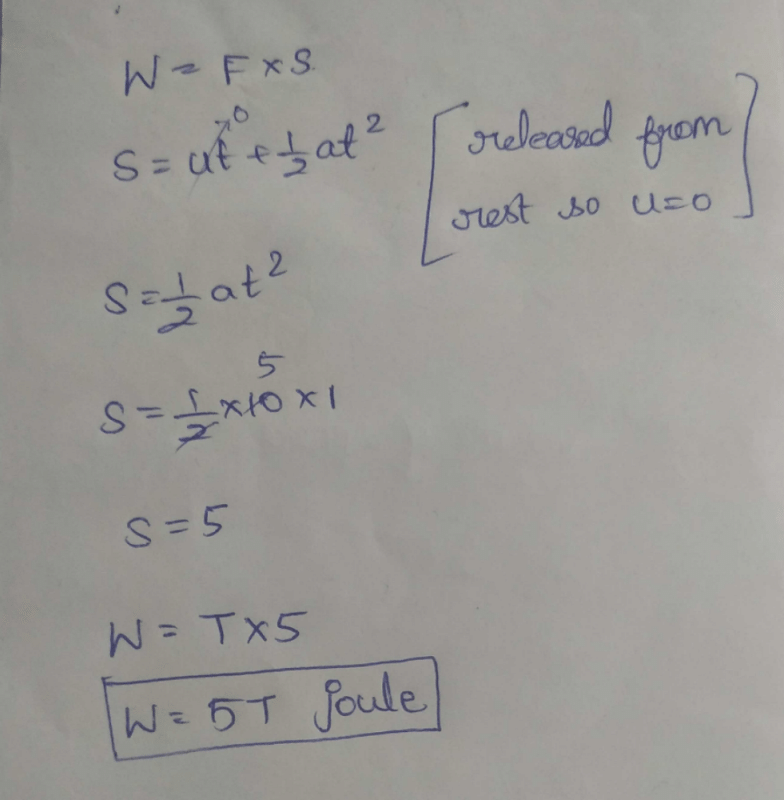

|
Explore Courses for NEET exam
|

|
Question Description
If the system shown released from rest. find the net work done by tension in the first one second .(g =10m/s)? for NEET 2025 is part of NEET preparation. The Question and answers have been prepared according to the NEET exam syllabus. Information about If the system shown released from rest. find the net work done by tension in the first one second .(g =10m/s)? covers all topics & solutions for NEET 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for If the system shown released from rest. find the net work done by tension in the first one second .(g =10m/s)?.
If the system shown released from rest. find the net work done by tension in the first one second .(g =10m/s)? for NEET 2025 is part of NEET preparation. The Question and answers have been prepared according to the NEET exam syllabus. Information about If the system shown released from rest. find the net work done by tension in the first one second .(g =10m/s)? covers all topics & solutions for NEET 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for If the system shown released from rest. find the net work done by tension in the first one second .(g =10m/s)?.
Solutions for If the system shown released from rest. find the net work done by tension in the first one second .(g =10m/s)? in English & in Hindi are available as part of our courses for NEET.
Download more important topics, notes, lectures and mock test series for NEET Exam by signing up for free.
Here you can find the meaning of If the system shown released from rest. find the net work done by tension in the first one second .(g =10m/s)? defined & explained in the simplest way possible. Besides giving the explanation of
If the system shown released from rest. find the net work done by tension in the first one second .(g =10m/s)?, a detailed solution for If the system shown released from rest. find the net work done by tension in the first one second .(g =10m/s)? has been provided alongside types of If the system shown released from rest. find the net work done by tension in the first one second .(g =10m/s)? theory, EduRev gives you an
ample number of questions to practice If the system shown released from rest. find the net work done by tension in the first one second .(g =10m/s)? tests, examples and also practice NEET tests.

|
Explore Courses for NEET exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















