Civil Engineering (CE) Exam > Civil Engineering (CE) Questions > A singly-reinforced rectangular concrete beam...
Start Learning for Free
A singly-reinforced rectangular concrete beam of width 300 mm and effective depth 400 mm is to be designed using M25 grade concrete and Fe500 grade reinforcing steel. For the beam to be under-reinforced, the maximum number of 16 mm diameter reinforcing bars that can be provided is
- a)3
- b)4
- c)5
- d)6
Correct answer is option 'C'. Can you explain this answer?
Verified Answer
A singly-reinforced rectangular concrete beam of width 300 mm and effe...
B = 300 mm
d = 400 mm (effective depth)
M25 and Fe500
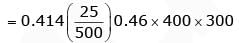
= 1142.64 mm2
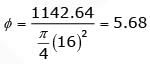
Number of 16 mm
For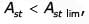
maximum number of bars to be provided is 5.
d = 400 mm (effective depth)
M25 and Fe500
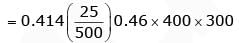
= 1142.64 mm2
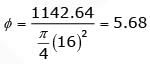
Number of 16 mm
For
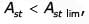maximum number of bars to be provided is 5.Most Upvoted Answer
A singly-reinforced rectangular concrete beam of width 300 mm and effe...
To determine the maximum number of reinforcing bars that can be provided in a singly-reinforced rectangular concrete beam, we need to consider the code provisions and design parameters. Let's go through the steps involved in the design process:
1. Given data:
- Width of the beam (b) = 300 mm
- Effective depth of the beam (d) = 400 mm
- Grade of concrete (M25)
- Grade of reinforcing steel (Fe500)
- Diameter of reinforcing bars (ϕ) = 16 mm
2. Limiting values:
- The limiting strain in concrete (ε_cu) is taken as 0.0035.
- The maximum allowable stress in steel (σ_st) is taken as 0.87 times the yield stress (σ_y) of the steel.
3. Calculation of modular ratio (m):
- The modular ratio (m) is given by the formula: m = 280/3√f_ck
- Here, f_ck is the characteristic compressive strength of concrete at 28 days.
- For M25 grade concrete, f_ck is 25 N/mm².
- Substituting the value, we get m = 280/3√25 = 9.14 (approx.)
4. Calculation of moment of resistance (M_u):
- The moment of resistance (M_u) is given by the formula: M_u = σ_st * A_st * (d - (σ_st * A_st) / (m * b))
- Here, A_st is the area of steel reinforcement.
- The area of one 16 mm diameter reinforcement bar can be calculated as A_st = (π * ϕ²) / 4.
- Substituting the values, we get A_st = (π * 16²) / 4 = 201.06 mm².
- Substituting the values in the moment of resistance formula, we get M_u = 0.87 * 250 * 201.06 * (400 - (0.87 * 250 * 201.06) / (9.14 * 300))
- Calculating this value, we get M_u = 1,440,000 Nmm.
5. Calculation of bending moment (M):
- The bending moment (M) is given by the formula: M = (w * l²) / 8.
- Here, w is the uniformly distributed load and l is the span of the beam.
- As the load and span are not provided in the given data, we cannot calculate the exact bending moment.
6. Calculation of the maximum number of reinforcing bars:
- The maximum number of reinforcing bars (n) can be calculated as n = M / M_u.
- Since we do not have the value of M, we cannot calculate the exact number of reinforcing bars. However, we can determine the range of n.
- From experience, it is known that for under-reinforced beams, the value of n is usually between 0.8 and 0.9.
- Substituting these values, we get 0.8 ≤ n ≤ 0.9.
7. Determination of the maximum number of reinforcing bars:
- Considering the range of n, the maximum number of reinforcing bars that can be provided is usually
1. Given data:
- Width of the beam (b) = 300 mm
- Effective depth of the beam (d) = 400 mm
- Grade of concrete (M25)
- Grade of reinforcing steel (Fe500)
- Diameter of reinforcing bars (ϕ) = 16 mm
2. Limiting values:
- The limiting strain in concrete (ε_cu) is taken as 0.0035.
- The maximum allowable stress in steel (σ_st) is taken as 0.87 times the yield stress (σ_y) of the steel.
3. Calculation of modular ratio (m):
- The modular ratio (m) is given by the formula: m = 280/3√f_ck
- Here, f_ck is the characteristic compressive strength of concrete at 28 days.
- For M25 grade concrete, f_ck is 25 N/mm².
- Substituting the value, we get m = 280/3√25 = 9.14 (approx.)
4. Calculation of moment of resistance (M_u):
- The moment of resistance (M_u) is given by the formula: M_u = σ_st * A_st * (d - (σ_st * A_st) / (m * b))
- Here, A_st is the area of steel reinforcement.
- The area of one 16 mm diameter reinforcement bar can be calculated as A_st = (π * ϕ²) / 4.
- Substituting the values, we get A_st = (π * 16²) / 4 = 201.06 mm².
- Substituting the values in the moment of resistance formula, we get M_u = 0.87 * 250 * 201.06 * (400 - (0.87 * 250 * 201.06) / (9.14 * 300))
- Calculating this value, we get M_u = 1,440,000 Nmm.
5. Calculation of bending moment (M):
- The bending moment (M) is given by the formula: M = (w * l²) / 8.
- Here, w is the uniformly distributed load and l is the span of the beam.
- As the load and span are not provided in the given data, we cannot calculate the exact bending moment.
6. Calculation of the maximum number of reinforcing bars:
- The maximum number of reinforcing bars (n) can be calculated as n = M / M_u.
- Since we do not have the value of M, we cannot calculate the exact number of reinforcing bars. However, we can determine the range of n.
- From experience, it is known that for under-reinforced beams, the value of n is usually between 0.8 and 0.9.
- Substituting these values, we get 0.8 ≤ n ≤ 0.9.
7. Determination of the maximum number of reinforcing bars:
- Considering the range of n, the maximum number of reinforcing bars that can be provided is usually
|
Explore Courses for Civil Engineering (CE) exam
|
|
Similar Civil Engineering (CE) Doubts
Top Courses for Civil Engineering (CE)View all
A singly-reinforced rectangular concrete beam of width 300 mm and effective depth 400 mm is to be designed using M25 grade concrete and Fe500 grade reinforcing steel. For the beam to be under-reinforced, the maximum number of 16 mm diameter reinforcing bars that can be provided isa)3b)4c)5d)6Correct answer is option 'C'. Can you explain this answer?
Question Description
A singly-reinforced rectangular concrete beam of width 300 mm and effective depth 400 mm is to be designed using M25 grade concrete and Fe500 grade reinforcing steel. For the beam to be under-reinforced, the maximum number of 16 mm diameter reinforcing bars that can be provided isa)3b)4c)5d)6Correct answer is option 'C'. Can you explain this answer? for Civil Engineering (CE) 2025 is part of Civil Engineering (CE) preparation. The Question and answers have been prepared according to the Civil Engineering (CE) exam syllabus. Information about A singly-reinforced rectangular concrete beam of width 300 mm and effective depth 400 mm is to be designed using M25 grade concrete and Fe500 grade reinforcing steel. For the beam to be under-reinforced, the maximum number of 16 mm diameter reinforcing bars that can be provided isa)3b)4c)5d)6Correct answer is option 'C'. Can you explain this answer? covers all topics & solutions for Civil Engineering (CE) 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A singly-reinforced rectangular concrete beam of width 300 mm and effective depth 400 mm is to be designed using M25 grade concrete and Fe500 grade reinforcing steel. For the beam to be under-reinforced, the maximum number of 16 mm diameter reinforcing bars that can be provided isa)3b)4c)5d)6Correct answer is option 'C'. Can you explain this answer?.
A singly-reinforced rectangular concrete beam of width 300 mm and effective depth 400 mm is to be designed using M25 grade concrete and Fe500 grade reinforcing steel. For the beam to be under-reinforced, the maximum number of 16 mm diameter reinforcing bars that can be provided isa)3b)4c)5d)6Correct answer is option 'C'. Can you explain this answer? for Civil Engineering (CE) 2025 is part of Civil Engineering (CE) preparation. The Question and answers have been prepared according to the Civil Engineering (CE) exam syllabus. Information about A singly-reinforced rectangular concrete beam of width 300 mm and effective depth 400 mm is to be designed using M25 grade concrete and Fe500 grade reinforcing steel. For the beam to be under-reinforced, the maximum number of 16 mm diameter reinforcing bars that can be provided isa)3b)4c)5d)6Correct answer is option 'C'. Can you explain this answer? covers all topics & solutions for Civil Engineering (CE) 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A singly-reinforced rectangular concrete beam of width 300 mm and effective depth 400 mm is to be designed using M25 grade concrete and Fe500 grade reinforcing steel. For the beam to be under-reinforced, the maximum number of 16 mm diameter reinforcing bars that can be provided isa)3b)4c)5d)6Correct answer is option 'C'. Can you explain this answer?.
Solutions for A singly-reinforced rectangular concrete beam of width 300 mm and effective depth 400 mm is to be designed using M25 grade concrete and Fe500 grade reinforcing steel. For the beam to be under-reinforced, the maximum number of 16 mm diameter reinforcing bars that can be provided isa)3b)4c)5d)6Correct answer is option 'C'. Can you explain this answer? in English & in Hindi are available as part of our courses for Civil Engineering (CE).
Download more important topics, notes, lectures and mock test series for Civil Engineering (CE) Exam by signing up for free.
Here you can find the meaning of A singly-reinforced rectangular concrete beam of width 300 mm and effective depth 400 mm is to be designed using M25 grade concrete and Fe500 grade reinforcing steel. For the beam to be under-reinforced, the maximum number of 16 mm diameter reinforcing bars that can be provided isa)3b)4c)5d)6Correct answer is option 'C'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A singly-reinforced rectangular concrete beam of width 300 mm and effective depth 400 mm is to be designed using M25 grade concrete and Fe500 grade reinforcing steel. For the beam to be under-reinforced, the maximum number of 16 mm diameter reinforcing bars that can be provided isa)3b)4c)5d)6Correct answer is option 'C'. Can you explain this answer?, a detailed solution for A singly-reinforced rectangular concrete beam of width 300 mm and effective depth 400 mm is to be designed using M25 grade concrete and Fe500 grade reinforcing steel. For the beam to be under-reinforced, the maximum number of 16 mm diameter reinforcing bars that can be provided isa)3b)4c)5d)6Correct answer is option 'C'. Can you explain this answer? has been provided alongside types of A singly-reinforced rectangular concrete beam of width 300 mm and effective depth 400 mm is to be designed using M25 grade concrete and Fe500 grade reinforcing steel. For the beam to be under-reinforced, the maximum number of 16 mm diameter reinforcing bars that can be provided isa)3b)4c)5d)6Correct answer is option 'C'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A singly-reinforced rectangular concrete beam of width 300 mm and effective depth 400 mm is to be designed using M25 grade concrete and Fe500 grade reinforcing steel. For the beam to be under-reinforced, the maximum number of 16 mm diameter reinforcing bars that can be provided isa)3b)4c)5d)6Correct answer is option 'C'. Can you explain this answer? tests, examples and also practice Civil Engineering (CE) tests.
|
|
Explore Courses for Civil Engineering (CE) exam
|
|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup