Physics Exam > Physics Questions > Two space ships approach Earth with equal spe...
Start Learning for Free
Two space ships approach Earth with equal speeds as measured by an observer on Earth, but from opposite directions. A meter stick on one spaceship is measured to be 60 cm long by an occupant of the other ship. What is the speed of each spaceship as measured from earth. (in units of c)?
Correct answer is '0.5'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
Two space ships approach Earth with equal speeds as measured by an obs...
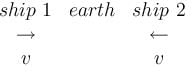
length of stick on ship 1 measured by ship 2 = 60 cm

Now, since each ship is moving with velocity v.
∴ Velocity of ship 2 wrt ship 1 = 2v

l0 = 1m (meter stick)
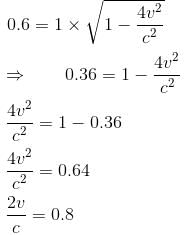
v = 0.4c
Speed of each ship = 0.4c
The correct answer is: 0.4
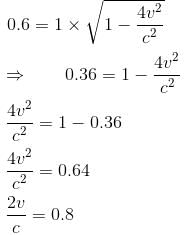
v = 0.4c
Speed of each ship = 0.4c
The correct answer is: 0.4
Most Upvoted Answer
Two space ships approach Earth with equal speeds as measured by an obs...
Given information:
- Two spaceships approach Earth with equal speeds as measured by an observer on Earth.
- The spaceships are approaching from opposite directions.
- A meter stick on one spaceship is measured to be 60 cm long by an occupant of the other ship.
To find:
The speed of each spaceship as measured from Earth.
Explanation:
To solve this problem, we need to use the concept of time dilation from special relativity. According to special relativity, time dilation occurs when an observer moves relative to another observer at a significant fraction of the speed of light.
Step 1: Establish the frame of reference:
- Let's assume that the observer on Earth is at rest and is measuring the speed of the spaceships.
- We will use the observer on Earth as our frame of reference.
Step 2: Understand the concept of time dilation:
- Time dilation occurs when an object is moving relative to an observer at a significant fraction of the speed of light.
- In this case, the spaceships are approaching Earth with equal speeds, so we can assume that they are moving at the same speed relative to Earth.
- Therefore, the time dilation effect will be the same for both spaceships.
Step 3: Apply the time dilation formula:
- The time dilation formula is given by:
Δt' = Δt / √(1 - v^2/c^2)
where:
Δt' = time measured by the moving observer
Δt = time measured by the stationary observer (on Earth)
v = relative velocity between the observer and the moving object
c = speed of light
Step 4: Use the given information to find the speed of the spaceships:
- According to the question, a meter stick on one spaceship is measured to be 60 cm long by an occupant of the other ship.
- Let's assume that the spaceship with the meter stick is spaceship A, and the other spaceship is spaceship B.
- The length contraction formula is given by:
L' = L / √(1 - v^2/c^2)
where:
L' = length measured by the moving observer
L = length measured by the stationary observer (on Earth)
v = relative velocity between the observer and the moving object
c = speed of light
- In this case, the length measured by the occupant of spaceship B (L') is 60 cm.
- The length measured by the observer on Earth (L) is the actual length of the meter stick, which is 100 cm (1 meter).
- Substituting these values into the length contraction formula, we get:
60 = 100 / √(1 - v^2/c^2)
Step 5: Solve for the speed of the spaceships:
- Rearranging the equation, we have:
√(1 - v^2/c^2) = 100/60
√(1 - v^2/c^2) = 5/3
- Squaring both sides of the equation, we get:
1 - v^2/c^2 = 25/9
- Rearranging the equation, we have:
v^2/c^2 =
- Two spaceships approach Earth with equal speeds as measured by an observer on Earth.
- The spaceships are approaching from opposite directions.
- A meter stick on one spaceship is measured to be 60 cm long by an occupant of the other ship.
To find:
The speed of each spaceship as measured from Earth.
Explanation:
To solve this problem, we need to use the concept of time dilation from special relativity. According to special relativity, time dilation occurs when an observer moves relative to another observer at a significant fraction of the speed of light.
Step 1: Establish the frame of reference:
- Let's assume that the observer on Earth is at rest and is measuring the speed of the spaceships.
- We will use the observer on Earth as our frame of reference.
Step 2: Understand the concept of time dilation:
- Time dilation occurs when an object is moving relative to an observer at a significant fraction of the speed of light.
- In this case, the spaceships are approaching Earth with equal speeds, so we can assume that they are moving at the same speed relative to Earth.
- Therefore, the time dilation effect will be the same for both spaceships.
Step 3: Apply the time dilation formula:
- The time dilation formula is given by:
Δt' = Δt / √(1 - v^2/c^2)
where:
Δt' = time measured by the moving observer
Δt = time measured by the stationary observer (on Earth)
v = relative velocity between the observer and the moving object
c = speed of light
Step 4: Use the given information to find the speed of the spaceships:
- According to the question, a meter stick on one spaceship is measured to be 60 cm long by an occupant of the other ship.
- Let's assume that the spaceship with the meter stick is spaceship A, and the other spaceship is spaceship B.
- The length contraction formula is given by:
L' = L / √(1 - v^2/c^2)
where:
L' = length measured by the moving observer
L = length measured by the stationary observer (on Earth)
v = relative velocity between the observer and the moving object
c = speed of light
- In this case, the length measured by the occupant of spaceship B (L') is 60 cm.
- The length measured by the observer on Earth (L) is the actual length of the meter stick, which is 100 cm (1 meter).
- Substituting these values into the length contraction formula, we get:
60 = 100 / √(1 - v^2/c^2)
Step 5: Solve for the speed of the spaceships:
- Rearranging the equation, we have:
√(1 - v^2/c^2) = 100/60
√(1 - v^2/c^2) = 5/3
- Squaring both sides of the equation, we get:
1 - v^2/c^2 = 25/9
- Rearranging the equation, we have:
v^2/c^2 =

|
Explore Courses for Physics exam
|

|
Similar Physics Doubts
Two space ships approach Earth with equal speeds as measured by an observer on Earth, but from opposite directions. A meter stick on one spaceship is measured to be 60cmlong by an occupant of the other ship. What is the speed of each spaceship as measured from earth. (in units ofc)?Correct answer is '0.5'. Can you explain this answer?
Question Description
Two space ships approach Earth with equal speeds as measured by an observer on Earth, but from opposite directions. A meter stick on one spaceship is measured to be 60cmlong by an occupant of the other ship. What is the speed of each spaceship as measured from earth. (in units ofc)?Correct answer is '0.5'. Can you explain this answer? for Physics 2024 is part of Physics preparation. The Question and answers have been prepared according to the Physics exam syllabus. Information about Two space ships approach Earth with equal speeds as measured by an observer on Earth, but from opposite directions. A meter stick on one spaceship is measured to be 60cmlong by an occupant of the other ship. What is the speed of each spaceship as measured from earth. (in units ofc)?Correct answer is '0.5'. Can you explain this answer? covers all topics & solutions for Physics 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Two space ships approach Earth with equal speeds as measured by an observer on Earth, but from opposite directions. A meter stick on one spaceship is measured to be 60cmlong by an occupant of the other ship. What is the speed of each spaceship as measured from earth. (in units ofc)?Correct answer is '0.5'. Can you explain this answer?.
Two space ships approach Earth with equal speeds as measured by an observer on Earth, but from opposite directions. A meter stick on one spaceship is measured to be 60cmlong by an occupant of the other ship. What is the speed of each spaceship as measured from earth. (in units ofc)?Correct answer is '0.5'. Can you explain this answer? for Physics 2024 is part of Physics preparation. The Question and answers have been prepared according to the Physics exam syllabus. Information about Two space ships approach Earth with equal speeds as measured by an observer on Earth, but from opposite directions. A meter stick on one spaceship is measured to be 60cmlong by an occupant of the other ship. What is the speed of each spaceship as measured from earth. (in units ofc)?Correct answer is '0.5'. Can you explain this answer? covers all topics & solutions for Physics 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Two space ships approach Earth with equal speeds as measured by an observer on Earth, but from opposite directions. A meter stick on one spaceship is measured to be 60cmlong by an occupant of the other ship. What is the speed of each spaceship as measured from earth. (in units ofc)?Correct answer is '0.5'. Can you explain this answer?.
Solutions for Two space ships approach Earth with equal speeds as measured by an observer on Earth, but from opposite directions. A meter stick on one spaceship is measured to be 60cmlong by an occupant of the other ship. What is the speed of each spaceship as measured from earth. (in units ofc)?Correct answer is '0.5'. Can you explain this answer? in English & in Hindi are available as part of our courses for Physics.
Download more important topics, notes, lectures and mock test series for Physics Exam by signing up for free.
Here you can find the meaning of Two space ships approach Earth with equal speeds as measured by an observer on Earth, but from opposite directions. A meter stick on one spaceship is measured to be 60cmlong by an occupant of the other ship. What is the speed of each spaceship as measured from earth. (in units ofc)?Correct answer is '0.5'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Two space ships approach Earth with equal speeds as measured by an observer on Earth, but from opposite directions. A meter stick on one spaceship is measured to be 60cmlong by an occupant of the other ship. What is the speed of each spaceship as measured from earth. (in units ofc)?Correct answer is '0.5'. Can you explain this answer?, a detailed solution for Two space ships approach Earth with equal speeds as measured by an observer on Earth, but from opposite directions. A meter stick on one spaceship is measured to be 60cmlong by an occupant of the other ship. What is the speed of each spaceship as measured from earth. (in units ofc)?Correct answer is '0.5'. Can you explain this answer? has been provided alongside types of Two space ships approach Earth with equal speeds as measured by an observer on Earth, but from opposite directions. A meter stick on one spaceship is measured to be 60cmlong by an occupant of the other ship. What is the speed of each spaceship as measured from earth. (in units ofc)?Correct answer is '0.5'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Two space ships approach Earth with equal speeds as measured by an observer on Earth, but from opposite directions. A meter stick on one spaceship is measured to be 60cmlong by an occupant of the other ship. What is the speed of each spaceship as measured from earth. (in units ofc)?Correct answer is '0.5'. Can you explain this answer? tests, examples and also practice Physics tests.

|
Explore Courses for Physics exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















