Civil Engineering (CE) Exam > Civil Engineering (CE) Questions > Sedimentation basin in a water treatment plan...
Start Learning for Free
Sedimentation basin in a water treatment plant is designed for a flow rate of 0.2 m3/s. The basin is rectangular with a length of 32m, width of 8m and depth of 4m. Assume that the settling velocity of these particles is governed by the Stokes’ law. Given: density of the particles = 2.5 g/cm3; density of water = 1 g/cm3; dynamic viscosity of water = 0.01 g/(cm.s); gravitational acceleration = 980 cm/s2. If the incoming water contains particles of diameter 25 μm (spherical and uniform) the removal efficiency of these particles is
- a)100%
- b)65%
- c)78%
- d)51%
Correct answer is option 'B'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
Sedimentation basin in a water treatment plant is designed for a flow ...
Flow rate = 0.2 m3/sec
Dimension of tank = 32m × 8 m × 4 m
Density of particles = 2.5 g/cc
Density of water = 1 g/cc
Dynamic viscosity of water = 0.01 g/cm-S
Diameter of particle = 25 μm
We know that
Over flow rate of tank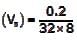
= 7.8125 × 10-4 m/sec
And settling velocity of particle (vs),
Dimension of tank = 32m × 8 m × 4 m
Density of particles = 2.5 g/cc
Density of water = 1 g/cc
Dynamic viscosity of water = 0.01 g/cm-S
Diameter of particle = 25 μm
We know that
Over flow rate of tank
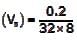
= 7.8125 × 10-4 m/sec
And settling velocity of particle (vs),
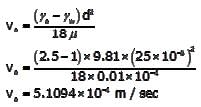
Now, % removal efficiency
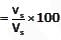
Hence option (b) is correct.
Most Upvoted Answer
Sedimentation basin in a water treatment plant is designed for a flow ...
Law and the particles have a diameter of 0.02 mm.
To calculate the settling velocity of the particles, we can use the Stokes law equation:
Vs = (2/9) * (ρp - ρw) * g * (dp^2) / η
Where:
Vs is the settling velocity of the particles,
ρp is the density of the particles,
ρw is the density of the water,
g is the acceleration due to gravity,
dp is the diameter of the particles, and
η is the dynamic viscosity of the water.
First, we need to calculate the density of the particles and the density of the water.
Given:
Density of water, ρw = 1000 kg/m^3
Diameter of particles, dp = 0.02 mm = 0.02 * 10^-3 m
Assuming the particles are spherical, we can calculate the volume and the density of the particles as follows:
Volume of particles = (4/3) * π * (dp/2)^3
Density of particles = Mass of particles / Volume of particles
The mass of the particles can be calculated using the following formula:
Mass of particles = Density of particles * Volume of particles
Now, we can substitute the values into the equations and calculate the settling velocity of the particles.
Let's assume the density of the particles is 2500 kg/m^3.
Volume of particles = (4/3) * π * (0.02/2)^3 = 8.3776 * 10^-8 m^3
Density of particles = 2500 kg/m^3
Mass of particles = 2500 kg/m^3 * 8.3776 * 10^-8 m^3 = 2.0944 * 10^-4 kg
Substituting these values into the Stokes law equation:
Vs = (2/9) * (2500 kg/m^3 - 1000 kg/m^3) * 9.81 m/s^2 * (0.02 * 10^-3 m)^2 / η
Given that the dynamic viscosity of water, η, is approximately 0.001 kg/(m·s), we can calculate the settling velocity:
Vs = (2/9) * (1500 kg/m^3) * 9.81 m/s^2 * (0.02 * 10^-3 m)^2 / 0.001 kg/(m·s)
≈ 1.7456 * 10^-6 m/s
Therefore, the settling velocity of the particles is approximately 1.7456 * 10^-6 m/s.
To determine if the sedimentation basin is suitable for the given flow rate, we need to calculate the volume of the basin and the time required for the particles to settle.
The volume of the basin can be calculated as follows:
Volume of basin = Length * Width * Depth
= 32 m * 8 m * 4 m
= 1024 m^3
To calculate the time required for the particles to settle, we can use the following equation:
Time = Volume of basin / Flow rate
Time = 1024 m^3 / 0.2 m^3/s
= 5120 s
Therefore, the sedimentation basin in the water treatment plant can hold 1024 m
To calculate the settling velocity of the particles, we can use the Stokes law equation:
Vs = (2/9) * (ρp - ρw) * g * (dp^2) / η
Where:
Vs is the settling velocity of the particles,
ρp is the density of the particles,
ρw is the density of the water,
g is the acceleration due to gravity,
dp is the diameter of the particles, and
η is the dynamic viscosity of the water.
First, we need to calculate the density of the particles and the density of the water.
Given:
Density of water, ρw = 1000 kg/m^3
Diameter of particles, dp = 0.02 mm = 0.02 * 10^-3 m
Assuming the particles are spherical, we can calculate the volume and the density of the particles as follows:
Volume of particles = (4/3) * π * (dp/2)^3
Density of particles = Mass of particles / Volume of particles
The mass of the particles can be calculated using the following formula:
Mass of particles = Density of particles * Volume of particles
Now, we can substitute the values into the equations and calculate the settling velocity of the particles.
Let's assume the density of the particles is 2500 kg/m^3.
Volume of particles = (4/3) * π * (0.02/2)^3 = 8.3776 * 10^-8 m^3
Density of particles = 2500 kg/m^3
Mass of particles = 2500 kg/m^3 * 8.3776 * 10^-8 m^3 = 2.0944 * 10^-4 kg
Substituting these values into the Stokes law equation:
Vs = (2/9) * (2500 kg/m^3 - 1000 kg/m^3) * 9.81 m/s^2 * (0.02 * 10^-3 m)^2 / η
Given that the dynamic viscosity of water, η, is approximately 0.001 kg/(m·s), we can calculate the settling velocity:
Vs = (2/9) * (1500 kg/m^3) * 9.81 m/s^2 * (0.02 * 10^-3 m)^2 / 0.001 kg/(m·s)
≈ 1.7456 * 10^-6 m/s
Therefore, the settling velocity of the particles is approximately 1.7456 * 10^-6 m/s.
To determine if the sedimentation basin is suitable for the given flow rate, we need to calculate the volume of the basin and the time required for the particles to settle.
The volume of the basin can be calculated as follows:
Volume of basin = Length * Width * Depth
= 32 m * 8 m * 4 m
= 1024 m^3
To calculate the time required for the particles to settle, we can use the following equation:
Time = Volume of basin / Flow rate
Time = 1024 m^3 / 0.2 m^3/s
= 5120 s
Therefore, the sedimentation basin in the water treatment plant can hold 1024 m
Attention Civil Engineering (CE) Students!
To make sure you are not studying endlessly, EduRev has designed Civil Engineering (CE) study material, with Structured Courses, Videos, & Test Series. Plus get personalized analysis, doubt solving and improvement plans to achieve a great score in Civil Engineering (CE).
|
Explore Courses for Civil Engineering (CE) exam
|
|
Similar Civil Engineering (CE) Doubts
Top Courses for Civil Engineering (CE)View all
Sedimentation basin in a water treatment plant is designed for a flow rate of 0.2 m3/s. The basin is rectangular with a length of 32m, width of 8m and depth of 4m. Assume that the settling velocity of these particles is governed by the Stokes’ law. Given: density of the particles = 2.5 g/cm3; density of water = 1 g/cm3; dynamic viscosity of water = 0.01 g/(cm.s); gravitational acceleration = 980 cm/s2. If the incoming water contains particles of diameter 25 μm (spherical and uniform) the removal efficiency of these particles isa)100%b)65%c)78%d)51%Correct answer is option 'B'. Can you explain this answer?
Question Description
Sedimentation basin in a water treatment plant is designed for a flow rate of 0.2 m3/s. The basin is rectangular with a length of 32m, width of 8m and depth of 4m. Assume that the settling velocity of these particles is governed by the Stokes’ law. Given: density of the particles = 2.5 g/cm3; density of water = 1 g/cm3; dynamic viscosity of water = 0.01 g/(cm.s); gravitational acceleration = 980 cm/s2. If the incoming water contains particles of diameter 25 μm (spherical and uniform) the removal efficiency of these particles isa)100%b)65%c)78%d)51%Correct answer is option 'B'. Can you explain this answer? for Civil Engineering (CE) 2024 is part of Civil Engineering (CE) preparation. The Question and answers have been prepared according to the Civil Engineering (CE) exam syllabus. Information about Sedimentation basin in a water treatment plant is designed for a flow rate of 0.2 m3/s. The basin is rectangular with a length of 32m, width of 8m and depth of 4m. Assume that the settling velocity of these particles is governed by the Stokes’ law. Given: density of the particles = 2.5 g/cm3; density of water = 1 g/cm3; dynamic viscosity of water = 0.01 g/(cm.s); gravitational acceleration = 980 cm/s2. If the incoming water contains particles of diameter 25 μm (spherical and uniform) the removal efficiency of these particles isa)100%b)65%c)78%d)51%Correct answer is option 'B'. Can you explain this answer? covers all topics & solutions for Civil Engineering (CE) 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Sedimentation basin in a water treatment plant is designed for a flow rate of 0.2 m3/s. The basin is rectangular with a length of 32m, width of 8m and depth of 4m. Assume that the settling velocity of these particles is governed by the Stokes’ law. Given: density of the particles = 2.5 g/cm3; density of water = 1 g/cm3; dynamic viscosity of water = 0.01 g/(cm.s); gravitational acceleration = 980 cm/s2. If the incoming water contains particles of diameter 25 μm (spherical and uniform) the removal efficiency of these particles isa)100%b)65%c)78%d)51%Correct answer is option 'B'. Can you explain this answer?.
Sedimentation basin in a water treatment plant is designed for a flow rate of 0.2 m3/s. The basin is rectangular with a length of 32m, width of 8m and depth of 4m. Assume that the settling velocity of these particles is governed by the Stokes’ law. Given: density of the particles = 2.5 g/cm3; density of water = 1 g/cm3; dynamic viscosity of water = 0.01 g/(cm.s); gravitational acceleration = 980 cm/s2. If the incoming water contains particles of diameter 25 μm (spherical and uniform) the removal efficiency of these particles isa)100%b)65%c)78%d)51%Correct answer is option 'B'. Can you explain this answer? for Civil Engineering (CE) 2024 is part of Civil Engineering (CE) preparation. The Question and answers have been prepared according to the Civil Engineering (CE) exam syllabus. Information about Sedimentation basin in a water treatment plant is designed for a flow rate of 0.2 m3/s. The basin is rectangular with a length of 32m, width of 8m and depth of 4m. Assume that the settling velocity of these particles is governed by the Stokes’ law. Given: density of the particles = 2.5 g/cm3; density of water = 1 g/cm3; dynamic viscosity of water = 0.01 g/(cm.s); gravitational acceleration = 980 cm/s2. If the incoming water contains particles of diameter 25 μm (spherical and uniform) the removal efficiency of these particles isa)100%b)65%c)78%d)51%Correct answer is option 'B'. Can you explain this answer? covers all topics & solutions for Civil Engineering (CE) 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Sedimentation basin in a water treatment plant is designed for a flow rate of 0.2 m3/s. The basin is rectangular with a length of 32m, width of 8m and depth of 4m. Assume that the settling velocity of these particles is governed by the Stokes’ law. Given: density of the particles = 2.5 g/cm3; density of water = 1 g/cm3; dynamic viscosity of water = 0.01 g/(cm.s); gravitational acceleration = 980 cm/s2. If the incoming water contains particles of diameter 25 μm (spherical and uniform) the removal efficiency of these particles isa)100%b)65%c)78%d)51%Correct answer is option 'B'. Can you explain this answer?.
Solutions for Sedimentation basin in a water treatment plant is designed for a flow rate of 0.2 m3/s. The basin is rectangular with a length of 32m, width of 8m and depth of 4m. Assume that the settling velocity of these particles is governed by the Stokes’ law. Given: density of the particles = 2.5 g/cm3; density of water = 1 g/cm3; dynamic viscosity of water = 0.01 g/(cm.s); gravitational acceleration = 980 cm/s2. If the incoming water contains particles of diameter 25 μm (spherical and uniform) the removal efficiency of these particles isa)100%b)65%c)78%d)51%Correct answer is option 'B'. Can you explain this answer? in English & in Hindi are available as part of our courses for Civil Engineering (CE).
Download more important topics, notes, lectures and mock test series for Civil Engineering (CE) Exam by signing up for free.
Here you can find the meaning of Sedimentation basin in a water treatment plant is designed for a flow rate of 0.2 m3/s. The basin is rectangular with a length of 32m, width of 8m and depth of 4m. Assume that the settling velocity of these particles is governed by the Stokes’ law. Given: density of the particles = 2.5 g/cm3; density of water = 1 g/cm3; dynamic viscosity of water = 0.01 g/(cm.s); gravitational acceleration = 980 cm/s2. If the incoming water contains particles of diameter 25 μm (spherical and uniform) the removal efficiency of these particles isa)100%b)65%c)78%d)51%Correct answer is option 'B'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Sedimentation basin in a water treatment plant is designed for a flow rate of 0.2 m3/s. The basin is rectangular with a length of 32m, width of 8m and depth of 4m. Assume that the settling velocity of these particles is governed by the Stokes’ law. Given: density of the particles = 2.5 g/cm3; density of water = 1 g/cm3; dynamic viscosity of water = 0.01 g/(cm.s); gravitational acceleration = 980 cm/s2. If the incoming water contains particles of diameter 25 μm (spherical and uniform) the removal efficiency of these particles isa)100%b)65%c)78%d)51%Correct answer is option 'B'. Can you explain this answer?, a detailed solution for Sedimentation basin in a water treatment plant is designed for a flow rate of 0.2 m3/s. The basin is rectangular with a length of 32m, width of 8m and depth of 4m. Assume that the settling velocity of these particles is governed by the Stokes’ law. Given: density of the particles = 2.5 g/cm3; density of water = 1 g/cm3; dynamic viscosity of water = 0.01 g/(cm.s); gravitational acceleration = 980 cm/s2. If the incoming water contains particles of diameter 25 μm (spherical and uniform) the removal efficiency of these particles isa)100%b)65%c)78%d)51%Correct answer is option 'B'. Can you explain this answer? has been provided alongside types of Sedimentation basin in a water treatment plant is designed for a flow rate of 0.2 m3/s. The basin is rectangular with a length of 32m, width of 8m and depth of 4m. Assume that the settling velocity of these particles is governed by the Stokes’ law. Given: density of the particles = 2.5 g/cm3; density of water = 1 g/cm3; dynamic viscosity of water = 0.01 g/(cm.s); gravitational acceleration = 980 cm/s2. If the incoming water contains particles of diameter 25 μm (spherical and uniform) the removal efficiency of these particles isa)100%b)65%c)78%d)51%Correct answer is option 'B'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Sedimentation basin in a water treatment plant is designed for a flow rate of 0.2 m3/s. The basin is rectangular with a length of 32m, width of 8m and depth of 4m. Assume that the settling velocity of these particles is governed by the Stokes’ law. Given: density of the particles = 2.5 g/cm3; density of water = 1 g/cm3; dynamic viscosity of water = 0.01 g/(cm.s); gravitational acceleration = 980 cm/s2. If the incoming water contains particles of diameter 25 μm (spherical and uniform) the removal efficiency of these particles isa)100%b)65%c)78%d)51%Correct answer is option 'B'. Can you explain this answer? tests, examples and also practice Civil Engineering (CE) tests.
|
|
Explore Courses for Civil Engineering (CE) exam
|
|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
|
© EduRev
|
Education Revolution
|
Follow Us
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup