JEE Exam > JEE Questions > The moment of inertia of a uniform disc about...
Start Learning for Free
The moment of inertia of a uniform disc about an axis passing through its centre and perpendicular to its plane is 1kg - m2. It is rotating with an angular velocity 100 radians/second. Another identical disc is gently placed on it so that their centres coincide. Now these two discs together continue to rotate about the same axis. Then the loss in kinetic energy in kilo joules is
- a)2.5
- b)3.0
- c)3.5
- d)4.0
Correct answer is option 'A'. Can you explain this answer?
Verified Answer
The moment of inertia of a uniform disc about an axis passing through ...
Correct answer is option 'A' : 2.5
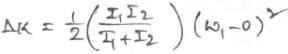
View all questions of this test
Most Upvoted Answer
The moment of inertia of a uniform disc about an axis passing through ...
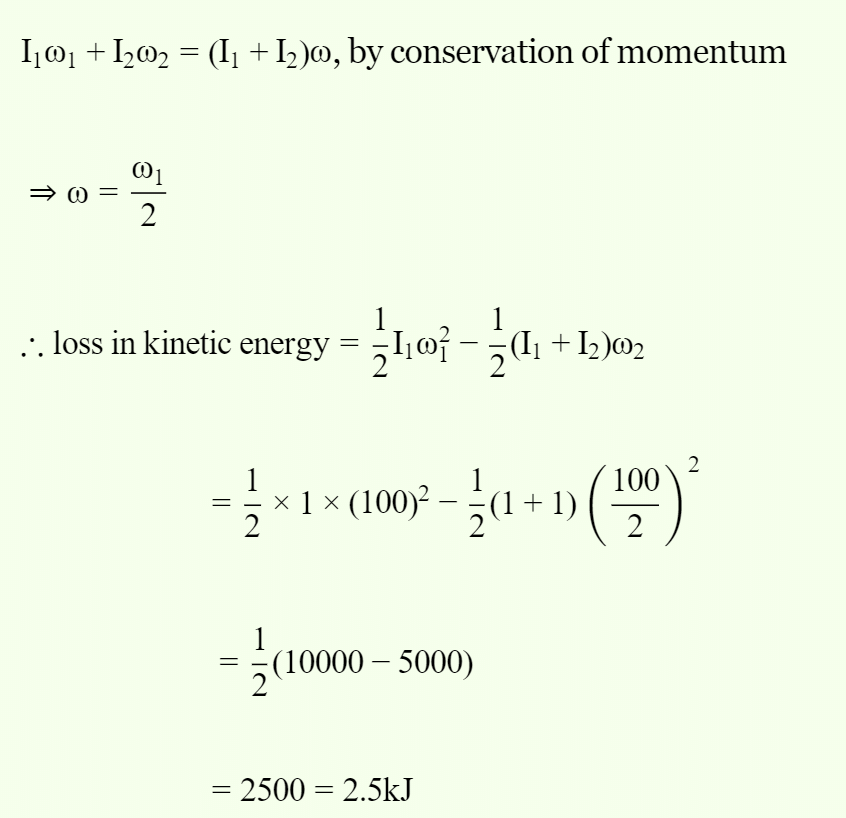
Free Test
FREE
| Start Free Test |
Community Answer
The moment of inertia of a uniform disc about an axis passing through ...
Loss in Kinetic Energy of the System
The loss in kinetic energy of the system can be calculated by considering the initial and final kinetic energy of the discs.
Initial Kinetic Energy:
The initial kinetic energy of the system is given by the sum of the kinetic energies of the individual discs. Since the discs are identical, their masses and moments of inertia are the same.
The kinetic energy of a rotating object is given by the formula:
K_initial = (1/2) I_initial ω^2
where K_initial is the initial kinetic energy, I_initial is the initial moment of inertia, and ω is the initial angular velocity.
Given that the moment of inertia of each disc is 1 kg-m^2 and the initial angular velocity is 100 radians/second, we can calculate the initial kinetic energy of each disc:
K_initial = (1/2) (1 kg-m^2) (100 radians/second)^2
= (1/2) (1 kg-m^2) (10,000 radians^2/second^2)
= 5,000 kg-m^2/s^2
Since there are two discs, the initial total kinetic energy of the system is:
K_initial_total = 2 × 5,000 kg-m^2/s^2
= 10,000 kg-m^2/s^2
Final Kinetic Energy:
When the second disc is gently placed on the first disc, the two discs start rotating together about the same axis. The final moment of inertia of the system can be obtained by considering the moment of inertia of each disc and the parallel axis theorem.
The parallel axis theorem states that the moment of inertia of an object about an axis parallel to and a distance 'd' away from the axis passing through its center is given by:
I_final = I_initial + md^2
where I_initial is the initial moment of inertia, m is the mass of the object, and d is the distance between the two axes.
Since the discs are identical and their centers coincide, the distance between the two axes is zero. Therefore, the final moment of inertia of the system remains the same as the initial moment of inertia:
I_final = I_initial
= 1 kg-m^2
The final angular velocity of the system can be calculated by applying the principle of conservation of angular momentum. Since there are no external torques acting on the system, the total angular momentum of the system remains constant.
Initial angular momentum = Final angular momentum
I_initial ω_initial = I_final ω_final
Substituting the values, we get:
(1 kg-m^2) (100 radians/second) = (1 kg-m^2) ω_final
ω_final = 100 radians/second
The final kinetic energy of the system can be calculated using the formula mentioned earlier:
K_final = (1/2) I_final ω_final^2
Substituting the values, we get:
K_final = (1/2) (1 kg-m^2) (100 radians/second)^2
= (1/2) (1 kg-m^2) (10,000 radians^2/second^2)
= 5,000 kg-m^2/s^2
Loss in Kinetic Energy:
The loss in kinetic energy is given by:
Loss in kinetic energy = K_initial_total - K_final
The loss in kinetic energy of the system can be calculated by considering the initial and final kinetic energy of the discs.
Initial Kinetic Energy:
The initial kinetic energy of the system is given by the sum of the kinetic energies of the individual discs. Since the discs are identical, their masses and moments of inertia are the same.
The kinetic energy of a rotating object is given by the formula:
K_initial = (1/2) I_initial ω^2
where K_initial is the initial kinetic energy, I_initial is the initial moment of inertia, and ω is the initial angular velocity.
Given that the moment of inertia of each disc is 1 kg-m^2 and the initial angular velocity is 100 radians/second, we can calculate the initial kinetic energy of each disc:
K_initial = (1/2) (1 kg-m^2) (100 radians/second)^2
= (1/2) (1 kg-m^2) (10,000 radians^2/second^2)
= 5,000 kg-m^2/s^2
Since there are two discs, the initial total kinetic energy of the system is:
K_initial_total = 2 × 5,000 kg-m^2/s^2
= 10,000 kg-m^2/s^2
Final Kinetic Energy:
When the second disc is gently placed on the first disc, the two discs start rotating together about the same axis. The final moment of inertia of the system can be obtained by considering the moment of inertia of each disc and the parallel axis theorem.
The parallel axis theorem states that the moment of inertia of an object about an axis parallel to and a distance 'd' away from the axis passing through its center is given by:
I_final = I_initial + md^2
where I_initial is the initial moment of inertia, m is the mass of the object, and d is the distance between the two axes.
Since the discs are identical and their centers coincide, the distance between the two axes is zero. Therefore, the final moment of inertia of the system remains the same as the initial moment of inertia:
I_final = I_initial
= 1 kg-m^2
The final angular velocity of the system can be calculated by applying the principle of conservation of angular momentum. Since there are no external torques acting on the system, the total angular momentum of the system remains constant.
Initial angular momentum = Final angular momentum
I_initial ω_initial = I_final ω_final
Substituting the values, we get:
(1 kg-m^2) (100 radians/second) = (1 kg-m^2) ω_final
ω_final = 100 radians/second
The final kinetic energy of the system can be calculated using the formula mentioned earlier:
K_final = (1/2) I_final ω_final^2
Substituting the values, we get:
K_final = (1/2) (1 kg-m^2) (100 radians/second)^2
= (1/2) (1 kg-m^2) (10,000 radians^2/second^2)
= 5,000 kg-m^2/s^2
Loss in Kinetic Energy:
The loss in kinetic energy is given by:
Loss in kinetic energy = K_initial_total - K_final

|
Explore Courses for JEE exam
|

|
Question Description
The moment of inertia of a uniform disc about an axis passing through its centre and perpendicular to its plane is 1kg - m2. It is rotating with an angular velocity 100 radians/second. Another identical disc is gently placed on it so that their centres coincide. Now these two discs together continue to rotate about the same axis. Then the loss in kinetic energy in kilo joules isa) 2.5 b) 3.0 c) 3.5 d) 4.0 Correct answer is option 'A'. Can you explain this answer? for JEE 2025 is part of JEE preparation. The Question and answers have been prepared according to the JEE exam syllabus. Information about The moment of inertia of a uniform disc about an axis passing through its centre and perpendicular to its plane is 1kg - m2. It is rotating with an angular velocity 100 radians/second. Another identical disc is gently placed on it so that their centres coincide. Now these two discs together continue to rotate about the same axis. Then the loss in kinetic energy in kilo joules isa) 2.5 b) 3.0 c) 3.5 d) 4.0 Correct answer is option 'A'. Can you explain this answer? covers all topics & solutions for JEE 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The moment of inertia of a uniform disc about an axis passing through its centre and perpendicular to its plane is 1kg - m2. It is rotating with an angular velocity 100 radians/second. Another identical disc is gently placed on it so that their centres coincide. Now these two discs together continue to rotate about the same axis. Then the loss in kinetic energy in kilo joules isa) 2.5 b) 3.0 c) 3.5 d) 4.0 Correct answer is option 'A'. Can you explain this answer?.
The moment of inertia of a uniform disc about an axis passing through its centre and perpendicular to its plane is 1kg - m2. It is rotating with an angular velocity 100 radians/second. Another identical disc is gently placed on it so that their centres coincide. Now these two discs together continue to rotate about the same axis. Then the loss in kinetic energy in kilo joules isa) 2.5 b) 3.0 c) 3.5 d) 4.0 Correct answer is option 'A'. Can you explain this answer? for JEE 2025 is part of JEE preparation. The Question and answers have been prepared according to the JEE exam syllabus. Information about The moment of inertia of a uniform disc about an axis passing through its centre and perpendicular to its plane is 1kg - m2. It is rotating with an angular velocity 100 radians/second. Another identical disc is gently placed on it so that their centres coincide. Now these two discs together continue to rotate about the same axis. Then the loss in kinetic energy in kilo joules isa) 2.5 b) 3.0 c) 3.5 d) 4.0 Correct answer is option 'A'. Can you explain this answer? covers all topics & solutions for JEE 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The moment of inertia of a uniform disc about an axis passing through its centre and perpendicular to its plane is 1kg - m2. It is rotating with an angular velocity 100 radians/second. Another identical disc is gently placed on it so that their centres coincide. Now these two discs together continue to rotate about the same axis. Then the loss in kinetic energy in kilo joules isa) 2.5 b) 3.0 c) 3.5 d) 4.0 Correct answer is option 'A'. Can you explain this answer?.
Solutions for The moment of inertia of a uniform disc about an axis passing through its centre and perpendicular to its plane is 1kg - m2. It is rotating with an angular velocity 100 radians/second. Another identical disc is gently placed on it so that their centres coincide. Now these two discs together continue to rotate about the same axis. Then the loss in kinetic energy in kilo joules isa) 2.5 b) 3.0 c) 3.5 d) 4.0 Correct answer is option 'A'. Can you explain this answer? in English & in Hindi are available as part of our courses for JEE.
Download more important topics, notes, lectures and mock test series for JEE Exam by signing up for free.
Here you can find the meaning of The moment of inertia of a uniform disc about an axis passing through its centre and perpendicular to its plane is 1kg - m2. It is rotating with an angular velocity 100 radians/second. Another identical disc is gently placed on it so that their centres coincide. Now these two discs together continue to rotate about the same axis. Then the loss in kinetic energy in kilo joules isa) 2.5 b) 3.0 c) 3.5 d) 4.0 Correct answer is option 'A'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
The moment of inertia of a uniform disc about an axis passing through its centre and perpendicular to its plane is 1kg - m2. It is rotating with an angular velocity 100 radians/second. Another identical disc is gently placed on it so that their centres coincide. Now these two discs together continue to rotate about the same axis. Then the loss in kinetic energy in kilo joules isa) 2.5 b) 3.0 c) 3.5 d) 4.0 Correct answer is option 'A'. Can you explain this answer?, a detailed solution for The moment of inertia of a uniform disc about an axis passing through its centre and perpendicular to its plane is 1kg - m2. It is rotating with an angular velocity 100 radians/second. Another identical disc is gently placed on it so that their centres coincide. Now these two discs together continue to rotate about the same axis. Then the loss in kinetic energy in kilo joules isa) 2.5 b) 3.0 c) 3.5 d) 4.0 Correct answer is option 'A'. Can you explain this answer? has been provided alongside types of The moment of inertia of a uniform disc about an axis passing through its centre and perpendicular to its plane is 1kg - m2. It is rotating with an angular velocity 100 radians/second. Another identical disc is gently placed on it so that their centres coincide. Now these two discs together continue to rotate about the same axis. Then the loss in kinetic energy in kilo joules isa) 2.5 b) 3.0 c) 3.5 d) 4.0 Correct answer is option 'A'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice The moment of inertia of a uniform disc about an axis passing through its centre and perpendicular to its plane is 1kg - m2. It is rotating with an angular velocity 100 radians/second. Another identical disc is gently placed on it so that their centres coincide. Now these two discs together continue to rotate about the same axis. Then the loss in kinetic energy in kilo joules isa) 2.5 b) 3.0 c) 3.5 d) 4.0 Correct answer is option 'A'. Can you explain this answer? tests, examples and also practice JEE tests.

|
Explore Courses for JEE exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















