Computer Science Engineering (CSE) Exam > Computer Science Engineering (CSE) Questions > Consider a simple graph with unit edge costs....
Start Learning for Free
Consider a simple graph with unit edge costs. Each node in the graph represents a router. Each node maintains a routing table indicating the next hop router to be used to relay a packet to its destination and the cost of the path to the destination through that router. Initially, the routing table is empty. The routing table is synchronously updated as follows. In each updation interval, three tasks are performed.
i. A node determines whether its neighbours in the graph are accessible. If so, it sets the tentative cost to each accessible neighbour as 1. Otherwise, the cost is set to ∞.
ii. From each accessible neighbour, it gets the costs to relay to other nodes via that neighbour (as the next hop).
iii. Each node updates its routing table based on the information received in the previous two steps by choosing the minimum cost.
i. A node determines whether its neighbours in the graph are accessible. If so, it sets the tentative cost to each accessible neighbour as 1. Otherwise, the cost is set to ∞.
ii. From each accessible neighbour, it gets the costs to relay to other nodes via that neighbour (as the next hop).
iii. Each node updates its routing table based on the information received in the previous two steps by choosing the minimum cost.
Continuing from the earlier problem, suppose at some time t, when the costs have stabilized, node A goes down. The cost from node F to node A at time (t + 100) is :
- a)> 100 but finite
- b)∞
- c)3
- d)> 3 and ≤ 100
Correct answer is option 'C'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
Consider a simple graph with unit edge costs. Each node in the graph r...
OPTION C
Here, we have to count average hops per message.
Steps -
1) Message goes up from sender to root
2) Message comes down from root to destination
Here, we have to count average hops per message.
Steps -
1) Message goes up from sender to root
2) Message comes down from root to destination
1) Average hops message goes to root - 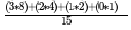
= 2.267
Here 3 * 8 represents 3 hops & 8 routers for Bottommost level & So on..
= 2.267
Here 3 * 8 represents 3 hops & 8 routers for Bottommost level & So on..
2) Similarly average hops when message comes down - 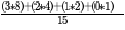
{Same as above}
So, Total Hops = 2 * 2.267 = 4.53 (Ans)
{Same as above}
So, Total Hops = 2 * 2.267 = 4.53 (Ans)

|
Explore Courses for Computer Science Engineering (CSE) exam
|

|
Similar Computer Science Engineering (CSE) Doubts
Consider a simple graph with unit edge costs. Each node in the graph represents a router. Each node maintains a routing table indicating the next hop router to be used to relay a packet to its destination and the cost of the path to the destination through that router. Initially, the routing table is empty. The routing table is synchronously updated as follows. In each updation interval, three tasks are performed.i. A node determines whether its neighbours in the graph are accessible. If so, it sets the tentative cost to each accessible neighbour as 1. Otherwise, the cost is set to ∞.ii. From each accessible neighbour, it gets the costs to relay to other nodes via that neighbour (as the next hop).iii. Each node updates its routing table based on the information received in the previous two steps by choosing the minimum cost.Continuing from the earlier problem, suppose at some time t, when the costs have stabilized, node A goes down. The cost from node F to node A at time (t + 100) is :a)> 100 but finiteb)∞c)3d)> 3 and≤ 100Correct answer is option 'C'. Can you explain this answer?
Question Description
Consider a simple graph with unit edge costs. Each node in the graph represents a router. Each node maintains a routing table indicating the next hop router to be used to relay a packet to its destination and the cost of the path to the destination through that router. Initially, the routing table is empty. The routing table is synchronously updated as follows. In each updation interval, three tasks are performed.i. A node determines whether its neighbours in the graph are accessible. If so, it sets the tentative cost to each accessible neighbour as 1. Otherwise, the cost is set to ∞.ii. From each accessible neighbour, it gets the costs to relay to other nodes via that neighbour (as the next hop).iii. Each node updates its routing table based on the information received in the previous two steps by choosing the minimum cost.Continuing from the earlier problem, suppose at some time t, when the costs have stabilized, node A goes down. The cost from node F to node A at time (t + 100) is :a)> 100 but finiteb)∞c)3d)> 3 and≤ 100Correct answer is option 'C'. Can you explain this answer? for Computer Science Engineering (CSE) 2024 is part of Computer Science Engineering (CSE) preparation. The Question and answers have been prepared according to the Computer Science Engineering (CSE) exam syllabus. Information about Consider a simple graph with unit edge costs. Each node in the graph represents a router. Each node maintains a routing table indicating the next hop router to be used to relay a packet to its destination and the cost of the path to the destination through that router. Initially, the routing table is empty. The routing table is synchronously updated as follows. In each updation interval, three tasks are performed.i. A node determines whether its neighbours in the graph are accessible. If so, it sets the tentative cost to each accessible neighbour as 1. Otherwise, the cost is set to ∞.ii. From each accessible neighbour, it gets the costs to relay to other nodes via that neighbour (as the next hop).iii. Each node updates its routing table based on the information received in the previous two steps by choosing the minimum cost.Continuing from the earlier problem, suppose at some time t, when the costs have stabilized, node A goes down. The cost from node F to node A at time (t + 100) is :a)> 100 but finiteb)∞c)3d)> 3 and≤ 100Correct answer is option 'C'. Can you explain this answer? covers all topics & solutions for Computer Science Engineering (CSE) 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Consider a simple graph with unit edge costs. Each node in the graph represents a router. Each node maintains a routing table indicating the next hop router to be used to relay a packet to its destination and the cost of the path to the destination through that router. Initially, the routing table is empty. The routing table is synchronously updated as follows. In each updation interval, three tasks are performed.i. A node determines whether its neighbours in the graph are accessible. If so, it sets the tentative cost to each accessible neighbour as 1. Otherwise, the cost is set to ∞.ii. From each accessible neighbour, it gets the costs to relay to other nodes via that neighbour (as the next hop).iii. Each node updates its routing table based on the information received in the previous two steps by choosing the minimum cost.Continuing from the earlier problem, suppose at some time t, when the costs have stabilized, node A goes down. The cost from node F to node A at time (t + 100) is :a)> 100 but finiteb)∞c)3d)> 3 and≤ 100Correct answer is option 'C'. Can you explain this answer?.
Consider a simple graph with unit edge costs. Each node in the graph represents a router. Each node maintains a routing table indicating the next hop router to be used to relay a packet to its destination and the cost of the path to the destination through that router. Initially, the routing table is empty. The routing table is synchronously updated as follows. In each updation interval, three tasks are performed.i. A node determines whether its neighbours in the graph are accessible. If so, it sets the tentative cost to each accessible neighbour as 1. Otherwise, the cost is set to ∞.ii. From each accessible neighbour, it gets the costs to relay to other nodes via that neighbour (as the next hop).iii. Each node updates its routing table based on the information received in the previous two steps by choosing the minimum cost.Continuing from the earlier problem, suppose at some time t, when the costs have stabilized, node A goes down. The cost from node F to node A at time (t + 100) is :a)> 100 but finiteb)∞c)3d)> 3 and≤ 100Correct answer is option 'C'. Can you explain this answer? for Computer Science Engineering (CSE) 2024 is part of Computer Science Engineering (CSE) preparation. The Question and answers have been prepared according to the Computer Science Engineering (CSE) exam syllabus. Information about Consider a simple graph with unit edge costs. Each node in the graph represents a router. Each node maintains a routing table indicating the next hop router to be used to relay a packet to its destination and the cost of the path to the destination through that router. Initially, the routing table is empty. The routing table is synchronously updated as follows. In each updation interval, three tasks are performed.i. A node determines whether its neighbours in the graph are accessible. If so, it sets the tentative cost to each accessible neighbour as 1. Otherwise, the cost is set to ∞.ii. From each accessible neighbour, it gets the costs to relay to other nodes via that neighbour (as the next hop).iii. Each node updates its routing table based on the information received in the previous two steps by choosing the minimum cost.Continuing from the earlier problem, suppose at some time t, when the costs have stabilized, node A goes down. The cost from node F to node A at time (t + 100) is :a)> 100 but finiteb)∞c)3d)> 3 and≤ 100Correct answer is option 'C'. Can you explain this answer? covers all topics & solutions for Computer Science Engineering (CSE) 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Consider a simple graph with unit edge costs. Each node in the graph represents a router. Each node maintains a routing table indicating the next hop router to be used to relay a packet to its destination and the cost of the path to the destination through that router. Initially, the routing table is empty. The routing table is synchronously updated as follows. In each updation interval, three tasks are performed.i. A node determines whether its neighbours in the graph are accessible. If so, it sets the tentative cost to each accessible neighbour as 1. Otherwise, the cost is set to ∞.ii. From each accessible neighbour, it gets the costs to relay to other nodes via that neighbour (as the next hop).iii. Each node updates its routing table based on the information received in the previous two steps by choosing the minimum cost.Continuing from the earlier problem, suppose at some time t, when the costs have stabilized, node A goes down. The cost from node F to node A at time (t + 100) is :a)> 100 but finiteb)∞c)3d)> 3 and≤ 100Correct answer is option 'C'. Can you explain this answer?.
Solutions for Consider a simple graph with unit edge costs. Each node in the graph represents a router. Each node maintains a routing table indicating the next hop router to be used to relay a packet to its destination and the cost of the path to the destination through that router. Initially, the routing table is empty. The routing table is synchronously updated as follows. In each updation interval, three tasks are performed.i. A node determines whether its neighbours in the graph are accessible. If so, it sets the tentative cost to each accessible neighbour as 1. Otherwise, the cost is set to ∞.ii. From each accessible neighbour, it gets the costs to relay to other nodes via that neighbour (as the next hop).iii. Each node updates its routing table based on the information received in the previous two steps by choosing the minimum cost.Continuing from the earlier problem, suppose at some time t, when the costs have stabilized, node A goes down. The cost from node F to node A at time (t + 100) is :a)> 100 but finiteb)∞c)3d)> 3 and≤ 100Correct answer is option 'C'. Can you explain this answer? in English & in Hindi are available as part of our courses for Computer Science Engineering (CSE).
Download more important topics, notes, lectures and mock test series for Computer Science Engineering (CSE) Exam by signing up for free.
Here you can find the meaning of Consider a simple graph with unit edge costs. Each node in the graph represents a router. Each node maintains a routing table indicating the next hop router to be used to relay a packet to its destination and the cost of the path to the destination through that router. Initially, the routing table is empty. The routing table is synchronously updated as follows. In each updation interval, three tasks are performed.i. A node determines whether its neighbours in the graph are accessible. If so, it sets the tentative cost to each accessible neighbour as 1. Otherwise, the cost is set to ∞.ii. From each accessible neighbour, it gets the costs to relay to other nodes via that neighbour (as the next hop).iii. Each node updates its routing table based on the information received in the previous two steps by choosing the minimum cost.Continuing from the earlier problem, suppose at some time t, when the costs have stabilized, node A goes down. The cost from node F to node A at time (t + 100) is :a)> 100 but finiteb)∞c)3d)> 3 and≤ 100Correct answer is option 'C'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Consider a simple graph with unit edge costs. Each node in the graph represents a router. Each node maintains a routing table indicating the next hop router to be used to relay a packet to its destination and the cost of the path to the destination through that router. Initially, the routing table is empty. The routing table is synchronously updated as follows. In each updation interval, three tasks are performed.i. A node determines whether its neighbours in the graph are accessible. If so, it sets the tentative cost to each accessible neighbour as 1. Otherwise, the cost is set to ∞.ii. From each accessible neighbour, it gets the costs to relay to other nodes via that neighbour (as the next hop).iii. Each node updates its routing table based on the information received in the previous two steps by choosing the minimum cost.Continuing from the earlier problem, suppose at some time t, when the costs have stabilized, node A goes down. The cost from node F to node A at time (t + 100) is :a)> 100 but finiteb)∞c)3d)> 3 and≤ 100Correct answer is option 'C'. Can you explain this answer?, a detailed solution for Consider a simple graph with unit edge costs. Each node in the graph represents a router. Each node maintains a routing table indicating the next hop router to be used to relay a packet to its destination and the cost of the path to the destination through that router. Initially, the routing table is empty. The routing table is synchronously updated as follows. In each updation interval, three tasks are performed.i. A node determines whether its neighbours in the graph are accessible. If so, it sets the tentative cost to each accessible neighbour as 1. Otherwise, the cost is set to ∞.ii. From each accessible neighbour, it gets the costs to relay to other nodes via that neighbour (as the next hop).iii. Each node updates its routing table based on the information received in the previous two steps by choosing the minimum cost.Continuing from the earlier problem, suppose at some time t, when the costs have stabilized, node A goes down. The cost from node F to node A at time (t + 100) is :a)> 100 but finiteb)∞c)3d)> 3 and≤ 100Correct answer is option 'C'. Can you explain this answer? has been provided alongside types of Consider a simple graph with unit edge costs. Each node in the graph represents a router. Each node maintains a routing table indicating the next hop router to be used to relay a packet to its destination and the cost of the path to the destination through that router. Initially, the routing table is empty. The routing table is synchronously updated as follows. In each updation interval, three tasks are performed.i. A node determines whether its neighbours in the graph are accessible. If so, it sets the tentative cost to each accessible neighbour as 1. Otherwise, the cost is set to ∞.ii. From each accessible neighbour, it gets the costs to relay to other nodes via that neighbour (as the next hop).iii. Each node updates its routing table based on the information received in the previous two steps by choosing the minimum cost.Continuing from the earlier problem, suppose at some time t, when the costs have stabilized, node A goes down. The cost from node F to node A at time (t + 100) is :a)> 100 but finiteb)∞c)3d)> 3 and≤ 100Correct answer is option 'C'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Consider a simple graph with unit edge costs. Each node in the graph represents a router. Each node maintains a routing table indicating the next hop router to be used to relay a packet to its destination and the cost of the path to the destination through that router. Initially, the routing table is empty. The routing table is synchronously updated as follows. In each updation interval, three tasks are performed.i. A node determines whether its neighbours in the graph are accessible. If so, it sets the tentative cost to each accessible neighbour as 1. Otherwise, the cost is set to ∞.ii. From each accessible neighbour, it gets the costs to relay to other nodes via that neighbour (as the next hop).iii. Each node updates its routing table based on the information received in the previous two steps by choosing the minimum cost.Continuing from the earlier problem, suppose at some time t, when the costs have stabilized, node A goes down. The cost from node F to node A at time (t + 100) is :a)> 100 but finiteb)∞c)3d)> 3 and≤ 100Correct answer is option 'C'. Can you explain this answer? tests, examples and also practice Computer Science Engineering (CSE) tests.

|
Explore Courses for Computer Science Engineering (CSE) exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.























