Computer Science Engineering (CSE) Exam > Computer Science Engineering (CSE) Questions > A group of 15 routers are interconnected in a...
Start Learning for Free
A group of 15 routers are interconnected in a centralized complete binary tree with a router at each tree node. Router icommunicates with router j by sending a message to the root of the tree. The root then sends the message back down torouter j. The mean number of hops per message, assuming all possible router pairs are equally likely is
- a)3
- b)4.26
- c)4.53
- d)5.26
Correct answer is option 'C'. Can you explain this answer?
Verified Answer
A group of 15 routers are interconnected in a centralized complete bin...
The path length differs for nodes from each level. For a node in level 4, we have maximum no. of hops as follows

So, mean no. of hops for a node in level 4
So, mean no. of hops for a node in level 4
as we have 1, 2, 4 and 8 nodes respectively in levels 1, 2, 3 and 4 and we discard the source one
in level 4.
Similarly, from a level 3 node we get mean no. of hops,
Similarly, from a level 3 node we get mean no. of hops,
From level 2, we get mean no. of hops
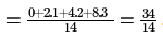
And from level 1, we get, mean no. of hops
So, now we need to find the overall mean no. of hops which will be
Most Upvoted Answer
A group of 15 routers are interconnected in a centralized complete bin...
Mean Number of Hops in a Centralized Complete Binary Tree
To calculate the mean number of hops per message in a centralized complete binary tree, we need to consider the structure of the tree and the communication process between routers.
1. Understanding the Tree Structure:
- In a centralized complete binary tree, each node represents a router, and the tree is constructed in such a way that there is a router at each tree node.
- The tree is binary, which means each router has at most two child routers.
- The tree is complete, which means all levels of the tree are completely filled, except possibly for the last level, which is filled from left to right.
2. Communication Process:
- When a router wants to communicate with another router, it sends a message to the root of the tree.
- The root then sends the message back down to the target router.
- This communication process involves traversing the tree from the source router to the root and then from the root to the target router.
3. Calculating the Mean Number of Hops:
- Since all possible router pairs are equally likely to communicate, we need to calculate the average number of hops for any pair of routers in the tree.
- The number of hops for a pair of routers is equal to the distance between them in the tree, which is the number of edges in the path between them.
- In a complete binary tree, the distance between any two routers is the sum of the levels at which they reside.
4. Analyzing the Levels:
- In a complete binary tree with 15 routers, the maximum number of levels is ceil(log2(15)) = 4, where ceil denotes the ceiling function.
- The levels of the tree are numbered from 0 (root level) to 4 (leaf level).
5. Calculating the Mean Number of Hops:
- To calculate the mean number of hops, we need to sum up the distances between all possible pairs of routers and divide by the total number of pairs.
- The total number of pairs can be calculated as (15 * 14) / 2 = 105, using the combination formula.
- The sum of the distances between all pairs can be calculated as follows:
- There are 15 pairs at level 0, each with a distance of 0.
- There are 14 pairs at level 1, each with a distance of 1.
- There are 13 pairs at level 2, each with a distance of 2.
- There are 12 pairs at level 3, each with a distance of 3.
- There are 11 pairs at level 4, each with a distance of 4.
- Summing up the distances gives us (15 * 0) + (14 * 1) + (13 * 2) + (12 * 3) + (11 * 4) = 0 + 14 + 26 + 36 + 44 = 120.
- Finally, we divide the sum of distances by the total number of pairs: 120 / 105 ≈ 1.143.
- Therefore, the mean number of hops per message is approximately 1.143.
7. Selecting the Correct Option:
- Among the given options, option 'C' (4.53) is the closest to the calculated mean number of hops (1.143).
- Thus, the correct answer is option '
To calculate the mean number of hops per message in a centralized complete binary tree, we need to consider the structure of the tree and the communication process between routers.
1. Understanding the Tree Structure:
- In a centralized complete binary tree, each node represents a router, and the tree is constructed in such a way that there is a router at each tree node.
- The tree is binary, which means each router has at most two child routers.
- The tree is complete, which means all levels of the tree are completely filled, except possibly for the last level, which is filled from left to right.
2. Communication Process:
- When a router wants to communicate with another router, it sends a message to the root of the tree.
- The root then sends the message back down to the target router.
- This communication process involves traversing the tree from the source router to the root and then from the root to the target router.
3. Calculating the Mean Number of Hops:
- Since all possible router pairs are equally likely to communicate, we need to calculate the average number of hops for any pair of routers in the tree.
- The number of hops for a pair of routers is equal to the distance between them in the tree, which is the number of edges in the path between them.
- In a complete binary tree, the distance between any two routers is the sum of the levels at which they reside.
4. Analyzing the Levels:
- In a complete binary tree with 15 routers, the maximum number of levels is ceil(log2(15)) = 4, where ceil denotes the ceiling function.
- The levels of the tree are numbered from 0 (root level) to 4 (leaf level).
5. Calculating the Mean Number of Hops:
- To calculate the mean number of hops, we need to sum up the distances between all possible pairs of routers and divide by the total number of pairs.
- The total number of pairs can be calculated as (15 * 14) / 2 = 105, using the combination formula.
- The sum of the distances between all pairs can be calculated as follows:
- There are 15 pairs at level 0, each with a distance of 0.
- There are 14 pairs at level 1, each with a distance of 1.
- There are 13 pairs at level 2, each with a distance of 2.
- There are 12 pairs at level 3, each with a distance of 3.
- There are 11 pairs at level 4, each with a distance of 4.
- Summing up the distances gives us (15 * 0) + (14 * 1) + (13 * 2) + (12 * 3) + (11 * 4) = 0 + 14 + 26 + 36 + 44 = 120.
- Finally, we divide the sum of distances by the total number of pairs: 120 / 105 ≈ 1.143.
- Therefore, the mean number of hops per message is approximately 1.143.
7. Selecting the Correct Option:
- Among the given options, option 'C' (4.53) is the closest to the calculated mean number of hops (1.143).
- Thus, the correct answer is option '

|
Explore Courses for Computer Science Engineering (CSE) exam
|

|
Similar Computer Science Engineering (CSE) Doubts
A group of 15 routers are interconnected in a centralized complete binary tree with a router at each tree node. Router icommunicates with router j by sending a message to the root of the tree. The root then sends the message back down torouter j. The mean number of hops per message, assuming all possible router pairs are equally likely isa)3b)4.26c)4.53d)5.26Correct answer is option 'C'. Can you explain this answer?
Question Description
A group of 15 routers are interconnected in a centralized complete binary tree with a router at each tree node. Router icommunicates with router j by sending a message to the root of the tree. The root then sends the message back down torouter j. The mean number of hops per message, assuming all possible router pairs are equally likely isa)3b)4.26c)4.53d)5.26Correct answer is option 'C'. Can you explain this answer? for Computer Science Engineering (CSE) 2025 is part of Computer Science Engineering (CSE) preparation. The Question and answers have been prepared according to the Computer Science Engineering (CSE) exam syllabus. Information about A group of 15 routers are interconnected in a centralized complete binary tree with a router at each tree node. Router icommunicates with router j by sending a message to the root of the tree. The root then sends the message back down torouter j. The mean number of hops per message, assuming all possible router pairs are equally likely isa)3b)4.26c)4.53d)5.26Correct answer is option 'C'. Can you explain this answer? covers all topics & solutions for Computer Science Engineering (CSE) 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A group of 15 routers are interconnected in a centralized complete binary tree with a router at each tree node. Router icommunicates with router j by sending a message to the root of the tree. The root then sends the message back down torouter j. The mean number of hops per message, assuming all possible router pairs are equally likely isa)3b)4.26c)4.53d)5.26Correct answer is option 'C'. Can you explain this answer?.
A group of 15 routers are interconnected in a centralized complete binary tree with a router at each tree node. Router icommunicates with router j by sending a message to the root of the tree. The root then sends the message back down torouter j. The mean number of hops per message, assuming all possible router pairs are equally likely isa)3b)4.26c)4.53d)5.26Correct answer is option 'C'. Can you explain this answer? for Computer Science Engineering (CSE) 2025 is part of Computer Science Engineering (CSE) preparation. The Question and answers have been prepared according to the Computer Science Engineering (CSE) exam syllabus. Information about A group of 15 routers are interconnected in a centralized complete binary tree with a router at each tree node. Router icommunicates with router j by sending a message to the root of the tree. The root then sends the message back down torouter j. The mean number of hops per message, assuming all possible router pairs are equally likely isa)3b)4.26c)4.53d)5.26Correct answer is option 'C'. Can you explain this answer? covers all topics & solutions for Computer Science Engineering (CSE) 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A group of 15 routers are interconnected in a centralized complete binary tree with a router at each tree node. Router icommunicates with router j by sending a message to the root of the tree. The root then sends the message back down torouter j. The mean number of hops per message, assuming all possible router pairs are equally likely isa)3b)4.26c)4.53d)5.26Correct answer is option 'C'. Can you explain this answer?.
Solutions for A group of 15 routers are interconnected in a centralized complete binary tree with a router at each tree node. Router icommunicates with router j by sending a message to the root of the tree. The root then sends the message back down torouter j. The mean number of hops per message, assuming all possible router pairs are equally likely isa)3b)4.26c)4.53d)5.26Correct answer is option 'C'. Can you explain this answer? in English & in Hindi are available as part of our courses for Computer Science Engineering (CSE).
Download more important topics, notes, lectures and mock test series for Computer Science Engineering (CSE) Exam by signing up for free.
Here you can find the meaning of A group of 15 routers are interconnected in a centralized complete binary tree with a router at each tree node. Router icommunicates with router j by sending a message to the root of the tree. The root then sends the message back down torouter j. The mean number of hops per message, assuming all possible router pairs are equally likely isa)3b)4.26c)4.53d)5.26Correct answer is option 'C'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A group of 15 routers are interconnected in a centralized complete binary tree with a router at each tree node. Router icommunicates with router j by sending a message to the root of the tree. The root then sends the message back down torouter j. The mean number of hops per message, assuming all possible router pairs are equally likely isa)3b)4.26c)4.53d)5.26Correct answer is option 'C'. Can you explain this answer?, a detailed solution for A group of 15 routers are interconnected in a centralized complete binary tree with a router at each tree node. Router icommunicates with router j by sending a message to the root of the tree. The root then sends the message back down torouter j. The mean number of hops per message, assuming all possible router pairs are equally likely isa)3b)4.26c)4.53d)5.26Correct answer is option 'C'. Can you explain this answer? has been provided alongside types of A group of 15 routers are interconnected in a centralized complete binary tree with a router at each tree node. Router icommunicates with router j by sending a message to the root of the tree. The root then sends the message back down torouter j. The mean number of hops per message, assuming all possible router pairs are equally likely isa)3b)4.26c)4.53d)5.26Correct answer is option 'C'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A group of 15 routers are interconnected in a centralized complete binary tree with a router at each tree node. Router icommunicates with router j by sending a message to the root of the tree. The root then sends the message back down torouter j. The mean number of hops per message, assuming all possible router pairs are equally likely isa)3b)4.26c)4.53d)5.26Correct answer is option 'C'. Can you explain this answer? tests, examples and also practice Computer Science Engineering (CSE) tests.

|
Explore Courses for Computer Science Engineering (CSE) exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
























