Class 11 Exam > Class 11 Questions > N identical cubes each of mass m and side l a...
Start Learning for Free
N identical cubes each of mass m and side l are on the horizontal surface. Then the minimum amount of work done to arrange them one on the other is?
Most Upvoted Answer
N identical cubes each of mass m and side l are on the horizontal surf...
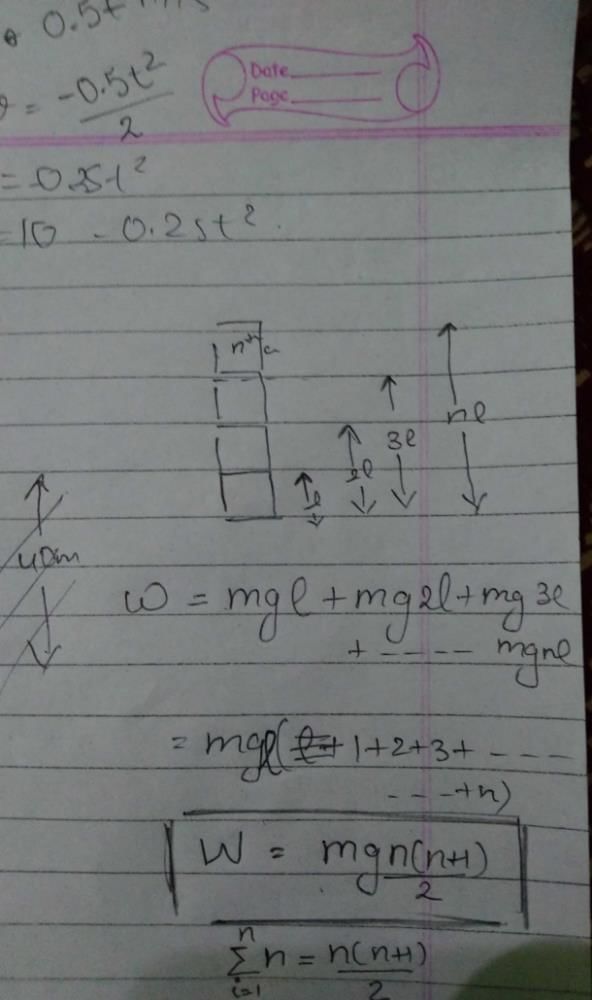
Community Answer
N identical cubes each of mass m and side l are on the horizontal surf...
Problem Statement:
N identical cubes, each of mass m and side length l, are placed on a horizontal surface. The task is to find the minimum amount of work required to arrange them one on top of the other.
Solution:
To solve this problem, we need to consider the forces acting on each cube and the work required to arrange them one on top of the other. Let's break down the solution into the following steps:
Step 1: Identifying the forces:
When a cube is placed on a horizontal surface, two forces act on it:
1. Weight (mg): This force acts vertically downwards due to the gravitational pull on the cube. The weight of each cube is given by the product of its mass (m) and the acceleration due to gravity (g).
2. Normal force (N): This force acts perpendicular to the surface and counterbalances the weight of the cube. It prevents the cube from sinking into the surface.
Step 2: Analyzing the work required:
To arrange the cubes one on top of the other, we need to lift each cube against the force of gravity. The work done in lifting a cube to a certain height is given by the product of the force applied and the distance moved.
The work done to lift the first cube (at the bottom) is zero since it is already on the surface. As we stack the cubes, the work required to lift each subsequent cube increases.
Step 3: Calculating the minimum work:
To minimize the work required, we need to arrange the cubes in such a way that the total distance traveled by each cube is minimized. This can be achieved by arranging the cubes in a pyramid-like structure.
Let's consider a stack of cubes as an example:
____
| |
|____|
| |
|____|
| |
|____|
In this arrangement, the distance traveled by each cube is equal to the height of the pyramid (h) multiplied by the number of cubes (N). Therefore, the total work required is given by:
Work = force × distance
= (mg) × (h × N)
Step 4: Simplifying the equation:
Since all the cubes are identical, the weight and mass of each cube are the same. Therefore, we can simplify the equation as:
Work = (m × g) × (h × N)
= (mgh) × N
Step 5: Final answer:
From the equation above, we can see that the minimum work required to arrange N identical cubes one on top of the other is given by:
Minimum Work = (mgh) × N
Thus, the minimum amount of work done to arrange N identical cubes one on top of the other is (mgh) × N, where m is the mass of each cube, g is the acceleration due to gravity, h is the height of the pyramid, and N is the total number of cubes.
N identical cubes, each of mass m and side length l, are placed on a horizontal surface. The task is to find the minimum amount of work required to arrange them one on top of the other.
Solution:
To solve this problem, we need to consider the forces acting on each cube and the work required to arrange them one on top of the other. Let's break down the solution into the following steps:
Step 1: Identifying the forces:
When a cube is placed on a horizontal surface, two forces act on it:
1. Weight (mg): This force acts vertically downwards due to the gravitational pull on the cube. The weight of each cube is given by the product of its mass (m) and the acceleration due to gravity (g).
2. Normal force (N): This force acts perpendicular to the surface and counterbalances the weight of the cube. It prevents the cube from sinking into the surface.
Step 2: Analyzing the work required:
To arrange the cubes one on top of the other, we need to lift each cube against the force of gravity. The work done in lifting a cube to a certain height is given by the product of the force applied and the distance moved.
The work done to lift the first cube (at the bottom) is zero since it is already on the surface. As we stack the cubes, the work required to lift each subsequent cube increases.
Step 3: Calculating the minimum work:
To minimize the work required, we need to arrange the cubes in such a way that the total distance traveled by each cube is minimized. This can be achieved by arranging the cubes in a pyramid-like structure.
Let's consider a stack of cubes as an example:
____
| |
|____|
| |
|____|
| |
|____|
In this arrangement, the distance traveled by each cube is equal to the height of the pyramid (h) multiplied by the number of cubes (N). Therefore, the total work required is given by:
Work = force × distance
= (mg) × (h × N)
Step 4: Simplifying the equation:
Since all the cubes are identical, the weight and mass of each cube are the same. Therefore, we can simplify the equation as:
Work = (m × g) × (h × N)
= (mgh) × N
Step 5: Final answer:
From the equation above, we can see that the minimum work required to arrange N identical cubes one on top of the other is given by:
Minimum Work = (mgh) × N
Thus, the minimum amount of work done to arrange N identical cubes one on top of the other is (mgh) × N, where m is the mass of each cube, g is the acceleration due to gravity, h is the height of the pyramid, and N is the total number of cubes.
Attention Class 11 Students!
To make sure you are not studying endlessly, EduRev has designed Class 11 study material, with Structured Courses, Videos, & Test Series. Plus get personalized analysis, doubt solving and improvement plans to achieve a great score in Class 11.

|
Explore Courses for Class 11 exam
|

|
Similar Class 11 Doubts
N identical cubes each of mass m and side l are on the horizontal surface. Then the minimum amount of work done to arrange them one on the other is?
Question Description
N identical cubes each of mass m and side l are on the horizontal surface. Then the minimum amount of work done to arrange them one on the other is? for Class 11 2024 is part of Class 11 preparation. The Question and answers have been prepared according to the Class 11 exam syllabus. Information about N identical cubes each of mass m and side l are on the horizontal surface. Then the minimum amount of work done to arrange them one on the other is? covers all topics & solutions for Class 11 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for N identical cubes each of mass m and side l are on the horizontal surface. Then the minimum amount of work done to arrange them one on the other is?.
N identical cubes each of mass m and side l are on the horizontal surface. Then the minimum amount of work done to arrange them one on the other is? for Class 11 2024 is part of Class 11 preparation. The Question and answers have been prepared according to the Class 11 exam syllabus. Information about N identical cubes each of mass m and side l are on the horizontal surface. Then the minimum amount of work done to arrange them one on the other is? covers all topics & solutions for Class 11 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for N identical cubes each of mass m and side l are on the horizontal surface. Then the minimum amount of work done to arrange them one on the other is?.
Solutions for N identical cubes each of mass m and side l are on the horizontal surface. Then the minimum amount of work done to arrange them one on the other is? in English & in Hindi are available as part of our courses for Class 11.
Download more important topics, notes, lectures and mock test series for Class 11 Exam by signing up for free.
Here you can find the meaning of N identical cubes each of mass m and side l are on the horizontal surface. Then the minimum amount of work done to arrange them one on the other is? defined & explained in the simplest way possible. Besides giving the explanation of
N identical cubes each of mass m and side l are on the horizontal surface. Then the minimum amount of work done to arrange them one on the other is?, a detailed solution for N identical cubes each of mass m and side l are on the horizontal surface. Then the minimum amount of work done to arrange them one on the other is? has been provided alongside types of N identical cubes each of mass m and side l are on the horizontal surface. Then the minimum amount of work done to arrange them one on the other is? theory, EduRev gives you an
ample number of questions to practice N identical cubes each of mass m and side l are on the horizontal surface. Then the minimum amount of work done to arrange them one on the other is? tests, examples and also practice Class 11 tests.

|
Explore Courses for Class 11 exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.

























