Class 12 Exam > Class 12 Questions > A square shaped coil of side 20cm is rotating...
Start Learning for Free
A square shaped coil of side 20cm is rotating at 60 revolution per minute in a magnetic field of 100 revolution of 100T no. Of turns thousands ,find maximum emf developed across the coil.?
Verified Answer
A square shaped coil of side 20cm is rotating at 60 revolution per min...
When a coil is turned in constant magnetic field then maximum induced EMF is given by formula
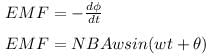
now from above equation the maximum value is defined as
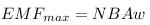
N = number of turns = 1
w = angular speed
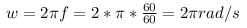
A = area = 0.2* 0.2 = 0.04 m^2
B = magnetic field = 100 T
Now by above formula
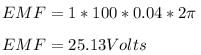
So maximum value of induced EMF will be 25.13 Volts
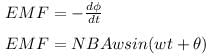
now from above equation the maximum value is defined as
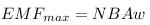
N = number of turns = 1
w = angular speed
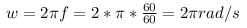
A = area = 0.2* 0.2 = 0.04 m^2
B = magnetic field = 100 T
Now by above formula
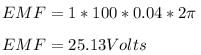
So maximum value of induced EMF will be 25.13 Volts
 This question is part of UPSC exam. View all Class 12 courses
This question is part of UPSC exam. View all Class 12 courses
Most Upvoted Answer
A square shaped coil of side 20cm is rotating at 60 revolution per min...
Given:
- Side of the square coil (l) = 20 cm = 0.2 m
- Number of turns in thousands (N) = 1000
- Rotational speed (n) = 60 revolutions per minute
- Magnetic field strength (B) = 100 T
To find:
The maximum emf developed across the coil.
Solution:
Step 1: Calculate the angular velocity (ω)
The angular velocity is the rate at which the coil rotates in radians per second. It can be calculated using the formula:
ω = 2πn
Where,
n = rotational speed in revolutions per minute
Substituting the given value:
ω = 2π * 60 = 120π rad/s
Step 2: Calculate the magnetic flux (Φ)
The magnetic flux through the coil can be calculated using the formula:
Φ = B * A
Where,
B = magnetic field strength
A = area of the coil
Since the coil is square-shaped, the area can be calculated as:
A = l^2
Substituting the given value:
A = (0.2)^2 = 0.04 m^2
Φ = 100 * 0.04 = 4 Tm^2
Step 3: Calculate the maximum emf (ε)
The maximum emf developed across the coil can be calculated using Faraday's law of electromagnetic induction:
ε = -N * dΦ/dt
Where,
N = number of turns
dΦ/dt = rate of change of magnetic flux
Since the coil is rotating, the rate of change of magnetic flux can be calculated as:
dΦ/dt = d(Φ*cos(ωt))/dt
Taking the derivative:
dΦ/dt = -ωΦ*sin(ωt)
Substituting the given values:
dΦ/dt = -120π * 4 * sin(ωt)
Since we are interested in the maximum emf, we can substitute the maximum value of sin(ωt), which is 1:
dΦ/dt = -120π * 4 * 1 = -480π
Now, substituting the values in the formula for ε:
ε = -N * dΦ/dt
= -1000 * (-480π)
= 480,000π T/s
Step 4: Convert the emf to volts
To convert the emf from teslas per second to volts, we use the conversion factor:
1 T/s = 1 V
Therefore, the maximum emf developed across the coil is:
ε = 480,000π V/s
Hence, the maximum emf developed across the coil is 480,000π V/s.
- Side of the square coil (l) = 20 cm = 0.2 m
- Number of turns in thousands (N) = 1000
- Rotational speed (n) = 60 revolutions per minute
- Magnetic field strength (B) = 100 T
To find:
The maximum emf developed across the coil.
Solution:
Step 1: Calculate the angular velocity (ω)
The angular velocity is the rate at which the coil rotates in radians per second. It can be calculated using the formula:
ω = 2πn
Where,
n = rotational speed in revolutions per minute
Substituting the given value:
ω = 2π * 60 = 120π rad/s
Step 2: Calculate the magnetic flux (Φ)
The magnetic flux through the coil can be calculated using the formula:
Φ = B * A
Where,
B = magnetic field strength
A = area of the coil
Since the coil is square-shaped, the area can be calculated as:
A = l^2
Substituting the given value:
A = (0.2)^2 = 0.04 m^2
Φ = 100 * 0.04 = 4 Tm^2
Step 3: Calculate the maximum emf (ε)
The maximum emf developed across the coil can be calculated using Faraday's law of electromagnetic induction:
ε = -N * dΦ/dt
Where,
N = number of turns
dΦ/dt = rate of change of magnetic flux
Since the coil is rotating, the rate of change of magnetic flux can be calculated as:
dΦ/dt = d(Φ*cos(ωt))/dt
Taking the derivative:
dΦ/dt = -ωΦ*sin(ωt)
Substituting the given values:
dΦ/dt = -120π * 4 * sin(ωt)
Since we are interested in the maximum emf, we can substitute the maximum value of sin(ωt), which is 1:
dΦ/dt = -120π * 4 * 1 = -480π
Now, substituting the values in the formula for ε:
ε = -N * dΦ/dt
= -1000 * (-480π)
= 480,000π T/s
Step 4: Convert the emf to volts
To convert the emf from teslas per second to volts, we use the conversion factor:
1 T/s = 1 V
Therefore, the maximum emf developed across the coil is:
ε = 480,000π V/s
Hence, the maximum emf developed across the coil is 480,000π V/s.

|
Explore Courses for Class 12 exam
|

|
Similar Class 12 Doubts
A square shaped coil of side 20cm is rotating at 60 revolution per minute in a magnetic field of 100 revolution of 100T no. Of turns thousands ,find maximum emf developed across the coil.?
Question Description
A square shaped coil of side 20cm is rotating at 60 revolution per minute in a magnetic field of 100 revolution of 100T no. Of turns thousands ,find maximum emf developed across the coil.? for Class 12 2024 is part of Class 12 preparation. The Question and answers have been prepared according to the Class 12 exam syllabus. Information about A square shaped coil of side 20cm is rotating at 60 revolution per minute in a magnetic field of 100 revolution of 100T no. Of turns thousands ,find maximum emf developed across the coil.? covers all topics & solutions for Class 12 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A square shaped coil of side 20cm is rotating at 60 revolution per minute in a magnetic field of 100 revolution of 100T no. Of turns thousands ,find maximum emf developed across the coil.?.
A square shaped coil of side 20cm is rotating at 60 revolution per minute in a magnetic field of 100 revolution of 100T no. Of turns thousands ,find maximum emf developed across the coil.? for Class 12 2024 is part of Class 12 preparation. The Question and answers have been prepared according to the Class 12 exam syllabus. Information about A square shaped coil of side 20cm is rotating at 60 revolution per minute in a magnetic field of 100 revolution of 100T no. Of turns thousands ,find maximum emf developed across the coil.? covers all topics & solutions for Class 12 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A square shaped coil of side 20cm is rotating at 60 revolution per minute in a magnetic field of 100 revolution of 100T no. Of turns thousands ,find maximum emf developed across the coil.?.
Solutions for A square shaped coil of side 20cm is rotating at 60 revolution per minute in a magnetic field of 100 revolution of 100T no. Of turns thousands ,find maximum emf developed across the coil.? in English & in Hindi are available as part of our courses for Class 12.
Download more important topics, notes, lectures and mock test series for Class 12 Exam by signing up for free.
Here you can find the meaning of A square shaped coil of side 20cm is rotating at 60 revolution per minute in a magnetic field of 100 revolution of 100T no. Of turns thousands ,find maximum emf developed across the coil.? defined & explained in the simplest way possible. Besides giving the explanation of
A square shaped coil of side 20cm is rotating at 60 revolution per minute in a magnetic field of 100 revolution of 100T no. Of turns thousands ,find maximum emf developed across the coil.?, a detailed solution for A square shaped coil of side 20cm is rotating at 60 revolution per minute in a magnetic field of 100 revolution of 100T no. Of turns thousands ,find maximum emf developed across the coil.? has been provided alongside types of A square shaped coil of side 20cm is rotating at 60 revolution per minute in a magnetic field of 100 revolution of 100T no. Of turns thousands ,find maximum emf developed across the coil.? theory, EduRev gives you an
ample number of questions to practice A square shaped coil of side 20cm is rotating at 60 revolution per minute in a magnetic field of 100 revolution of 100T no. Of turns thousands ,find maximum emf developed across the coil.? tests, examples and also practice Class 12 tests.

|
Explore Courses for Class 12 exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.



















