JEE Exam > JEE Questions > A rectangle ABCD of dimensions r and 2r is fo...
Start Learning for Free
A rectangle ABCD of dimensions r and 2r is folded along diagonal BD such that planes ABD and CBD are perpendicular to each other. Let the position of the vertex A remains unchanged and C1 is the new position of C.
If ∠∠ABC1 = θ, then cos θ is equal to
If ∠∠ABC1 = θ, then cos θ is equal to
- a)1/5
- b)2/5
- c)2/√5
- d)4/5
Correct answer is option 'B'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
A rectangle ABCD of dimensions r and 2r is folded along diagonal BD su...
Let the rectangle ABCD initially lies in xy plane with B King at origin BC' along x - axis and BA
Along y-axis.
Equation of BD in xy-plane is y = 2x
So. the coordinates of foot N of C on BD are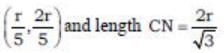
Clearly. CN = C1N
Hence, the coordinates of various points in 3-D are
A(0, r, 0), C(r, 0 , 0) , D (r, 2r, 0),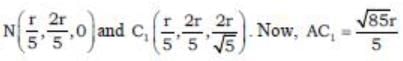
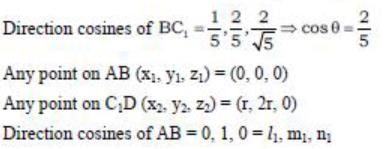
Along y-axis.
Equation of BD in xy-plane is y = 2x
So. the coordinates of foot N of C on BD are
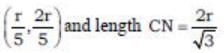
Clearly. CN = C1N
Hence, the coordinates of various points in 3-D are
A(0, r, 0), C(r, 0 , 0) , D (r, 2r, 0),
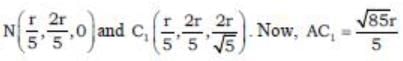
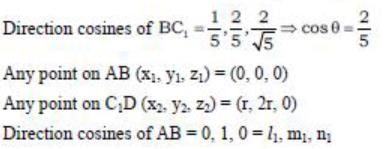
Most Upvoted Answer
A rectangle ABCD of dimensions r and 2r is folded along diagonal BD su...
To solve the problem, we need to analyze the geometric situation after the rectangle ABCD is folded along diagonal BD.
Initial Rectangle Setup
- Let the rectangle ABCD have vertices:
A(0, 0), B(r, 0), C(r, 2r), D(0, 2r)
- The diagonal BD connects points B and D.
Folding Mechanism
- When folded along BD, planes ABD and CBD become perpendicular.
- The point A remains fixed at (0, 0), while point C moves to a new position C1.
Determining New Position of C1
- The diagonal BD can be represented by the line equation:
y = -2x + 2r
- When C is folded, it reflects over line BD, resulting in coordinates for C1.
Angle Calculation
- To find cos(θ), we need to calculate the angle ABC1.
- The vectors involved are:
- AB = (r, 0)
- BC1 = (C1_x - r, C1_y)
- By using the dot product, we can express cos(θ) as follows:
cos(θ) = (AB · BC1) / (|AB| |BC1|)
Length and Dot Product
- The length |AB| = r.
- The calculation for |BC1| involves the coordinates of C1 after the fold.
- After computing the necessary values through the folding geometry, we find:
cos(θ) = 2/5.
Conclusion
Thus, the correct answer is option 'B', where cos(θ) = 2/5. This result arises from the geometric properties of reflection and the Pythagorean theorem applied to the new triangle formed by points A, B, and C1.
Initial Rectangle Setup
- Let the rectangle ABCD have vertices:
A(0, 0), B(r, 0), C(r, 2r), D(0, 2r)
- The diagonal BD connects points B and D.
Folding Mechanism
- When folded along BD, planes ABD and CBD become perpendicular.
- The point A remains fixed at (0, 0), while point C moves to a new position C1.
Determining New Position of C1
- The diagonal BD can be represented by the line equation:
y = -2x + 2r
- When C is folded, it reflects over line BD, resulting in coordinates for C1.
Angle Calculation
- To find cos(θ), we need to calculate the angle ABC1.
- The vectors involved are:
- AB = (r, 0)
- BC1 = (C1_x - r, C1_y)
- By using the dot product, we can express cos(θ) as follows:
cos(θ) = (AB · BC1) / (|AB| |BC1|)
Length and Dot Product
- The length |AB| = r.
- The calculation for |BC1| involves the coordinates of C1 after the fold.
- After computing the necessary values through the folding geometry, we find:
cos(θ) = 2/5.
Conclusion
Thus, the correct answer is option 'B', where cos(θ) = 2/5. This result arises from the geometric properties of reflection and the Pythagorean theorem applied to the new triangle formed by points A, B, and C1.
Attention JEE Students!
To make sure you are not studying endlessly, EduRev has designed JEE study material, with Structured Courses, Videos, & Test Series. Plus get personalized analysis, doubt solving and improvement plans to achieve a great score in JEE.

|
Explore Courses for JEE exam
|

|
Similar JEE Doubts
A rectangle ABCD of dimensions r and 2r is folded along diagonal BD such that planes ABD and CBD are perpendicular to each other. Let the position of the vertex A remains unchanged and C1is the new position of C.If∠∠ABC1= θ, then cos θ is equal toa)1/5b)2/5c)2/√5d)4/5Correct answer is option 'B'. Can you explain this answer?
Question Description
A rectangle ABCD of dimensions r and 2r is folded along diagonal BD such that planes ABD and CBD are perpendicular to each other. Let the position of the vertex A remains unchanged and C1is the new position of C.If∠∠ABC1= θ, then cos θ is equal toa)1/5b)2/5c)2/√5d)4/5Correct answer is option 'B'. Can you explain this answer? for JEE 2024 is part of JEE preparation. The Question and answers have been prepared according to the JEE exam syllabus. Information about A rectangle ABCD of dimensions r and 2r is folded along diagonal BD such that planes ABD and CBD are perpendicular to each other. Let the position of the vertex A remains unchanged and C1is the new position of C.If∠∠ABC1= θ, then cos θ is equal toa)1/5b)2/5c)2/√5d)4/5Correct answer is option 'B'. Can you explain this answer? covers all topics & solutions for JEE 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A rectangle ABCD of dimensions r and 2r is folded along diagonal BD such that planes ABD and CBD are perpendicular to each other. Let the position of the vertex A remains unchanged and C1is the new position of C.If∠∠ABC1= θ, then cos θ is equal toa)1/5b)2/5c)2/√5d)4/5Correct answer is option 'B'. Can you explain this answer?.
A rectangle ABCD of dimensions r and 2r is folded along diagonal BD such that planes ABD and CBD are perpendicular to each other. Let the position of the vertex A remains unchanged and C1is the new position of C.If∠∠ABC1= θ, then cos θ is equal toa)1/5b)2/5c)2/√5d)4/5Correct answer is option 'B'. Can you explain this answer? for JEE 2024 is part of JEE preparation. The Question and answers have been prepared according to the JEE exam syllabus. Information about A rectangle ABCD of dimensions r and 2r is folded along diagonal BD such that planes ABD and CBD are perpendicular to each other. Let the position of the vertex A remains unchanged and C1is the new position of C.If∠∠ABC1= θ, then cos θ is equal toa)1/5b)2/5c)2/√5d)4/5Correct answer is option 'B'. Can you explain this answer? covers all topics & solutions for JEE 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A rectangle ABCD of dimensions r and 2r is folded along diagonal BD such that planes ABD and CBD are perpendicular to each other. Let the position of the vertex A remains unchanged and C1is the new position of C.If∠∠ABC1= θ, then cos θ is equal toa)1/5b)2/5c)2/√5d)4/5Correct answer is option 'B'. Can you explain this answer?.
Solutions for A rectangle ABCD of dimensions r and 2r is folded along diagonal BD such that planes ABD and CBD are perpendicular to each other. Let the position of the vertex A remains unchanged and C1is the new position of C.If∠∠ABC1= θ, then cos θ is equal toa)1/5b)2/5c)2/√5d)4/5Correct answer is option 'B'. Can you explain this answer? in English & in Hindi are available as part of our courses for JEE.
Download more important topics, notes, lectures and mock test series for JEE Exam by signing up for free.
Here you can find the meaning of A rectangle ABCD of dimensions r and 2r is folded along diagonal BD such that planes ABD and CBD are perpendicular to each other. Let the position of the vertex A remains unchanged and C1is the new position of C.If∠∠ABC1= θ, then cos θ is equal toa)1/5b)2/5c)2/√5d)4/5Correct answer is option 'B'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A rectangle ABCD of dimensions r and 2r is folded along diagonal BD such that planes ABD and CBD are perpendicular to each other. Let the position of the vertex A remains unchanged and C1is the new position of C.If∠∠ABC1= θ, then cos θ is equal toa)1/5b)2/5c)2/√5d)4/5Correct answer is option 'B'. Can you explain this answer?, a detailed solution for A rectangle ABCD of dimensions r and 2r is folded along diagonal BD such that planes ABD and CBD are perpendicular to each other. Let the position of the vertex A remains unchanged and C1is the new position of C.If∠∠ABC1= θ, then cos θ is equal toa)1/5b)2/5c)2/√5d)4/5Correct answer is option 'B'. Can you explain this answer? has been provided alongside types of A rectangle ABCD of dimensions r and 2r is folded along diagonal BD such that planes ABD and CBD are perpendicular to each other. Let the position of the vertex A remains unchanged and C1is the new position of C.If∠∠ABC1= θ, then cos θ is equal toa)1/5b)2/5c)2/√5d)4/5Correct answer is option 'B'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A rectangle ABCD of dimensions r and 2r is folded along diagonal BD such that planes ABD and CBD are perpendicular to each other. Let the position of the vertex A remains unchanged and C1is the new position of C.If∠∠ABC1= θ, then cos θ is equal toa)1/5b)2/5c)2/√5d)4/5Correct answer is option 'B'. Can you explain this answer? tests, examples and also practice JEE tests.

|
Explore Courses for JEE exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
























