IIT JAM Exam > IIT JAM Questions > Molar heat capacity of water in equilibrium w...
Start Learning for Free
Molar heat capacity of water in equilibrium with ice at constant pressure is a)zero b)infinite c) 40.45J/K/mol d) 75.48J/K/mol .Correct answer is option C .Can you explain this answer?
Verified Answer
Molar heat capacity of water in equilibrium with ice at constant press...
Ans.
Method to Solve :

 This question is part of UPSC exam. View all IIT JAM courses
This question is part of UPSC exam. View all IIT JAM courses
Most Upvoted Answer
Molar heat capacity of water in equilibrium with ice at constant press...
Ans.
Method to Solve :
Heat capacity at constant pressure may be defined as the rate of change of enthalpy with temperature at constant pressure.
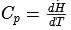
Since water and ice is at equilibrium, there is no change in temperature. They are at same temperature. So dT =0 and we know that something divided by 0 is infinity
Thus Cp= infinity ( at constant pressure)
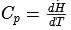
Since water and ice is at equilibrium, there is no change in temperature. They are at same temperature. So dT =0 and we know that something divided by 0 is infinity
Thus Cp= infinity ( at constant pressure)
Community Answer
Molar heat capacity of water in equilibrium with ice at constant press...
Molar heat capacity is the amount of heat required to raise the temperature of one mole of a substance by 1 Kelvin (or 1 degree Celsius). In this case, we are considering water in equilibrium with ice at constant pressure.
In equilibrium, the temperature remains constant, meaning that there is no change in the thermal energy of the system. Therefore, the molar heat capacity of water in equilibrium with ice is zero. This is because no heat is required to raise the temperature of the system since the temperature is constant.
However, it is important to note that the molar heat capacity of water in equilibrium with ice is not exactly zero. It is very close to zero but not exactly zero due to the small changes in temperature that may occur in the system.
The molar heat capacity of water in equilibrium with ice is approximately 40.45 J/K/mol. This value represents the heat capacity of water at very low temperatures, where the system is close to equilibrium.
The molar heat capacity of water at higher temperatures is different and is approximately 75.48 J/K/mol. This value represents the heat capacity of water when it is not in equilibrium with ice.
It is important to understand that the molar heat capacity of a substance can vary depending on the conditions under which it is measured. In this case, we are specifically considering water in equilibrium with ice at constant pressure.
In equilibrium, the temperature remains constant, meaning that there is no change in the thermal energy of the system. Therefore, the molar heat capacity of water in equilibrium with ice is zero. This is because no heat is required to raise the temperature of the system since the temperature is constant.
However, it is important to note that the molar heat capacity of water in equilibrium with ice is not exactly zero. It is very close to zero but not exactly zero due to the small changes in temperature that may occur in the system.
The molar heat capacity of water in equilibrium with ice is approximately 40.45 J/K/mol. This value represents the heat capacity of water at very low temperatures, where the system is close to equilibrium.
The molar heat capacity of water at higher temperatures is different and is approximately 75.48 J/K/mol. This value represents the heat capacity of water when it is not in equilibrium with ice.
It is important to understand that the molar heat capacity of a substance can vary depending on the conditions under which it is measured. In this case, we are specifically considering water in equilibrium with ice at constant pressure.

|
Explore Courses for IIT JAM exam
|

|
Similar IIT JAM Doubts
Molar heat capacity of water in equilibrium with ice at constant pressure is a)zero b)infinite c) 40.45J/K/mol d) 75.48J/K/mol .Correct answer is option C .Can you explain this answer?
Question Description
Molar heat capacity of water in equilibrium with ice at constant pressure is a)zero b)infinite c) 40.45J/K/mol d) 75.48J/K/mol .Correct answer is option C .Can you explain this answer? for IIT JAM 2024 is part of IIT JAM preparation. The Question and answers have been prepared according to the IIT JAM exam syllabus. Information about Molar heat capacity of water in equilibrium with ice at constant pressure is a)zero b)infinite c) 40.45J/K/mol d) 75.48J/K/mol .Correct answer is option C .Can you explain this answer? covers all topics & solutions for IIT JAM 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Molar heat capacity of water in equilibrium with ice at constant pressure is a)zero b)infinite c) 40.45J/K/mol d) 75.48J/K/mol .Correct answer is option C .Can you explain this answer?.
Molar heat capacity of water in equilibrium with ice at constant pressure is a)zero b)infinite c) 40.45J/K/mol d) 75.48J/K/mol .Correct answer is option C .Can you explain this answer? for IIT JAM 2024 is part of IIT JAM preparation. The Question and answers have been prepared according to the IIT JAM exam syllabus. Information about Molar heat capacity of water in equilibrium with ice at constant pressure is a)zero b)infinite c) 40.45J/K/mol d) 75.48J/K/mol .Correct answer is option C .Can you explain this answer? covers all topics & solutions for IIT JAM 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Molar heat capacity of water in equilibrium with ice at constant pressure is a)zero b)infinite c) 40.45J/K/mol d) 75.48J/K/mol .Correct answer is option C .Can you explain this answer?.
Solutions for Molar heat capacity of water in equilibrium with ice at constant pressure is a)zero b)infinite c) 40.45J/K/mol d) 75.48J/K/mol .Correct answer is option C .Can you explain this answer? in English & in Hindi are available as part of our courses for IIT JAM.
Download more important topics, notes, lectures and mock test series for IIT JAM Exam by signing up for free.
Here you can find the meaning of Molar heat capacity of water in equilibrium with ice at constant pressure is a)zero b)infinite c) 40.45J/K/mol d) 75.48J/K/mol .Correct answer is option C .Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Molar heat capacity of water in equilibrium with ice at constant pressure is a)zero b)infinite c) 40.45J/K/mol d) 75.48J/K/mol .Correct answer is option C .Can you explain this answer?, a detailed solution for Molar heat capacity of water in equilibrium with ice at constant pressure is a)zero b)infinite c) 40.45J/K/mol d) 75.48J/K/mol .Correct answer is option C .Can you explain this answer? has been provided alongside types of Molar heat capacity of water in equilibrium with ice at constant pressure is a)zero b)infinite c) 40.45J/K/mol d) 75.48J/K/mol .Correct answer is option C .Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Molar heat capacity of water in equilibrium with ice at constant pressure is a)zero b)infinite c) 40.45J/K/mol d) 75.48J/K/mol .Correct answer is option C .Can you explain this answer? tests, examples and also practice IIT JAM tests.

|
Explore Courses for IIT JAM exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.



















